| 题目名称 | 1452. [IOI 1999]纸牌问题 |
|---|---|
| 输入输出 | flat.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:4, 提交:9, 通过率:44.44% | ||||
|
|
100 | 0.103 s | 0.32 MiB | C++ |
|
|
100 | 0.113 s | 0.31 MiB | C++ |
|
|
100 | 0.149 s | 0.10 MiB | C++ |
|
|
100 | 0.154 s | 4.05 MiB | C++ |
|
|
30 | 0.057 s | 0.31 MiB | C++ |
|
|
0 | 0.091 s | 0.28 MiB | C++ |
|
|
0 | 0.096 s | 0.31 MiB | C++ |
|
|
0 | 0.102 s | 0.32 MiB | C++ |
|
|
0 | 6.004 s | 0.31 MiB | C++ |
| 本题关联比赛 | |||
| 2022级数学专题练习赛3 | |||
| 关于 纸牌问题 的近10条评论(全部评论) |
|---|
【题目描述】
这是一个均分纸牌的游戏。有 $N$ 列纸牌,每列有纸牌若干张(可能是零张),如图 $1$ 所示。纸牌列用从 $1$ 到 $N$ 的整数标号,$1$ 和 $N$ 分别是纸牌列两端的标号。在移动纸牌时你需要指定一个确定的列 $P$ 和一个确定的数字 $m$。而后从 $p$ 列上移动 $m$ 张纸牌到每一个相邻的列上,参见图 $2$.如果 $1<p<N$ 的话,则 $p$ 列有两个相邻的列,分别是 $p-1$ 和 $p+1$;如果 $p=1$ 的话,则只有一个相邻列,其列号为 $2$;如果 $P = N$ 的话,则只有一个相邻列,其列号为 $N-1$。
注意,如果 $p$ 列有两个相邻的列.则进行上述移动时,$p$ 列至少要有 $2m$ 张纸牌;如果 $p$ 列只有一个相邻的列,则进行这样的移动时 $p$ 列就需要至少 $m$ 张纸牌。
这个游戏的目的是”均分”所有的纸牌列,使每列都有相同的纸牌数,而且用最少的移动达到这一目的。假定有超过一种符合上述要求的移动方法,你只需给出其中一种。
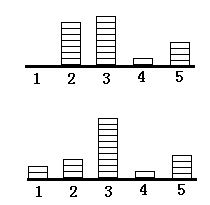
图 $1$.五列纸牌,分别有 $0$:$7$,$8$,$1$,$4$ 张纸牌
图2.图 $1$ 的纸牌列在执行完移动 $P = 2$ ,$m = 2$ 后的状态
$Ø$ 假设条件
$u$ 最大的移动次数保证不多于 $10,000$ 次。
$u$ $2 ≤ N ≤ 200$。
$u$ $0 ≤ C_i ≤ 2000$,在这里 $C_i$ 是游戏开始时第 $i$ 列的纸牌数$(1 ≤ I ≤ N)$。
【输入格式】
输入有两行。
第一行是纸牌的总列数 $N$;
第二行有 $N$ 个整数,其中第 $i$ 个数是 $C_i$ 的值。
【输出格式】
第一行是移动的次数(称为 $M$)。
以下 $M$ 行每行包含两个整数,分别表示移动中的 $p$ 和 $m$。
移动的输出次序必须和移动的执行次序相同。因此,第一次移动应该写在输出文件的第二行上。
【输入输出样例】
flat.in : 5 0 7 8 1 4 flat.out: 5 5 2 3 4 2 4 3 1 4 2
【提示】
对于每个测试点,你的得分将由如下规则给出:
若你给出的操作序列不能均分纸牌,那么你在这个测试点得 $0$ 分。
假设这个测试点的分值是 $A$,你的答案步数是 $x$,而标准答案的步数是 $B$。
你的得分为:
$A$ $if$ $x \leq B$
$2A(1.5B - x) / B$ $if$ $B < x < 1.5B$
$0$ $if$ $x \geq 1.5B$
【来源】
$IOI1999$