| 题目名称 | 3610. [Nescafe 26]Rainbow的信号 |
|---|---|
| 输入输出 | signal.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:0, 通过率:0% | |||
| 关于 Rainbow的信号 的近10条评论(全部评论) |
|---|
【题目描述】
Freda 发明了传呼机之后,rainbow 进一步改进了传呼机发送信息所使用的信号。由于现在是数字、信息时代,rainbow 发明的信号用$n$个自然数表示。为了避免两个人的对话被大坏蛋 VariantF 偷听,rainbow 把对话分成A、B、C三部分,分别用a、b、c三个密码加密。现在 Freda 接到了 rainbow 的信息,她的首要工作就是解密。Freda 了解到,这三部分的密码计算方式如下:
在$1\sim n$这$n$个数中,等概率地选取两个数$l,r$,如果$l>r$,则交换$l,r$。
把信号中的第$l$个数到第$r$个数取出来,构成一个数列$P$。
A部分对话的密码是数列$P$的xor和的数学期望值,xor和就是数列$P$中各个数异或之后得到的数;xor和的期望就是对于所有可能选取的$l,r$,所得到的数列的xor和的平均数。
B部分对话的密码是数列$P$的and和的期望,定义类似于xor和。
C部分对话的密码是数列$P$的or和的期望,定义类似于xor和。
请你帮忙计算这三个密码。
【输入格式】
第一行一个正整数$n$。
第二行$n$个自然数,表示 Freda 接到的信号。
【输出格式】
一行三个实数,分别表示xor和、and和、or和的期望,四舍五入保留3位小数,相邻两个实数之间用一个空格隔开。
【样例输入1】
2 4 5
【样例输出1】
2.750 4.250 4.750
【样例输入2】
3 1 0 1
【样例输出2】
0.667 0.222 0.889
【样例解释】
样例1共包含四种可能的$l,r$:
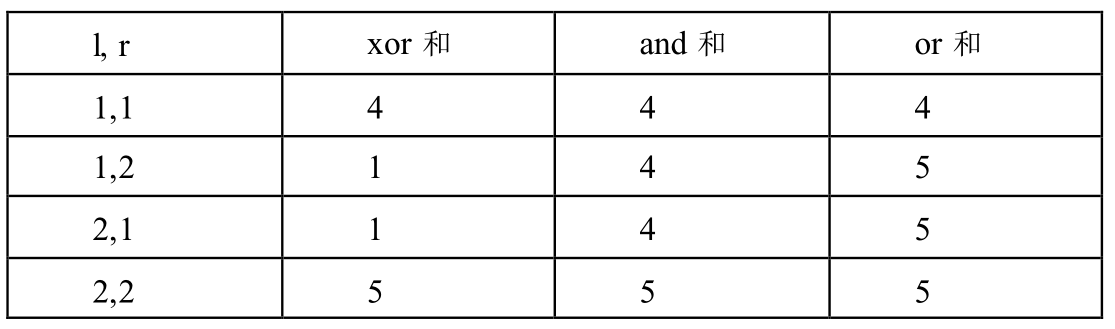
以上没一对$l,r$出现的概率均相同,因此分别对 xor 和、and 和、or 和取平均数就是数学期望值。
【数据规模与约定】
对于20%的数据,$1\leq n\leq 100$。
对于40%的数据,$1\leq n\leq 1000$。
对于另外30%的数据,$n$个数为0或1。
对于100%的数据,$1\leq n\leq 10^5$,n个自然数均不超过$10^9$。