| 题目名称 | 3446. [CTSC 2020]猜数游戏 |
|---|---|
| 输入输出 | gamed.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:0, 通过率:0% | |||
| 关于 猜数游戏 的近10条评论(全部评论) |
|---|
【题目描述】
黑板上写有 $n$ 个互不相等且都小于 $p$ 的正整数 $a_1,a_2,…,a_n$。小 $J$ 想用这些数字和小 $M$ 玩一个猜数游戏。
游戏规则十分简单:游戏开始时,小 $J$ 会从这些数字中随机选择若干个让小 $M$ 来猜,而小 $M$ 则可以通过若干次询问来确定小 $J$ 选择了哪些数字。
每一次询问的模式如下:小 $M$ 可以任意指定一个数字 $a_k$,若它是小 $J$ 所选择的数字之一,则小 $J$ 会告诉小 $M$ 他所选择的数字中所有能表示成 $(a_k)^m\ mod\ p$ 的数,其中 $m$ 是任意正整数,$mod$ 表示求二者做带余除法后的余数。反之,若 $a_k$ 没有被小 $J$ 选中,则小 $J$ 只会告诉小$M$ $a_k$ 没有被选中。
游戏会在小 $M$ 确定小 $J$ 所选中的所有数字后立刻结束。
例如,若 $n=4,p=7$,数字 ${a_n}$ 按下标顺序依次为 ${1,3,4,6}$,小 $J$ 选定的数字为 ${1,4,6}$,一种可能的游戏进行的过程(并非是最优过程)如下:

$3$ 次询问后小 $J$ 所选出的所有数都已被小 $M$ 确定,游戏结束。
小 $M$ 还有作业没有写完,因此他需要对游戏进行的时间进行评估。他想知道为了使游戏结束,他所需要做出询问的最小次数的期望 $S$ 是多少。
为了避免精度误差,你需要输出答案乘 $(2^n-1)$ 后模 $998244353$ 的余数。在本题中,你可以认为小 $J$ 每次在选数时会在集合 ${a_1,a_2,…,a_n}$ 的全部非空子集中等概率地选择一个,在这个前提下可以证明 $(2^n-1)×S$ 一定是一个整数。
【输入格式】
第一行两个正整数 $n$ 和 $p$。
第二行 $n$ 个正整数,依次表示 $a_1,a_2,…,a_n$。
【输出格式】
一行一个整数表示答案。
【样例1输入】
4 7 1 3 4 6
【样例1输出】
17
【样例1解释】
下表给出了小 $J$ 所选的子集与小 $M$ 最小询问次数的关系:

因此最小询问的期望 $S = 17/15$
【样例2输入】
8 9 1 2 3 4 5 6 7 8
【样例2输出】
532
【全部样例输入输出】
点击下载所有样例
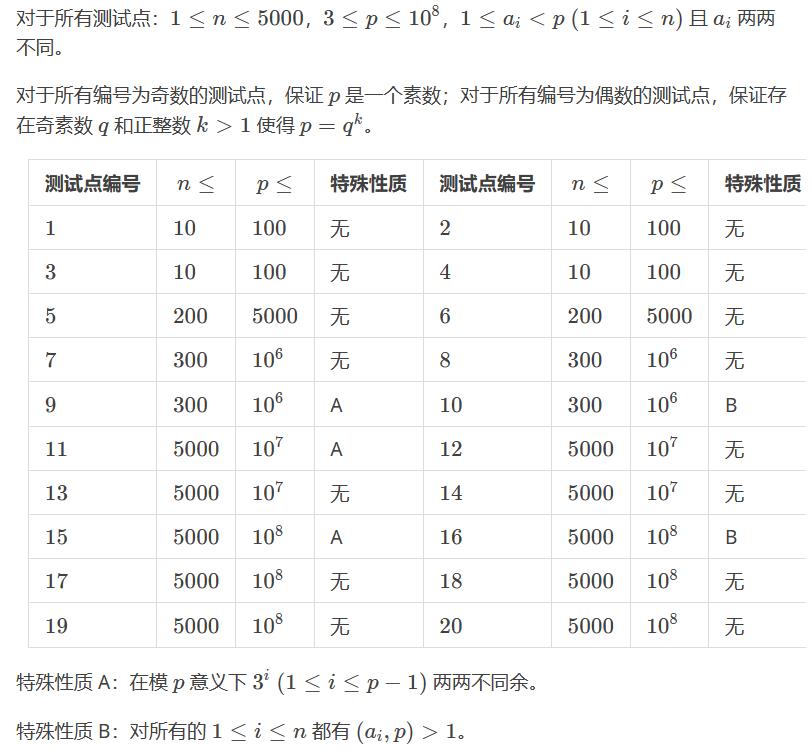
【数据规模】