| 题目名称 | 2936. [HAOI 2018]反色游戏 |
|---|---|
| 输入输出 | game.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 查看题解 | 分享题解 |
| 通过:3, 提交:5, 通过率:60% | ||||
|
|
100 | 0.530 s | 10.50 MiB | C++ |
|
|
100 | 0.671 s | 5.21 MiB | C++ |
|
|
100 | 0.760 s | 5.75 MiB | C++ |
|
|
10 | 0.549 s | 10.50 MiB | C++ |
|
|
0 | 0.545 s | 10.50 MiB | C++ |
| 本题关联比赛 | |||
| HAOI 2018 Day1 | |||
| 关于 反色游戏 的近10条评论(全部评论) |
|---|
【题目描述】
小 C 和小 G 经常在一起研究博弈论问题,有一天他们想到了这样一个游戏。
有一个 $n$ 个点 $m$ 条边的无向图,初始时每个节点有一个颜色,要么是黑色,要么是白色。现在他们对于每条边做出一次抉择:要么将这条边连接的两个节点都反色(黑变白,白变黑),要么不作处理。他们想把所有节点都变为白色,他们想知道在 $2^m$ 种决策中,有多少种方案能达成这个目标。
小 G 认为这个问题太水了,于是他还想知道,对于第 $i$ 个点,在删去这个点及与它相连的边后,新的答案是多少。
由于答案可能很大,你只需要输出答案对 $10^9+7$ 取模后的结果.
【输入格式】
第一行一个整数 $T$,表示数据组数.
每组数据第一行两个整数 $n, m$,表示点数和边数.
接下来 $m$ 行,每行两个整数 $u, v$,描述无向图的一条边.
接下来一行一个长度为 $n$ 的 $0/1$ 串,如果第 $i$ 个字符为 $0$ 表示第 $i$ 个点为白色,否则为黑色。
【输出格式】
每组数据输出一行 $n+1$ 个整数,第一个整数表示不删去任何点时的答案。接下来 $n$ 个整数,第 $i$ 个表示删去第 $i$ 个点时的答案。
【输入样例】
2 5 5 1 2 2 3 3 4 2 4 3 5 00000 5 4 1 2 2 3 2 4 2 5 11111
【输出样例】
2 2 1 1 1 2 0 1 0 1 1 1
【样例解释】
第一组数据,在不删掉任何点时,有两种方案:要么对所有的边都不做操作;要么对 (2, 3), (3, 4), (2, 4) 做操作.
在删掉 2 号点或 3 号点或 4 号点时,唯一的方案是对所有边都不做操作.注意图可能不连通
【数据范围与约定】
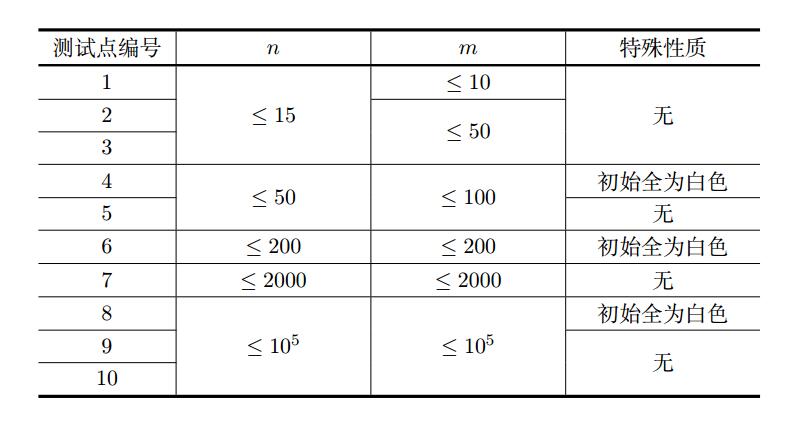
对于所有数据,有$1\leq T\leq 5,1\leq n,m\leq 10^5,1\leq u,v\leq n$,没有重边和自环。