| 题目名称 | 1501. [UVa 1356] 桥上的绳索 |
|---|---|
| 输入输出 | bridge.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:5, 提交:16, 通过率:31.25% | ||||
|
|
100 | 0.059 s | 0.29 MiB | C++ |
|
|
100 | 0.060 s | 0.29 MiB | C++ |
|
|
100 | 0.073 s | 0.29 MiB | C++ |
|
|
100 | 0.076 s | 0.32 MiB | C++ |
|
|
100 | 0.079 s | 0.31 MiB | C++ |
|
|
90 | 0.052 s | 0.29 MiB | C++ |
|
|
0 | 0.000 s | 0.29 MiB | C++ |
|
|
0 | 0.001 s | 0.29 MiB | C++ |
|
|
0 | 0.001 s | 0.29 MiB | C++ |
|
|
0 | 0.043 s | 0.29 MiB | C++ |
| 关于 桥上的绳索 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
这题数据是怎么回事口牙。。怎么输入文件还有字母。
2017-03-09 20:25
3楼
| ||||
|
Simpson真是好用
2014-01-29 11:38
2楼
| ||||
|
可以硬解……或者数值积分……即Simpson公式法
| ||||
【题目描述】
悬索桥凭借钢缆悬在空中,这些巨大的钢缆从桥的一头延伸到另一头。钢缆被固定在高塔上,两端用锚碇钉牢。这些塔使得钢缆能够延伸漫长的距离。
假设两座相邻塔间的最大距离是D,从塔顶到桥面的距离是H。同时假设所有两座相邻塔间的钢缆形状都是同样的对称抛物线(如图所示)。现在给出桥长B,钢缆总长,假设塔的数量尽可能少,要求你计算钢缆最低点到桥面的距离(假定桥的两端各建了一座塔)。
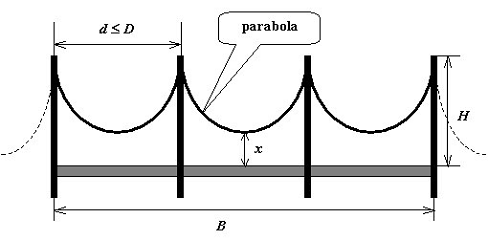
【输入格式】
输入包含多组数据。
输入文件的第一行是一个正整数T(1<=T<=10),代表数据组数。
下面是T组数据。
每组数据占一行,包含4个正整数:
D——两塔之间的最大距离
H——塔顶到桥面的距离
B——桥长
L——钢缆总长
数据保证B<=L,钢缆总是悬在路的上方。
【输出格式】
具体格式见样例。
对每组数据,先输出一行"Case #:",其中#是数据组数,从1开始编号。
对每组数据,输出桥面到钢缆最低点的距离。保留两位小数。
【样例输入】
2 20 101 400 4042 1 2 3 4
【样例输出】
Case 1: 1.00 Case 2: 1.60
【提示】
使用“保留2位小数”的指令,假设计算机能正确舍入。
【来源】
刘汝佳,《算法竞赛入门经典训练指南》表2-14