| 题目名称 | 2905. [WC 2018] 州区划分 |
|---|---|
| 输入输出 | walkk.in/out |
| 难度等级 | ★★★★☆ |
| 时间限制 | 5000 ms (5 s) |
| 内存限制 | 1024 MiB |
| 测试数据 | 15 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:5, 通过率:0% | ||||
|
|
0 | 0.000 s | 0.00 MiB | C++ |
|
|
0 | 0.013 s | 401.24 MiB | C++ |
|
|
0 | 91.982 s | 368.32 MiB | C++ |
|
|
0 | 134.721 s | 319.64 MiB | C++ |
|
|
0 | 150.525 s | 501.54 MiB | C++ |
| 关于 州区划分 的近10条评论(全部评论) |
|---|
【题目描述】
小 S 现在拥有 n 座城市,第 i 座城市的人口为 w i,城市与城市之间可能有双向道路相连。
现在小 S 要将这 n 座城市划分成若干个州,每个州由至少一个城市组成,每个城市在恰好一个州内。
假设小 S 将这些城市划分成了 k 个州,设 V i 是第 i 个州包含的所有城市组成的集合。定义一条道路是一个州的内部道路,当且仅当这条道路的两个端点城市都在这个州内。如果一个州内部存在一条起点终点相同,不经过任何不属于这个州的城市,且经过这个州的所有内部道路都恰好一次的路径(路径长度可以为 0),则称这个州是不合法的。
定义第 i 个州的满意度为:第 i 个州的人口在前 i 个州的人口中所占比例的 p 次幂,即:
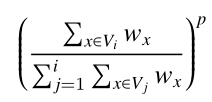
定义一个划分的满意度为所有州的满意度的乘积。
求所有合法的划分方案的满意度之和。
答案对 998244353 取模。
两个划分 {V 1 ...V k } 和 {C 1 ...C s } 是不同的,当且仅当 k≠s,或存在某个 1 ≤ i ≤ k,使得 V i≠ C i 。
【输入格式】
输入第一行包含三个整数 n,m, p,表示城市个数、城市之间的道路个数以及题目描述中的常数 p;
接下来 m 行,每行两个正整数 u,v,描述一条无向的道路,保证无重边无自环;
输入第 m + 2 行有 n 个正整数,第 i 个正整数表示 w i 。
【输出格式】
输出一行一个整数表示答案在模 998244353 意义下的取值。
即设答案化为最简分式后的形式为a/b,其中 a 和 b 互质。输出整数 x 使得 bx ≡ amod 998244353 且 0 ≤ x < 998244353。可以证明这样的整数 x 是唯一的。
【样例输入】
3 2 1
1 2
2 3
1 1 1
【样例输出】
1
【提示】
x^p−1 ≡ 1 mod p,其中 p 为质数,x ∈ [1, p)。
【子任务】
保证对于所有数据有:0 ≤ n ≤ 21,0 ≤ m ≤n∗(n−1)/2,0 ≤ p ≤ 2,1 ≤ w i ≤ 100。

【来源】
WC2018T2