| 题目名称 | 4199. [CSP-S 2025 T4]员工招聘 |
|---|---|
| 输入输出 | employ.in/out |
| 难度等级 | ★★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:7, 提交:16, 通过率:43.75% | ||||
|
|
100 | 1.377 s | 4.62 MiB | C++ |
|
|
100 | 3.789 s | 7.81 MiB | C++ |
|
|
100 | 3.822 s | 10.10 MiB | C++ |
|
|
100 | 4.327 s | 7.82 MiB | C++ |
|
|
100 | 4.938 s | 6.10 MiB | C++ |
|
|
100 | 7.544 s | 149.87 MiB | C++ |
|
|
100 | 8.104 s | 7.56 MiB | C++ |
|
|
20 | 15.901 s | 92.40 MiB | C++ |
|
|
20 | 15.918 s | 94.47 MiB | C++ |
|
|
8 | 15.718 s | 79.58 MiB | C++ |
| 关于 员工招聘 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
滚动三维数组
| ||||
|
111
| ||||
【题目描述】
小 Z 和小 H 想要合伙开一家公司,共有 $n$ 人前来应聘,编号为 $1 \sim n$。小 Z 和小 H 希望录用至少 $m$ 人。
小 H 是面试官,将在接下来 $n$ 天每天面试一个人。小 Z 负责决定应聘人前来面试的顺序。具体地,小 Z 可以选择一个 $1 \sim n$ 的排列 $p$,然后在第 $i$ ($1 \leq i \leq n$) 天通知编号为 $p_i$ 的人前来面试。
小 H 准备了 $n$ 套难度不一的面试题。由于 $n$ 个前来应聘的人水平大致相同,因此对于同一套题,所有人的作答结果是一致的。具体地,第 $i$ ($1 \leq i \leq n$) 天的面试题的难度为 $s_i \in \{0,1\}$,其中 $s_i = 0$ 表示这套题的难度较高,没有人能够做出;$s_i = 1$ 表示这套题的难度较低,所有人都能做出。小 H 会根据面试者的作答结果决定是否录用,即如果面试者没有做出面试题,则会拒绝,否则会录用。
然而,每个人的耐心都有一定的上限,如果在他面试之前未录用的人数过多,则他会直接放弃参加面试。具体地,编号为 $i$ ($1 \leq i \leq n$) 的人的耐心上限可以用非负整数 $c_i$ 描述,若在他之前已经有不少于 $c_i$ 人被拒绝或放弃参加面试,则他也将放弃参加面试。
小 Z 想知道一共有多少种面试的顺序 $p$ 能够让他们录用至少 $m$ 人。你需要帮助小 Z 求出,能够录用至少 $m$ 人的排列 $p$ 的数量。由于答案可能较大,你只需要求出答案对 $998\,244\,353$ 取模后的结果。
【输入格式】
输入的第一行包含两个正整数 $n, m$,分别表示前来应聘的人数和希望录用的人数。
输入的第二行包含一个长度为 $n$ 的字符串 $s_1 \dots s_n$,表示每一天的面试题的难度。
输入的第三行包含 $n$ 个非负整数 $c_1, c_2, \dots, c_n$,表示每个人的耐心上限。
【输出格式】
输出一行一个非负整数,表示能够录用至少 $m$ 人的排列 $p$ 的数量对 $998\,244\,353$ 取模后的结果。
【样例1输入】
3 2 101 1 1 2
【样例1输出】
2
【样例1说明】
共有以下 2 种面试的顺序 $p$ 能够让小 Z 和小 H 录用至少 2 人:
1. $p = [1,2,3]$, 依次录用编号为 1 的人和编号为 3 的人;
2. $p = [2,1,3]$, 依次录用编号为 2 的人和编号为 3 的人。
【样例2输入】
10 5 1101111011 6 0 4 2 1 2 5 4 3 3
【样例2输出】
2204128
【样例3,4,5】
样例3满足测试点 6 ~ 8 的约束条件。
样例4满足测试点 12 ~ 14 的约束条件。
样例5满足测试点 18 ~ 21 的约束条件。
【数据规模与约定】
对于所有测试数据,保证:
- $1 \leq m \leq n \leq 500$;
- 对于所有 $1 \leq i \leq n$,均有 $s_i \in \{0,1\}$;
- 对于所有 $1 \leq i \leq n$,均有 $0 \leq c_i \leq n$。
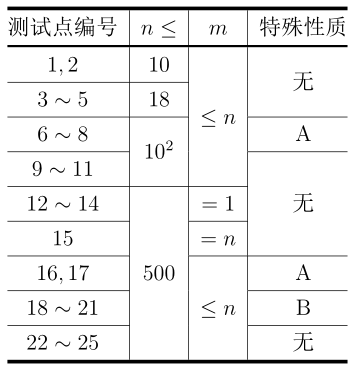
特殊性质 A: 对于所有 $1 \leq i \leq n$,均有 $s_i = 1$。
特殊性质 B: 在 $s_1, s_2, \dots, s_n$ 中最多只有 18 个取值为 1,即 $\sum_{i=1}^{n} s_i \leq 18$。