| 题目名称 | 3895. [桐柏一中邀请赛S13]焰硝庭火 |
|---|---|
| 输入输出 | firework.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:1, 通过率:100% | ||||
|
|
100 | 0.276 s | 2.67 MiB | C++ |
| 关于 焰硝庭火 的近10条评论(全部评论) |
|---|
【题目描述】
Yoimiya 给了你一个长度为 $n$ 的非负整数序列 $a$,她定义一次操作是选择一个区间 $[l,r]$,并将区间中的所有 $a_i$ 都减去 $1$。
现在她想要把序列中的所有数都变成 $0$。她认为一次操作若选择了区间 $[l,r]$,其代价为 $(r − l + 1)^2$ 。
Yoimiya 想要求出,在最小化操作次数的前提下,把所有数变成 $0$ 所需要进行的操作的代价之和的最小值和最大值分别是多少。
【输入格式】
第一行一个正整数 $n$ 表示序列长度。
第二行 $n$ 个非负整数 $a_1,a_2,\cdots,a_n$ ,表示 Yoimiya 给你的序列。
【输出格式】
输出一行两个非负整数表示答案。
【样例输入1】
4 1 1 1 1
【样例输出1】
16 16
【样例1说明】
要使操作次数最小,唯一的方案是进行一次操作并选择区间 $[1,4]$,代价为 $16$。
【样例输入2】
6 1 1 4 5 1 4
【样例输出2】
40 52
【样例2说明】
至少需要 $8$ 次操作才能使整个序列都变成 $0$。
使得代价最小化的一种操作方案为:分别选取区间 $[3,4],[6,6],[3,4],[4,6],[1,4],[6,6],[3,4],[6,6]$,总代价为 $2^2 + 1^2 + 2^2 + 3^2 + 4^2 + 1^2 + 2^2 + 1^2 = 40$。
使得代价最大化的一种操作方案为:分别选取区间 $[3,4],[6,6],[3,4],[1,6],[4,4],[6,6],[3,4],[6,6]$,总代价为 $2^2 + 1^2 + 2^2 + 6^2 + 1^2 + 1^2 + 2^2 + 1^2 = 52$。
【样例3/4下载】
【数据规模与约定】
对于所有测试点:$1 ≤ n ≤ 10^6 ,0 ≤ a_i ≤ 10^6$ 。
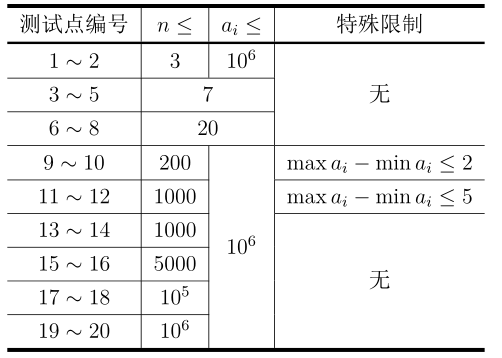
每个测试点的具体限制见下表: