| 题目名称 | 3581. [统一省选 2021]图函数 |
|---|---|
| 输入输出 | graph.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 查看题解 | 分享题解 |
| 通过:2, 提交:10, 通过率:20% | ||||
|
|
100 | 1.095 s | 4.91 MiB | C++ |
|
|
100 | 8.044 s | 6.24 MiB | C++ |
|
|
80 | 9.940 s | 6.24 MiB | C++ |
|
|
44 | 14.015 s | 9.37 MiB | C++ |
|
|
16 | 19.177 s | 2.89 MiB | C++ |
|
|
8 | 2.023 s | 2.85 MiB | C++ |
|
|
8 | 8.268 s | 4.11 MiB | C++ |
|
|
8 | 21.000 s | 8.05 MiB | C++ |
|
|
0 | 0.000 s | 0.00 MiB | C++ |
|
|
0 | 4.876 s | 3.17 MiB | C++ |
| 本题关联比赛 | |||
| HAOI2021 Day1 | |||
| 关于 图函数 的近10条评论(全部评论) |
|---|
【题目描述】
对于一张 $n$ 个点 $m$ 条边的有向图 $G$(顶点从 $1\sim n$编号),定义函数 $f(u,G)$:
1. 初始化返回值 $cnt = 0$,图 $G'= G$。
2. 从 $1$ 至 $n$ 按顺序枚举顶点 $v$,如果当前的图$G'$中,从 $u$ 到 $v$ 与从 $v$ 到 $u$ 的路径都存在,则将 $cnt + 1$,并在图$G''$中删去顶点 $v$ 以及与它相关的边。
3. 第 2 步结束后,返回值 $cnt$ 即为函数值。
现在给定一张有向图 $G$,请你求出$h(G) = f(1,G) + f(2,G) + \cdots + f(n,G)$ 的值。
更进一步地,记删除(按输入顺序给出的)第 $1\sim i$条边后的图为$G_i(1\leq i\leq m)$,请你求出所有 $h(G_i)$ 的值。
【输入格式】
第一行两个整数 $n,m$ 表示图的点数与边数。
接下来 $m$ 行每行两个整数,第 $i$ 行的两个整数 $x_i ,y_i$ 表示一条有向边$x_i\rightarrow y_i$ 。
数据保证$x_i\neq y_i$且同一条边不会给出多次。
【输出格式】
输出一行 $m + 1$ 个整数,其中第一个数表示给出的完整图 $G$的 $h(G)$ 值。第 $i(2\leq i\leq m+1)$个整数表示$h(G_{i-1})$。
【样例输入1】
4 6 2 3 3 2 4 1 1 4 2 1 3 1
【样例输出1】
6 5 5 4 4 4 4
【样例1说明】
对于给出的完整图$ G$:
1. $f(1,G) = 1$,过程中删除了顶点 1。
2. $f(2,G) = 1$,过程中删除了顶点 2。
3. $f(3,G) = 2$,过程中删除了顶点 2,3。
4. $f(4,G) = 2$,过程中删除了顶点 1,4。
【输入输出样例2】
【数据规模与约定】
对于所有测试数据:$2\leq n\leq 1000,1\leq m\leq 2\times 10^5,1\leq x_i,y_i\leq n$。
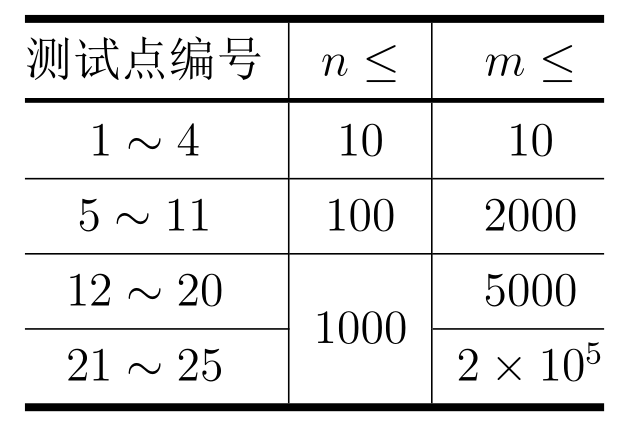
每个测试点的具体限制见下表:
【来源】
2021统一省选A卷 Day1 Task3