关于方格取数的近10条评论(全部评论)
#转自ChatGPT 5-high 对于方格取数问题，定义状态 $dp[j][i]$ 表示走到第 $j$ 列第 $i$ 行时能获得的最大和。 ## 初始条件 $$dp[0][0] = a[0][0]$$ $$dp[0][i] = dp[0][i-1] + a[i][0], \quad 1 \leq i < n$$ ## 状态转移方程 $$dp[j][i] = \max_{0 \leq k < n} \left(dp[j-1][k] + \sum_{l=\min(i,k)}^{\max(i,k)} a[l][j]\right), \quad 1 \leq j < m, 0 \leq i < n$$ ## 最终答案 $$answer = dp[m-1][n-1]$$ 其中： - $n$ 为行数，$m$ 为列数 - $a[i][j]$ 表示第 $i$ 行第 $j$ 列的值 - $\min(i,k)$ 和 $\max(i,k)$ 分别表示 $i$ 和 $k$ 中的较小值和较大值 - 求和项表示在第 $j$ 列中从第 $k$ 行走到第 $i$ 行所经过的所有格子的值之和金牌教师王艳芳 2025-09-17 22:12 5楼
666，我还以为是个搜索，要不然记忆化要不然剪枝，结果你告诉我是dp？改了半天搜索就30分结果回家一问chatgpt是动规？金牌教师王艳芳 2025-09-16 22:52 4楼
/ - * 123 789+ 456 456+ 789 123 00 . 黑猪刘畅 2021-09-19 09:41 3楼
回复 @232623 : 留念...... ZooxTark➲ 2021-03-31 19:07 2楼
CSP2020纪念ムラサメ 2020-11-16 18:49 1楼

3501. [CSP 2020J]方格取数

★★☆ 输入文件：csp2020pj_number.in 输出文件：csp2020pj_number.out 简单对比
时间限制：1 s 内存限制：256 MiB

设有 $n\times m$ 的方格图，每个方格中都有一个整数。现有一只小熊，想从图的左上角走到右下角，每一步只能向上、向下或向右走一格，并且不能重复经过已经走过的方格，也不能走出边界。小熊会取走所有经过的方格中的整数，求它能取到的整数之和的最大值。

第 1 行两个正整数 $n,m$。

接下来 $n$ 行每行 $m$ 个整数，依次代表每个方格中的整数。

一个整数，表示小熊能取到的整数之和的最大值。

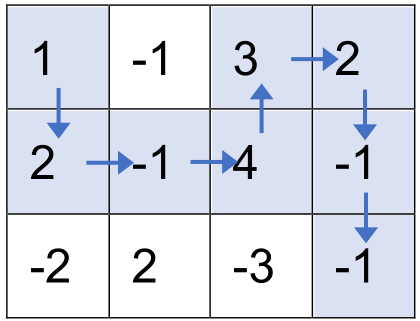
按上述走法，取到的数之和为 1 +2 + (-1) + 4 + 3 + 2 + (-1) + (-1) = 9，可以证明为最大值。

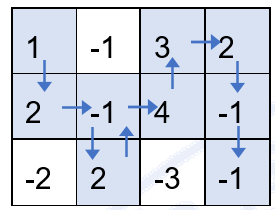
注意，上述走法是错误的，因为第 2 行第 2 列的方格走过了两次，而根据题意，不能重复经过已经走过的方格。

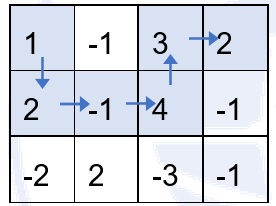
另外，上述走法也是错误的，因为没有走到右下角的终点。

2 5  
-1 -1 -3 -2 -7 
-2 -1 -4 -1 -2

-10

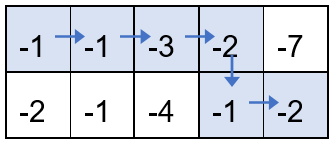
按上述走法，取到的数之和为(-1)+ (-1) + (-3) + (-2) + (-1) + (-2) = -10，可以证明为最大值。因此，请注意，取到的数之和的最大值也可能是负数。

对于 20% 的数据，$n,m\leq 5$。

对于 40% 的数据，$n,m\leq 50$。

对于 70% 的数据，$n,m\leq 300$。

对于 100% 的数据，$1\leq n,m\leq 1000$。方格中整数的绝对值不超过$10^4$。

CSP 2020PJ Task 4