| 题目名称 | 3465. [NOI 2020]美食家 |
|---|---|
| 输入输出 | delicacy.in/out |
| 难度等级 | ★★★★ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:1, 通过率:100% | ||||
|
|
100 | 5.194 s | 21.63 MiB | C++ |
| 关于 美食家 的近10条评论(全部评论) |
|---|
【题目描述】
坐落在 $Bzeroth$ 大陆上的精灵王国击退地灾军团的入侵后,经过十余年的休养生息,重新成为了一片欣欣向荣的乐土,吸引着八方游客。小 $W$ 是一位游历过世界各地的著名美食家,现在也慕名来到了精灵王国。
精灵王国共有 $n$ 座城市,城市从 $1$ 到 $n$ 编号,其中城市 $i$ 的美食能为小 $W$ 提供 $c_i$ 的愉悦值。精灵王国的城市通过 $m$ 条单向道路连接,道路从 $1$ 到 $m$ 编号,其中道路 $i$ 的起点为城市 $u_i$ ,终点为城市 $v_i$,沿它通行需要花费 $w_i$ 天。也就是说,若小 $W$ 在第 $d$ 天从城市 $u_i$ 沿道路 $i$ 通行,那么他会在第 $d+w_i$ 天到达城市 $v_i$。
小 $W$ 计划在精灵王国进行一场为期 $T$ 天的旅行,更具体地:他会在第 $0$ 天从城市 $1$ 出发,经过 $T$ 天的旅行,最终在恰好第 $T$ 天回到城市 $1$ 结束旅行。由于小 $W$ 是一位美食家,每当他到达一座城市时(包括第 $0$ 天和第 $T$ 天的城市 $1$),他都会品尝该城市的美食并获得其所提供的愉悦值,若小 $W$ 多次到达同一座城市,他将获得多次愉悦值。注意旅行途中小 $W$ 不能在任何城市停留,即当他到达一座城市且还未结束旅行时,他当天必须立即从该城市出发前往其他城市。

对于上图,小 $W$ 一种为期 $11$ 天的可行旅游方案为 $1→2→1→2→3→1$:
第 $0$ 天,小 $W$ 从城市 $1$ 开始旅行,获得愉悦值 $1$ 并向城市 $2$ 出发。
第 $1$ 天,小 $W$ 到达城市 $2$,获得愉悦值 $3$ 并向城市 $1$ 出发。
第 $4$ 天,小 $W$ 到达城市 $1$,获得愉悦值 $1$ 并向城市 $2$ 出发。
第 $5$ 天,小 $W$ 到达城市 $2$,获得愉悦值 $3$ 并向城市 $3$ 出发。
第 $7$ 天,小 $W$ 到达城市 $3$,获得愉悦值 $4$ 并向城市 $1$ 出发。
第 $11$ 天,小 $W$ 到达城市 $1$,获得愉悦值 $1$ 并结束旅行。
小 $W$ 在该旅行中获得的愉悦值之和为 $13$。
此外,精灵王国会在不同的时间举办 $k$ 次美食节。具体来说,第 $i$ 次美食节将于第 $t_i$ 天在城市 $x_i$ 举办,若小 $W$ 第 $t_i$ 天时恰好在城市 $x_i$,那么他在品尝城市 $x_i$ 的美食时会额外得到 $y_i$ 的愉悦值。现在小 $W$ 想请作为精灵王国接待使者的你帮他算出,他在旅行中能获得的愉悦值之和的最大值。
【输入格式】
第一行四个整数 $n,m,T,k$,依次表示城市数、道路条数、旅行天数与美食节次数。
第二行 $n$ 个整数 $c_i$,表示每座城市的美食所能提供的愉悦值。
接下来 $m$ 行每行三个整数 $u_i,v_i,w_i$,依次表示每条道路的起点、终点与通行天数。
最后 $k$ 行每行三个整数 $t_i,x_i,y_i$,依次表示每次美食节的举办时间、举办城市与提供的额外愉悦值。
本题中数据保证:
对所有 $1 ≤ i ≤ m$,有 $u_i ≠ v_i$。但数据中可能存在路线重复的单向道路,即可能存在 $1≤i<j≤m$,使得 $u_i = u_j,v_i = v_j$。
对每座城市都满足:至少存在一条以该该城市为起点的单向道路。
每次美食节的举办时间 $t_i$ 互不相同。
【输出格式】
仅一行一个整数,表示小 $W$ 通过旅行能获得的愉悦值之和的最大值。
若小 $W$ 无法在第 $T$ 天回到城市 $1$,则输出 $−1$。
【样例输入1】
3 4 11 0 1 3 4 1 2 1 2 1 3 2 3 2 3 1 4
【样例输出1】
13
【样例1解释】
该样例为题目描述中的例子,最优旅行方案见题目描述。
【样例输入2】
4 8 16 3 3 1 2 4 1 2 1 1 3 1 1 3 2 3 4 3 2 3 2 3 2 1 4 2 1 4 1 5 3 3 5 1 2 5 5 4 20
【样例输出2】
39
【样例2解释】
最优方案为 $1→3→4→2→3→4→1$。
第 $0$ 天,小 $W$ 从城市 $1$ 开始旅行,获得愉悦值 $3$ 并沿道路 $3$ 通行。
第 $2$ 天,小 $W$ 到达城市 $3$,获得愉悦值 $2$ 并沿道路 $4$ 通行。
第 $5$ 天,小 $W$ 到达城市 $4$,由于美食节获得愉悦值 $20+4$ 并沿道路 $7$ 通行。
第 $6$ 天,小 $W$ 到达城市 $2$,获得愉悦值 $1$ 并沿道路 $5$ 通行。
第 $8$ 天,小 $W$ 到达城市 $3$,获得愉悦值 $2$ 并沿道路 $4$ 通行。
第 $11$ 天,小 $W$ 到达城市 $4$,获得愉悦值 $4$ 并沿道路 $8$ 通行。
第 $16$ 天,小 $W$ 到达城市 $1$,获得愉悦值 $3$ 并结束旅行。
小 $W$ 获得的愉悦值之和为 $39$。
【数据范围】
对于所有测试点:
$1≤n≤50,n≤m≤501,0≤k≤200,1≤ti≤T≤10^9$。
$1≤w_i≤5,1≤c_i≤52501,1≤u_i,v_i,x_i≤n,1≤y_i≤10^9$。
每个测试点的具体限制见下表:
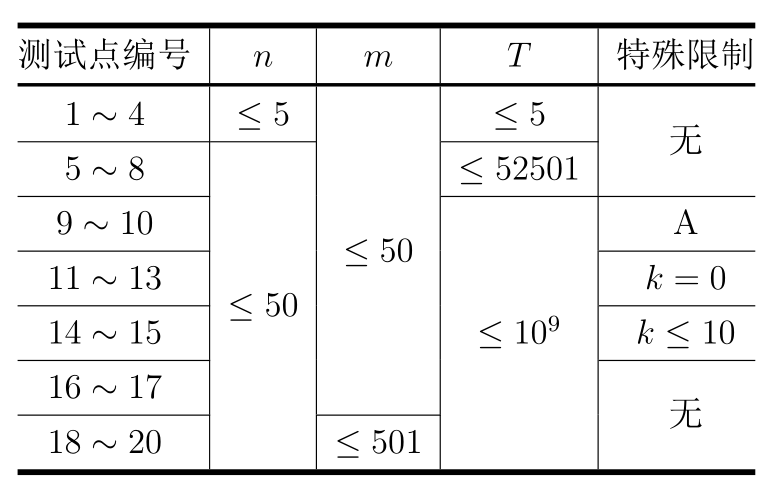
特殊限制 $A:n=m\ 且\ u_i=i,v_i=(i\ mod\ n)+1$。
【来源】
$NOI2020$ $Day1$ $Task1$