| 题目名称 | 3604. [NOI 2021]机器人游戏 |
|---|---|
| 输入输出 | robot.in/out |
| 难度等级 | ★★★★☆ |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 1024 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:0, 通过率:0% | |||
| 关于 机器人游戏 的近10条评论(全部评论) |
|---|
【题目描述】
小R有$m(1\leq m\leq 1000)$个机器人和$m$张纸带,第$i(1\leq i\leq m)$个机器人负责对第$i$张纸带进行操作。对于每张纸带,它们都被从左到右分成了$n(1\leq n\leq 32)$个格子,依次编号为$0, 1,\cdots, n-1$。每个格子有3种状态:格子上写有数字0;格子上写有数字1;格子是一个空格子。
在任意时刻,机器人必须站在纸带上的一个格子中。在设定好机器人在纸带上的初始位置后,第$i$个机器人会依次执行预先设定的操作序列$S_i$,操作由 R、0、1、* 四种字符组成,其中:
1. R 表示机器人向右走一格,如果右边没有格子,则机器人会原地爆炸;
2. 0 表示如果机器人所在格子非空,则将该格子上的数字改为0,否则不修改;
3. 1 表示如果机器人所在格子非空,则将该格子上的数字改为1,否则不修改;
4. * 表示如果机器人所在格子非空,则将格子上的数字$x$改为$1-x$,否则不修改。
第$i$张纸带的状态可以用一个长度为$n$的序列表示,每个元素为 0、1 或 -(空格子),依次表示其每个格子的状态。第$i$张纸带的初始状态称为机器人$i$的输入$X_i$,操作执行完成后纸带的状态称为机器人$i$的输出$Y_i$。注意,如果机器人爆炸了,那么这个机器人就没有输出。
可以发现,如果一个格子为空,那么机器人永远不会修改它。所以每个机器人都有如下特性:如果第$i个机器人所在的纸带上的所有格子都为空,那么它就不会执行任何操作,它的输出即为所有格子都为空。
现在小R给定了每一个机器人的输入$X_i$(即每张纸带的初始状态)以及目标输出$Y_i$。小R希望小D找到一个位置$p(0\leq p<n)$,使得所有机器人都能以其所在纸带的第 $p$个格子为初始位置,在不爆炸的情况下执行完所有操作,并且满足第$i$个机器人的输出为$Y_i$。
小D花了几毫秒解决了问题,现在他想知道,有多少个输入和输出的组合方式使得上述问题有解,即有多少种为每个机器人设定输入$X_0,X_1,\cdots,X_{m-1}$和目标输出$Y_0,Y_1,\cdots,Y_{m-1}$的方式,使得至少存在一个位置$p(0\leq p<n)$,使得所有机器人都能以其所在纸带的第$p$个格子为起点,在不爆炸的情况下执行完所有操作,且满足第$i$个机器人的输出为$Y_i$。请你帮助小D解决这个问题,由于最终的答案可能很大,请你输出答案对$10^9+7$取模后的余数。
两个组合方式不同当且仅当,存在至少一个机器人,它的输入或是目标输出在两个方式中不同。
【输入格式】
第一行包含两个正整数$n,m$,分别表示每张纸带上的格子数和纸带数量。
接下来$m$行,第$i$行输入一个仅包含 R、0、1、* 这四种字符的字符串$S_i$,表示第$i$个机器人的操作序列。
【输出格式】
仅一行一个正整数,表示答案模$10^9+7$后的余数。
【样例1输入】
2 1 1R*
【样例1输出】
9
【样例1解释】

其中 - 表示空格子。
当输入全为空时,初始位置可以是0或1,因为根据题意,输入全为空时机器人不会执行任何操作。
当输入不全为空时,初始位置只能为0,如果初始位置为1机器人一定会爆炸。
所以此时实际执行的操作是将第一格的数字改为1,并将第二格的数字$x$改为$1-x$。
【样例2输入】
3 2 1R0 *
【样例2输出】
1468
【样例2解释】
可以用容斥原理来计算这个样例。
1.初始位置$p=0$可以使得执行完所有操作后满足条件。那么第一个机器人的纸带0号格子要么输入输出都是空,要么目标输出是1(输入无所谓),所以有3种方案;1号格子要么输入输出都是空,要么目标输出是0,也是3种方案;2号格子要么输入输出都是空,要么输入和目标输出相同(因为没有对该格子执行任何操作),同样是3种方案,共 27 种方案。第二个机器人的0号格子要么输入输出都是空,要么输入和目标输出不同,是3种方案,1号和2号格子也都是3种方案,共27种方案。所以总共 27×27=729 种方案。
2.初始位置$p=1$可以使得执行完所有操作后满足条件。那么第一个机器人的纸带三个格子都是3种方案,其中0号格子要么输入输出都为空,要么相同;1号格子要么输入输出都为空,要么目标输出是1;2号格子的输入输出要么都为空,要么输出是0,共27种方案。第二个机器人的1号格子要么输入输出都是空,要么输入和目标输出不同,是3种方案;0号和2号格子要么输入输出都为空,要么输入输出相同,也都是3种方案,共27种方案。总共27×27=729种方案。
3.初始位置$p=2$可以使得执行完所有操作后满足条件。那么第一个机器人的纸带必须输入输出全为空(否则爆炸),只有1种方案。第二个机器人是27种方案,总共27种方案。
4.初始位置$p=0,1$都满足条件。这要求第一个机器人的1号格子输入输出都为空;0号格子的输入输出都为空或都为0;2号格子的输入输出都为空或都为0,所以第一个机器人的纸带有4种方案。第二个机器人0号格子和1号格子都为空,2号格子有3种方案,第二个机器人的0号和1号格子必须都为空,2号格子要么输入输出都为空,要么输入和输出相同,有3种方案。总共12种方案。
5.初始位置$p=0,2$都满足条件。那么第一个机器人的纸带必须输入输出全为空(否则爆炸),只有1种方案。第二个机器人0号和2号格子都为空,1号格子有3种方案。总共3 种方案。
6.初始位置$p=1,2$ 都满足条件。那么第一个机器人的纸带必须输入输出全为空,只有1种方案。第二个机器人1号和2号格子都为空,0号格子有3种方案。总共3种方案。
7.初始位置$p=0,1,2$都满足条件。那么两个机器人的输入输出必须都为空,总共1种方案。
根据容斥原理,最后的答案为729+729+27−12−3−3+1=1468。
【其他输入输出样例】
【数据规模与约定】
对于所有测试点:$1\leq n\leq 32,1\leq m\leq 1000,1\leq |S_i|\leq 100$。
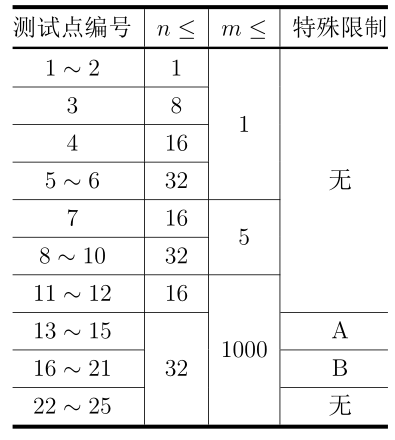
特殊限制 A:操作序列中不存在 R。
特殊限制 B:每个操作序列中,R 的数量至多 15 个。
【来源】
NOI2021 Day2 Task3