| 题目名称 | 1465. 电阻问题 |
|---|---|
| 输入输出 | resistor.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:31, 提交:56, 通过率:55.36% | ||||
|
|
100 | 0.020 s | 0.34 MiB | C++ |
|
|
100 | 0.058 s | 1.31 MiB | C++ |
|
|
100 | 0.060 s | 0.98 MiB | C++ |
|
|
100 | 0.060 s | 1.09 MiB | C++ |
|
|
100 | 0.060 s | 1.09 MiB | C++ |
|
|
100 | 0.060 s | 1.09 MiB | C++ |
|
|
100 | 0.060 s | 1.09 MiB | C++ |
|
|
100 | 0.061 s | 0.98 MiB | C++ |
|
|
100 | 0.061 s | 1.09 MiB | C++ |
|
|
100 | 0.062 s | 1.09 MiB | C++ |
| 本题关联比赛 | |||
| 2022级数学专题练习赛3 | |||
| 2025.6.21 | |||
| 关于 电阻问题 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
哪两个点是a和b?最大那个和最小那个吗?
2017-05-25 13:20
5楼
| ||||
|
果然”学好数理化,走遍天下都不怕“
2016-12-20 16:32
4楼
| ||||
|
最近改程序的能力越来越差了、、、
物理也学得越来越差了、、、、
2014-03-25 19:32
3楼
| ||||
|
今天可浮躁*——*
但谁告诉我为什么标称不能A。。。
2014-03-25 15:57
2楼
| ||||
|
太学霸了……先查了半天物理……
另,推荐拿这题作为(非异或方程的)高斯消元练手,比GPA排名一题强太多,因为本题只要求得出一个精度不高的答案值。 建议看这篇解题报告,比原论文强太多(我就不吐槽论文给标程的找回路了,这才是真·学霸),本文的数据亦由网址中的代码生成,并经我的程序确认 | ||||
【题目描述】
在物理学中,我们常常对一些复杂的电路问题十分头疼,为了便于分析,我们需要把一些电阻的混连电路,用一个等效电阻来取代。而等效电阻的计算往往是十分繁琐的。于是,我们尝试用程序代替我们完成这项任务。程序需要计算的,是一个纯电阻的混连电路中两点间的总电阻。
为了阐述方便,我们建立这样一个模型来描述电路:电路由一个一个结点连接构成,结点就是导线的交点,若两结点间的电路上不存在其它结点,则称这两个结点是两相邻结点。两相邻结点之间只允许有两种情况:
($1$)它们之间是一个已知电阻(如图 $1$):
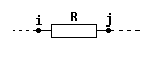
($2$)它们之间是 $x$ 个已知电阻的纯并联电路(如图 $2$):
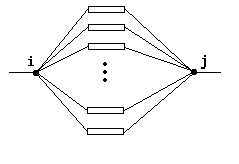
输入保证两相邻结点间总电阻不为零,此模型必然可以描述所有的纯电阻电路。大样例
【输入格式】
第一行是两个整数 $N,M$。表示结点数为 $N$,电路中共有 $M$ 个电阻;
以下 $M$ 行每行有三个整数,$i,j$ 和 $k(1 ≤ i < j ≤ N)$,表示结点 $i$ 和结点 $j$ 之间连结着大小为 $k$ 的电阻(若 $i,j$ 出现多次,则代表这两个节点之间并联多个电阻)。
【输出格式】
仅需输出一个数,就是结点 $1$ 和结点 $N$ 间的总电阻。输出保留二位小数。
【样例1输入】
5 4 1 2 1 2 3 1 3 4 1 4 5 1
【样例1输出】
4.00
【样例2输入】
5 30 5 2 822 2 5 110 5 1 444 2 4 901 4 3 995 1 3 935 3 2 678 5 4 855 4 3 8 4 3 728 1 5 733 3 4 229 1 3 532 1 3 970 2 3 695 2 3 621 1 4 816 5 4 798 1 2 731 5 3 343 1 5 440 1 2 519 5 2 426 3 2 946 4 2 163 3 2 893 2 5 428 2 1 385 3 5 803 4 3 359
【样例2输出】
76.06
【提示】
对于 $30\%$ 的数据,$N \leq 10,M \leq 50$;
对于 $100\%$ 的数据,$N \leq 200,M \leq 50000$;
【来源】
《电脑爱好者》$1999$年第$12$期
杨江明,《论数学策略在信息学问题中的应用》,$IOI2000$国家集训队论文集