| 题目名称 | 2872. [NOIP 2017PJ]棋盘 |
|---|---|
| 输入输出 | chess.in/out |
| 难度等级 | ★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:135, 提交:402, 通过率:33.58% | ||||
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
| 本题关联比赛 | |||
| 近期练习题回顾 | |||
| 关于 棋盘 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
DFS或者Dijkstra,上下左右任意走可以看成环,dp做不到
2025-10-24 23:04
10楼
| ||||
|
啊啊啊啊啊啊啊,我死了!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
| ||||
|
我太水了这种题都不会写
2019-01-04 19:41
8楼
| ||||
|
回复 @10001 :
#include<iostream> using namespace std; int main(){ for(int i=1;i!=0;i++){ cout<<"贾乐佳说:张晏慈是小monkey";} return 0; }
2018-12-24 20:01
7楼
| ||||
|
#include<iostream>
#include<cstring> #include<cstdio> #include<iomanip> #include<algorithm> using namespace std; int minm,m,n,coy,cox,co,a[1050][1050],mina[1050][1050]; i | ||||
|
这种弱题交了那么多次,总算是A了,榜一留念~~~~
2018-10-16 20:06
5楼
| ||||
|
有动态规划的写法吗
2018-10-13 08:38
4楼
| ||||
|
2018-09-22 10:59
3楼
| ||||
|
打了很久的一道水题。。。
暴露蒟蒻本质 | ||||
|
正确率由我来拉低。。。
| ||||
【题目描述】
有一个$m × m$的棋盘,棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。
任何一个时刻,你所站在的位置必须是有颜色的(不能是无色的),你只能向上、下、左、右四个方向前进。当你从一个格子走向另一个格子时,如果两个格子的颜色相同,那你不需要花费金币;如果不同,则你需要花费 $1$ 个金币。
另外,你可以花费 $2$ 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用,而且这个魔法的持续时间很短,也就是说,如果你使用了这个魔法,走到了这个暂时有颜色的格子上,你就不能继续使用魔法;只有当你离开这个位置,走到一个本来就有颜色的格子上的时候,你才能继续使用这个魔法,而当你离开了这个位置(施展魔法使得变为有颜色的格子)时,这个格子恢复为无色。
现在你要从棋盘的最左上角,走到棋盘的最右下角,求花费的最少金币是多少?
【输入格式】
数据的第一行包含两个正整数 $m,n$,以一个空格分开,分别代表棋盘的大小,棋盘上有颜色的格子的数量。
接下来的 $n$ 行,每行三个正整数 $x,y,c$,分别表示坐标为($x,y$)的格子有颜色 $c$。其中 $c=1$ 代表黄色,$c=0$ 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为($1, 1$),右下角的坐标为($m, m$)。
棋盘上其余的格子都是无色。保证棋盘的左上角,也就是($1,1$)一定是有颜色的。
【输出格式】
输出一行,一个整数,表示花费的金币的最小值,如果无法到达,输出$-1$。
【样例输入1】
5 7 1 1 0 1 2 0 2 2 1 3 3 1 3 4 0 4 4 1 5 5 0
【样例输出1】
8
【样例输出1说明】
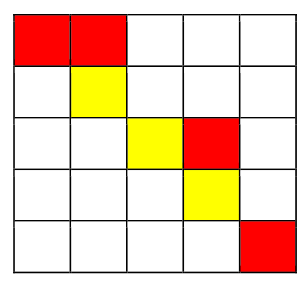
从($1,1$)开始,走到($1,2$)不花费金币;
从($1,2$)向下走到($2,2$)花费 $1$ 枚金币;
从($2,2$)施展魔法,将($2,3$)变为黄色,花费 $2$ 枚金币;
从($2,2$)走到($2,3$)不花费金币;
从($2,3$)走到($3,3$)不花费金币;
从($3,3$)走到($3,4$)花费 $1$ 枚金币;
从($3,4$)走到($4,4$)花费 $1$ 枚金币;
从($4,4$)施展魔法,将($4,5$)变为黄色,花费 $2$ 枚金币;
从($4,4$)走到($4,5$)不花费金币;
从($4,5$)走到($5,5$)花费 1 枚金币;
共花费 8 枚金币。
【样例输入2】
5 5 1 1 0 1 2 0 2 2 1 3 3 1 5 5 0
【样例输出2】
-1
【样例输出2说明】
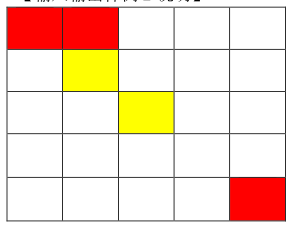
从($1,1$)走到($1,2$),不花费金币;
从($1,2$)走到($2,2$),花费 $1$ 金币;
施展魔法将($2,3$)变为黄色,并从($2,2$)走到($2,3$)花费 $2$ 金币;
从($2,3$)走到($3,3$)不花费金币;
从($3,3$)只能施展魔法到达($3,2$),($2,3$),($3,4$),($4,3$)
而从以上四点均无法到达($5,5$),故无法到达终点,输出$-1$。
【数据规模约定】
对于$30$%的数据,$1 ≤ m ≤ 5, 1 ≤ n ≤ 10$。
对于$60$%的数据,$1 ≤ m ≤ 20, 1 ≤ n ≤ 200$。
对于$100$%的数据,$1 ≤ m ≤ 100, 1 ≤ n ≤ 1,000$。
【来源】
$NOIP2017$普及组第 $3$ 题。