| 题目名称 | 3727. 液体运输 |
|---|---|
| 输入输出 | Xen.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:4, 通过率:25% | ||||
|
|
100 | 1.556 s | 34.57 MiB | C++ |
|
|
40 | 6.072 s | 14.54 MiB | C++ |
|
|
40 | 6.150 s | 51.01 MiB | C++ |
|
|
30 | 6.302 s | 37.56 MiB | C++ |
| 本题关联比赛 | |||
| 4043级NOIP2022欢乐赛2nd | |||
| 关于 液体运输 的近10条评论(全部评论) |
|---|
【题目描述】
$van$ 历经千辛万苦终于找到了那只存在于传说中的 $Zeta$ 晶体,这样他便可以从其中提取出源源不断的 $Xen$ 液体,$van$ 的发家致富之梦终于要实现了!
$van$ 在 $Z$ 市创立了一家工厂,专门为客户公司提供 $Xen$ 液体,而 $Xen$ 液体的运输需要借助 $Z$ 市的下水道网络。
$Z$ 市的下水道网络共有 $n$ 个节点,共 $m$ 条管道将它们全部连接起来,每条管道都有一个最大流量 $a$,表示这条管道最多只能承受 $a$ 流量的液体。$van$ 的工厂和客户公司会各选择其中一个节点打通一条没有流量限制的特殊管道,客户公司的选择是已知的,而若 $van$ 的工厂选择节点 $i$,他将支付 $x_i$ 的代价。
但是,$Xen$ 液体极其粘稠,它自始至终只会形成一股液体,永远不会分流,也就是说,如果 $Xen$ 液体遇到了管道的交叉口,它只会向其中一条流去(但究竟是哪一条是可控的),而如果它超过了当前管道的最大流量,管道就会被撑破,$van$ 也会因此面临牢狱之灾。
现在客户公司发来个 $q$ 个询问,每次给定客户公司选择打通特殊管道的节点和需求的 $Xen$ 液体流量。$van$ 当然不想吃牢饭,于是他问你:
$1.$ 共有多少种打通特殊管道的方案使得 $Xen$ 液体可以在不撑破管道的前提下由 $van$ 的工厂运输到和客户公司。
$2.$ 在上述所有方案中花费代价的最小值是多少。
由于客户公司很急,所以你的算法必须是在线的。
【输入格式】
第一行两个正整数 $n,m$。
接下来 $m$ 行,每行三个正整数 $u,v,a$,表示节点 $u$ 与 $v$ 间有一条最大流量为 $a$ 的管道。
接下来一行 $n$ 个正整数 $x_i$,表示 $van$ 的工厂向节点 $i$ 打通特殊管道的代价。
接下来一行两个正整数 $q,k$,其中 $k∈\{0,1\}$
接下来 $q$ 行,每行三个正整数 $p_0,s_0,mod$,我们令上次询问 $2$ 的答案为 $x$(如果这是第一次询问,则 $x=0$),则令 $p = (p_0 + kx)\% n + 1 , s = (s_0 + kx)\% mod$,表示本次询问客户选择打通特殊管道的节点和要求的 $Xen$ 液体流量。
【输出格式】
$q$ 行,每行两个正整数表示该询问的两个答案。
【样例输入1】
4 5 1 2 2 2 4 3 1 3 3 3 4 2 1 4 2 1 2 3 4 2 1 3 2 114514 1 108 10
【样例输出1】
4 1 1 3
【样例输入输出2】
点击下载样例2
【样例1说明】
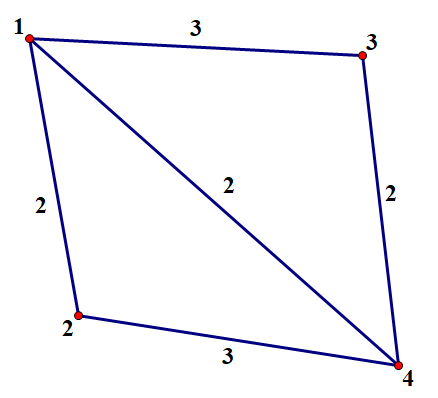
第一次询问 $p = (3 + 1 * 0) \% 4 + 1 = 4, s = (2 + 1 * 0) \% 114514 = 2$,显然节点 $1,2,3,4$ 均可行,最小代价为 $x_1=1$;
第二次询问 $p = (1 + 1 * 1) \% 4 + 1 = 3,s = (108 + 1 * 1) \% 10 = 9$,显然只有节点 $3$ 可行,最小代价为 $x_3=3$.
【数据规模与约定】
对 $20\%$ 的数据,$n≤50,m≤200,q≤100$;
对于另外 $40\%$ 的数据,$k=0$;
对于 $100\%$ 的数据,$n≤2×10^5,m≤4×10^5,q≤4×10^5$;
保证图联通,所有数据均在$int$范围内;
【提示】
输入输出量较大,如果你不会写快读快写:
inline int read(){
int ans=0;
char ch=getchar();
while(!isdigit(ch))ch=getchar();
while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();
return ans;
}
inline void write(int x){
if(x>9)write(x/10);
putchar(x%10+'0');
}
【来源】
$rsr$