| 题目名称 | 1252. Geodetic 集合 |
|---|---|
| 输入输出 | geo.in/out |
| 难度等级 | ★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:60, 提交:115, 通过率:52.17% | ||||
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.003 s | 0.32 MiB | C++ |
|
|
100 | 0.004 s | 0.32 MiB | C++ |
|
|
100 | 0.006 s | 0.30 MiB | C++ |
|
|
100 | 0.006 s | 0.30 MiB | C++ |
|
|
100 | 0.006 s | 0.30 MiB | C++ |
|
|
100 | 0.006 s | 0.32 MiB | C++ |
|
|
100 | 0.006 s | 0.32 MiB | C++ |
|
|
100 | 0.006 s | 0.33 MiB | C++ |
| 本题关联比赛 | |||
| test2 | |||
| 关于 Geodetic 集合 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
真的可以用Floyd诶......求完最短路,对于每个输入,从1到n依次判断每个顶点i是否满足dis[v][i]+dis[i][u]==dis[v][u]即可
| ||||
|
#include<iostream>
#include<cstring> #include<cstdio> using namespace std; int n,m,a[51][51]; int main() { ios::sync_with_stdio(false); freopen("geo.in","r",stdin); freopen("geo.out","w",stdout); cin>>n>>m; for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) a[i][j]=0x3fffffff; a[i][i]=0; } for(int i=1;i<=m;i++) { int l,f; cin>>l>>f; a[l][f]=1; a[f][l]=1; } for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(a[i][k]+a[k][j]<a[i][j]) a[i][j]=a[i][k]+a[k][j]; int k; cin>>k; for(int i=1;i<=k;i++) { int v,u; cin>>v>>u; for(int j=1;j<=n;j++) if(a[v][j]+a[j][u]==a[v][u]) cout<<j<<" "; cout<<endl; } while(1); } | ||||
|
mark
2014-10-05 12:13
4楼
| ||||
|
floyd即可……因为……不判断“是否一定在某一条指定的最短路”,而是“只要在某一条最短路上”就过了……
| ||||
|
题解说是什么 BFS + 递推:
本题考察图的有关知识。算法就是从每个点出发进行BFS扩展,按得到的BFS序列进行递推。然后我用弗洛伊德写出来的时候顿时就泪目了  | ||||
|
崇拝する
2012-11-06 18:02
1楼
| ||||
【题目描述】
图G是一个无向连通图,没有自环,并且两点之间至多只有一条边。我们定义顶点v,u最短路径就是从v到u经过边最少的路径。所有包含在v-u的最短路径上的顶点被称为v-u的Geodetic顶点,这些顶点的集合记作I(v, u)。
我们称集合I(v, u)为一个Geodetic集合。
例如下图中,I(2, 5)={2, 3, 4, 5},I(1, 5)={1, 3, 5},I(2, 4)={2, 4}。
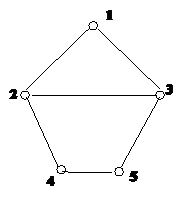
给定一个图G和若干点对v,u,请你分别求出I(v, u)。
【输入格式】
第一行两个整数n,m,分别表示图G的顶点数和边数(顶点编号1-n)
下接m行,每行两个整数a,b表示顶点a和b之间有一条无向边。
第m+2行有一个整数k,表示给定的点对数。
下接k行,每行两个整数v,u。
【输出格式】
共k行,每行对应输入文件中每一个点对v,u,按顶点编号升序输出I(v, u)。同一行的每个数之间用空格分隔。
【样例输入】
5 6 1 2 1 3 2 3 2 4 3 5 4 5 3 2 5 5 1 2 4
【样例输出】
2 3 4 5 1 3 5 2 4
【提示】
100%的数据,n<=40