| 题目名称 | 4116. [统一省选 2025]追忆 |
|---|---|
| 输入输出 | recall.in/out |
| 难度等级 | ★★★★ |
| 时间限制 | 8000 ms (8 s) |
| 内存限制 | 2047 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 查看题解 | 分享题解 |
| 通过:6, 提交:24, 通过率:25% | ||||
|
|
100 | 49.671 s | 756.03 MiB | C++ |
|
|
100 | 56.803 s | 749.22 MiB | C++ |
|
|
100 | 77.293 s | 991.10 MiB | C++ |
|
|
100 | 78.379 s | 753.63 MiB | C++ |
|
|
100 | 80.036 s | 767.62 MiB | C++ |
|
|
100 | 85.419 s | 1121.20 MiB | C++ |
|
|
84 | 138.447 s | 748.91 MiB | C++ |
|
|
48 | 164.548 s | 756.51 MiB | C++ |
|
|
20 | 154.405 s | 437.85 MiB | C++ |
|
|
20 | 163.067 s | 747.29 MiB | C++ |
| 本题关联比赛 | |||
| 国庆欢乐赛2 | |||
| 关于 追忆 的近10条评论(全部评论) |
|---|
【题目背景】
我常常追忆过去。
生命瞬间定格在脑海。我将背后的时间裁剪、折叠、蜷曲,揉捻成天上朵朵白云。
云朵之间亦有分别:积云厚重,而卷云飘渺。生命里震撼的场景掠过我的思绪便一生无法忘怀,而更为普通平常的记忆在时间的冲刷下只留下些许残骸。追忆宛如入梦,太过清楚则无法愉悦自己的幻想,过分模糊却又坠入虚无。只有薄雾间的山水,面纱下的女子,那恰到好处的朦胧,才能满足我对美的苛求。
追忆总在不经意间将我裹进泛黄的纸页里。分别又重聚的朋友,推倒又重建的街道,种种线索协助着我从一个具体的时刻出发沿时间的河逆流而上。曾经的日子无法重来,我只不过是一个过客。但我仍然渴望在每一次追忆之旅中留下闲暇时间,在一个场景前驻足,在岁月的朦胧里瞭望过去的自己,感受尽可能多的甜蜜。美好的时光曾流过我的身体,我便心满意足。
过去已经凝固,我带着回忆向前,只是时常疏于保管,回忆也在改变着各自的形态。这给我的追忆旅程带来些许挑战。
我该在哪里停留?我问我自己。
【题目描述】
给定一个 $n$ 个点 $m$ 条边的有向图 $G$,结点由 $1$ 至 $n$ 编号。第 $i$ ($1 \leq i \leq m$) 条边从 $u_i$ 指向 $v_i$,保证 $u_i < v_i$。节点 $j$ ($1 \leq j \leq n$) 有两个权值 $a_j, b_j$,保证 $[a_1, \ldots, a_n]$ 与 $[b_1, \ldots, b_n]$ 均是 $1 \sim n$ 的排列。 你需要进行 $q$ 次操作。操作有以下三种:
- $1\ x\ y$:交换 $a_x$ 和 $a_y$;
- $2\ x\ y$:交换 $b_x$ 和 $b_y$;
- $3\ x\ l\ r$:你需要输出满足以下两个条件的点 $y$ 中 $b_y$ 的最大值,若不存在满足条件的点则输出 $0$:
1.$l \leq a_y \leq r$。
2.图 $G$ 中存在一条 $x$ 到 $y$ 的有向路径,即存在整数 $k \geq 1$ 与 $k$ 个结点 $p_1, p_2, \ldots, p_k$,
满足$p_1 = x$,$p_k = y$,且对于所有 $1 \leq i < k$,图 $G$ 中存在从 $p_i$ 指向 $p_{i+1}$ 的有向边。
特别地,图 $G$ 中总是存在一条 $x$ 到 $x$ 的有向路径。大樣例
【输入格式】
本题有多组测试数据。
输入的第一行两个整数 $c, T$,分别表示测试点编号和测试数据组数,接下来输入每组测试数据。
样例满足 $c = 0$。 对于每组测试数据,
- 第一行三个整数 $n, m, q$,分别表示图 $G$ 的节点数、图 $G$ 的边数和操作次数,
- 接下来 $m$ 行,第 $i$ ($1 \leq i \leq m$) 行两个整数 $u_i, v_i$,描述一条边,
- 接下来一行 $n$ 个整数 $a_1, a_2, \ldots, a_n$,描述每个节点的 $a$ 权值,
- 接下来一行 $n$ 个整数 $b_1, b_2, \ldots, b_n$,描述每个节点的 $b$ 权值,
- 最后 $q$ 行,第 $i$ ($1 \leq i \leq q$) 行三或四个整数 $o_i, x_i, y_i$ 或 $o_i, x_i, l_i, r_i$,描述一次操作,格式同题目描述。
【输出格式】
对于每个 $3$ 操作输出一行一个整数,表示对应操作的答案。
【样例输入】
0 1 4 4 7 1 2 1 3 2 4 3 4 4 2 3 1 1 3 2 4 3 2 1 3 3 3 2 4 1 1 4 3 1 1 3 2 2 4 3 1 2 3 3 4 1 1
【样例输出】
4 2 3 4 0
【样例说明】
该组样例共有 $1$ 组测试数据。该组测试数据共包含 $7$ 个操作。
- 对于第一个操作,所有满足条件的点为 $2, 4$,因此答案为 $\max\{b_2, b_4\} = 4$。
- 对于第二个操作,所有满足条件的点为 $3$,因此答案为 $b_3 = 2$。
- 对于第三个操作,交换 $a_1, a_4$ 后得到的权值序列 $a$ 为 $[1, 2, 3, 4]$。
- 对于第四个操作,所有满足条件的点为 $1, 2, 3$,因此答案为 $\max\{b_1, b_2, b_3\} = 3$。
- 对于第五个操作,交换 $b_2, b_4$ 后得到的权值序列 $b$ 为 $[1, 4, 2, 3]$。
- 对于第六个操作,所有满足条件的点为 $2, 3$,因此答案为 $\max\{b_2, b_3\} = 4$。
- 对于第七个操作,没有满足条件的点,因此答案为 $0$。
【数据规模与约定】
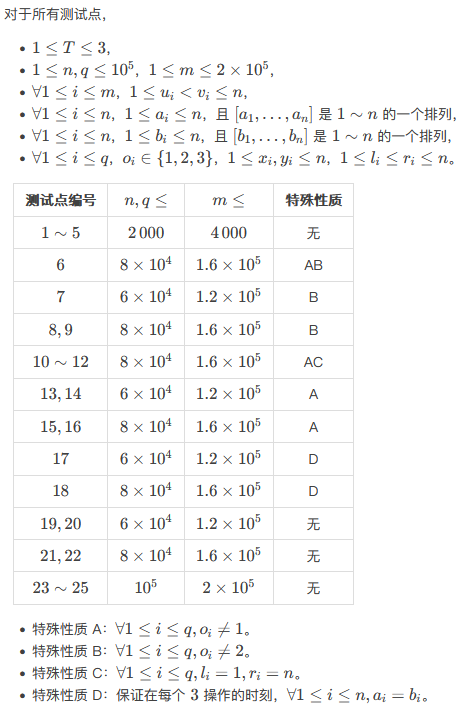
【来源】
2025联合省选day1T2