| 题目名称 | 2403. [NOI 2016]网格 |
|---|---|
| 输入输出 | NOI2016grid.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 1024 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:4, 提交:53, 通过率:7.55% | ||||
|
|
100 | 2.200 s | 194.10 MiB | C++ |
|
|
100 | 5.008 s | 300.69 MiB | C++ |
|
|
100 | 7.516 s | 173.89 MiB | C++ |
|
|
100 | 13.218 s | 74.13 MiB | C++ |
|
|
96 | 4.745 s | 226.97 MiB | C++ |
|
|
96 | 7.695 s | 173.89 MiB | C++ |
|
|
92 | 0.421 s | 196.12 MiB | C++ |
|
|
92 | 5.907 s | 226.97 MiB | C++ |
|
|
92 | 8.059 s | 41.68 MiB | C++ |
|
|
92 | 8.558 s | 43.58 MiB | C++ |
| 关于 网格 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
特判好多。。。捆绑测试稍不注意WA完。。。并且Stack overflow... 需要扩栈
| ||||
|
hash比map强多了,一定要写hash
| ||||
|
回复 @_Itachi :
Orz Itachi神犇
2017-05-25 12:50
2楼
| ||||
|
用map其实也不慢,而且好写的很。
| ||||
【问题描述】
跳蚤国王和蛐蛐国王在玩一个游戏。
他们在一个 n 行 m 列的网格上排兵布阵。其中的 c 个格子中( 0 ≤ c ≤ nm),每个格子有一只蛐蛐,其余的格子中,每个格子有一只跳蚤。
我们称占据的格子有公共边的两只跳蚤是相邻的。
我们称两只跳蚤是连通的,当且仅当这两只跳蚤相邻,或存在另一只跳蚤与这两只跳蚤都连通。
现在,蛐蛐国王希望,将某些( 0 个, 1 个或多个)跳蚤替换成蛐蛐,使得在此之后存在至少两只跳蚤不连通。
例如: 我们用图![]() 表示一只跳蚤,用图
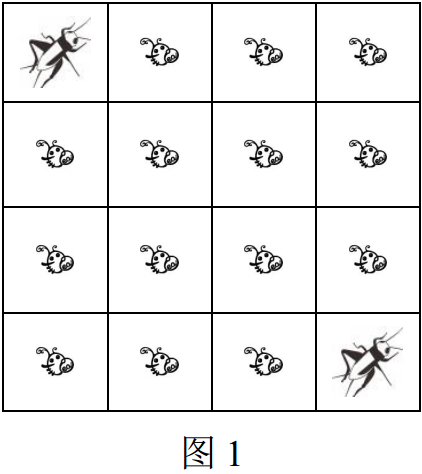
表示一只跳蚤,用图![]() 表示一只蛐蛐,那么图 1 描述了一个 n = 4, m = 4, c = 2 的情况。
表示一只蛐蛐,那么图 1 描述了一个 n = 4, m = 4, c = 2 的情况。
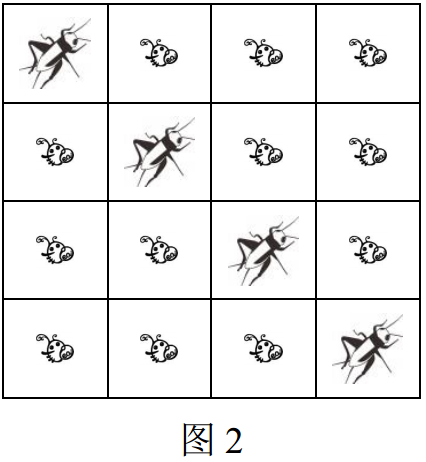
这种情况下蛐蛐国王可以通过将第 2 行第 2 列,和第 3 行第 3 列的两只跳蚤替换为蛐蛐,从而达成他的希望,如图 2 所示。并且,不存在更优的方案,但是可能存在其他替换 2 只跳蚤的方案。
你需要首先判断蛐蛐国王的希望能否被达成。如果能够达成,你还需要最小化被替换的跳蚤的个数。
【输入格式】
每个输入文件包含多组数据。
输入文件的第一行只有一个整数 T,表示数据的组数。 保证 1 ≤ T ≤ 20。
接下来依次输入 T 组数据,每组数据的第一行包含三个整数 n, m, c。 保证 1 ≤ n, m ≤ 10^9, 0 ≤ c ≤ min(nm, 10^5)。
接下来 c 行,每行包含两个整数 x, y,表示第 x 行,第 y 列的格子被一个蛐蛐占据( 1 ≤ x ≤ n, 1 ≤ y ≤ m)。每一组数据当中,同一个蛐蛐不会被多次描述。
同一行相邻的整数之间由一个空格隔开。
【输出格式】
对于每一组数据依次输出一行答案。
如果这组数据中,蛐蛐国王的希望不能被达成,输出 -1。否则,输出被替换的跳蚤的个数的最小值。
【样例输入】
4 4 4 2 1 1 4 4 2 3 1 1 2 2 2 2 1 1 2 2 1 1 0
【样例输出】
2 1 0 -1
【样例说明】
第一组数据就是问题描述中的例子。
对于第二组数据, 可以将第 2 行第 2 列的一只跳蚤替换为蛐蛐,从而使得存在两只跳蚤不连通,并且不存在更优的方案。
对于第三组数据,最初已经存在两只跳蚤不连通,故不需要再进行替换。
对于第四组数据,由于最多只有一只跳蚤,所以无论如何替换都不能存在两只跳蚤不连通。
【更多样例】
【样例 2 输入输出】
见目录下的 NOI2016grid/NOI2016grid2.in 与 NOI2016grid/NOI2016grid2.ans。
【提示】
如果你的程序需要用到较大的栈空间(这通常意味着需要较深层数的递归),请务必仔细阅读选手目录下的文档 stack.pdf,以了解在最终评测时栈空间的限制与在当前工作环境下调整栈空间限制的方法。
PS:来自萌帝的开栈咒语:
#pragma comment(linker, "/STACK:102400000,102400000")
【子任务】
对于全部的测试点,保证 1 ≤ T ≤ 20。 我们记 ∑c为某个测试点中,其 T 组输入数据的所有 c 的总和。
对于所有的测试点, ∑c ≤ 105。 对于全部的数据,满足 1 ≤ n, m ≤ 10^9, 0 ≤ c ≤ nm, 1 ≤ x ≤ n, 1 ≤ y ≤ m。
每个测试点的详细数据范围见下表。表中的 n, m, c 均是对于单个输入数据 (而非测试点)而言的, 也就是说同一个测试点下的 T 组数据均满足限制条件; 而 ∑c 是对于单个测试点而言的。为了方便阅读,“测试点”一列被放到了表格的中间而不是左边。

【来源】
NOI2016 Day1 T2