| 题目名称 | 2562. [NOIP 2016PJ]买铅笔 |
|---|---|
| 输入输出 | pencil.in/out |
| 难度等级 | ☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:372, 提交:696, 通过率:53.45% | ||||
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
| 关于 买铅笔 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
回复 @回归运动 :
666
2024-07-21 09:09
24楼
| ||||
|
#include <bits/stdc++.h>
using namespace std; int main() { freopen("pencil.in","r",stdin); freopen("pencil.out","w",stdout); int n,num[5]={},pri[5]={},alm[5]; cin>>n; for(int i=1;i<=3;i++) {cin>>num[i]>>pri[i]; if(n%num[i]==0) alm[i]=n/num[i]*pri[i]; if(n%num[i]!=0) alm[i]=(n/num[i]+1)*pri[i];} for(int i=1;i<=2;++i) for(int j=1;j<=3-i;++j) if(alm[j]<alm[j+1]) swap(alm[j],alm[j+1]); cout<<alm[3]; }
2024-07-21 09:06
23楼
| ||||
|
so easy
| ||||
|
#include <bits/stdc++.h>
using namespace std; int main() { freopen("pencil.in","r",stdin); freopen("pencil.out","w",stdout); long long n,x,y,d; cin>>n; for(int i=1;i<=3;i++) { cin>>x>>y; if(n%x==0){ if(n/x*y<d){ d=n/x*y; } }else{ if((n/x+1)*y<d){ d=(n/x+1)*y; } } } cout<<d; return 0; } 为啥在评测机上输出0啊? 自己做就没问题 请求大佬给我看看 | ||||
|
我。。。。。。。。
| ||||
|
我有点怂 请问这题是图论吗
2022-04-13 16:17
19楼
| ||||
|
回复 @老霍铁粉 :
jdkslfjsdkl
2020-10-13 20:57
18楼
| ||||
|
。
| ||||
|
.
| ||||
|
我对不起党,对不起国家,排序竟然写错了!!!
| ||||
【题目描述】
P 老师需要去商店买 $n$ 支铅笔作为小朋友们参加 NOIP 的礼物。她发现商店一共有 $3$ 种包装的铅笔,不同包装内的铅笔数量有可能不同,价格也有可能不同。为了公平起 见,P 老师决定只买同一种包装的铅笔。
商店不允许将铅笔的包装拆开,因此 P 老师可能需要购买超过 $n$ 支铅笔才够给小朋友们发礼物。
现在 P 老师想知道,在商店每种包装的数量都足够的情况下,要买够至少 $n$ 支铅笔最少需要花费多少钱。
【输入格式】
第一行包含一个正整数 $n$,表示需要的铅笔数量。
接下来三行,每行用 $2$ 个正整数描述一种包装的铅笔:其中第 $1$ 个整数表示这种包装内铅笔的数量,第 $2$ 个整数表示这种包装的价格。
保证所有的 $7$ 个数都是不超过 $10000$ 的正整数。
【输出格式】
输出到文件中。
输出一行一个整数,表示 P 老师最少需要花费的钱。
【样例输入1】
57 2 2 50 30 30 27
【样例输出1】
54
【提示】
铅笔的三种包装分别是:
- $2$ 支装,价格为 $2$;
- $50$ 支装,价格为 $30$;
- $30$ 支装,价格为 $27$。
P 老师需要购买至少 $57$ 支铅笔。
如果她选择购买第一种包装,那么她需要购买 $29$ 份,共计 $2 \times 29 = 58$ 支,需要花费的钱为 $2 \times 29 = 58$。
实际上,P 老师会选择购买第三种包装,这样需要买 $2$ 份。虽然最后买到的铅笔数量更多了,为 $30 \times 2 = 60$ 支,但花费却减少为 $27 \times 2 = 54$,比第一种少。
对于第二种包装,虽然每支铅笔的价格是最低的,但要够发必须买 $2$ 份,实际的花费达到了 $30 \times 2 = 60$,因此 P 老师也不会选择。
所以最后输出的答案是 $54$。
【样例输入2】
9998 128 233 128 2333 128 666
【样例输出2】
18407
【样例输入3】
9999 101 1111 1 9999 1111 9999
【样例输出3】
89991
【数据规模】
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表:
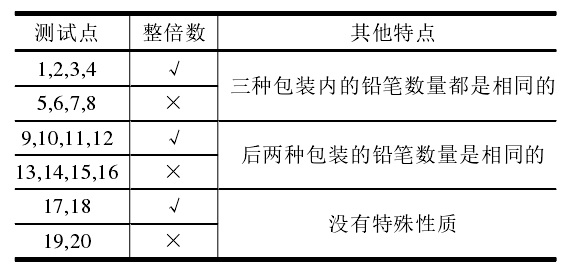
上表中“整倍数”的意义为:若为“√”,表示对应数据所需要的铅笔数量n一定是每种包装铅笔数量的整倍数(这意味着一定可以不用多买铅笔)。
【题目来源】
NOIP2016 普及组题1