| 题目名称 | 3853. [雅礼集训 2018 Day10] 足球大战 |
|---|---|
| 输入输出 | footballwar.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 64 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:1, 通过率:100% | ||||
|
|
100 | 2.578 s | 43.88 MiB | C++ |
| 本题关联比赛 | |||
| 4043级2023省选模拟赛1 | |||
| 关于 足球大战 的近10条评论(全部评论) |
|---|
【题目描述】
有一场足球比赛,还有 $n$ 秒就要结束了,比分还是 $0:0$。
主队每秒进球概率为 $p$,客队每秒进球概率为 $q$,求主队获胜概率。
注意,一秒钟一个队最多进一个球,主队获胜当且仅当主队进球比客队多。
为了避免精度误差,把最后的答案化成最简分数
$\frac{x}{y}$,输出 $x$ 和 $y$ 关于 $(10^9+7)$ 的逆元的乘积即可。
根据费马小定理,
$\frac{x}{y} \bmod (10^9+7) = x\times y^{10^9+5} \bmod (10^9+7)$.
$p$ 和 $q$ 将通过一种特别的方式给出:给出 $pa, pb, qa, qb,$
$p = \frac{pa}{pb}, q = \frac{qa}{qb}$。
【输入格式】
第一行一个正整数 $n$,表示剩余的秒数。
第二行两个整数
$pa, pb, p = \frac{pa}{pb}$,表示主队每秒进球期望数。
第三行两个整数
$qa, qb, q = \frac{qa}{qb}$,表示客队每秒进球期望数。
【输出格式】
输出一行一个整数,表示把答案化成最简分数
$\frac{x}{y}$ 后, $x$ 乘以 $y$ 的逆元关于 $(10^9+7)$ 取模后的值。
【样例1输入】
1 1 2 1 2
【样例1输出】
250000002
【样例1说明】
比赛还剩 $1$ 秒,主队获胜当且仅当主队进球且客队不进球,概率为 $\frac{1}{2} \times (1 - \frac{1}{2}) = \frac{1}{4}$,$4$ 关于 $10^9+7$ 的逆元为 $250\ 000\ 002$。
【样例2输入】
10 1 1 1 3
【样例2输出】
762519270
【样例2说明】
获胜概率为 $1\ -\ \left(\frac{1}{3}\right)^{10}$。
【样例3输入】
233333 233 2333333 566 5666666
【样例3输出】
46387011
【数据规模与约定】
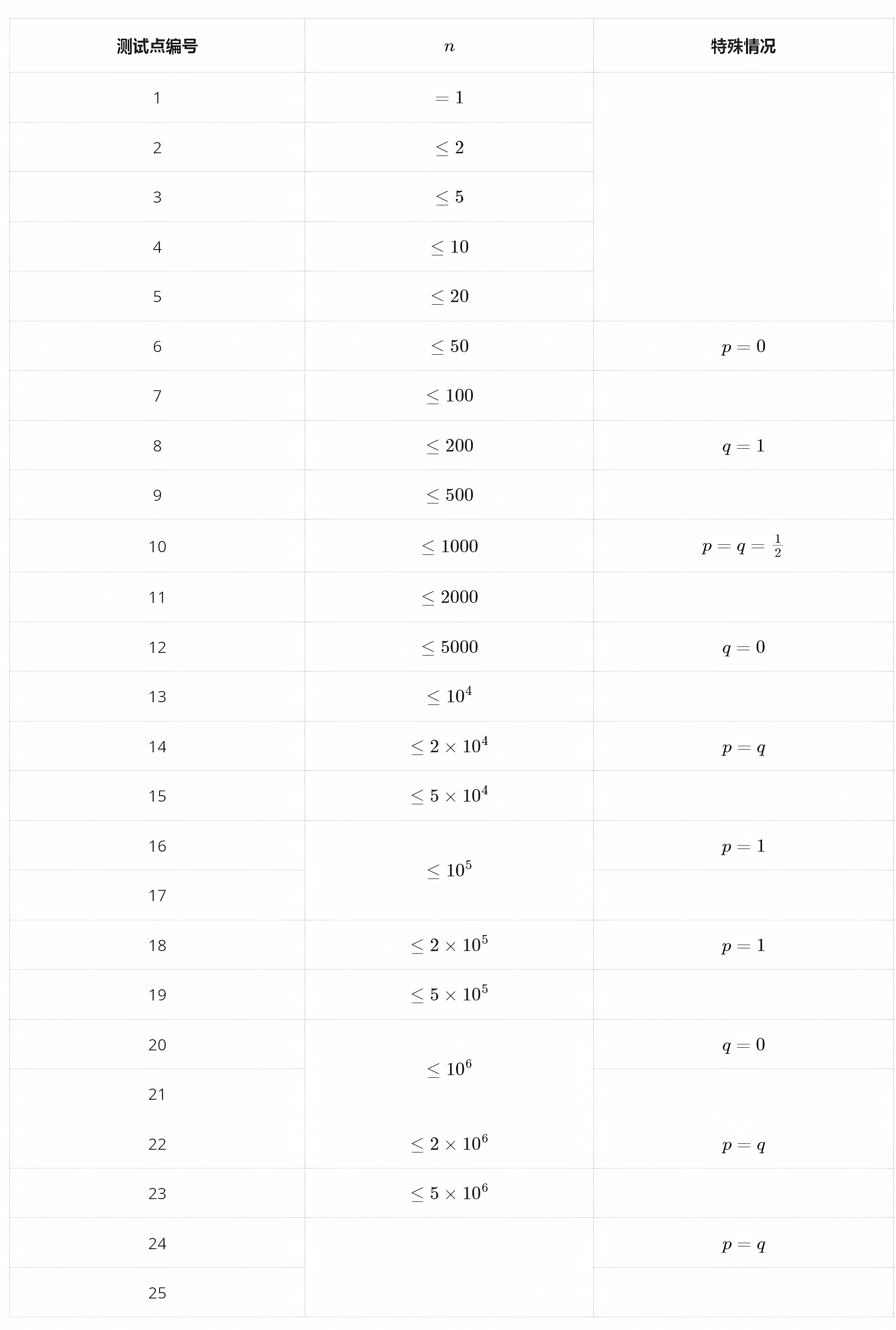
对于所有的数据, $1 \leq n \leq 10^7, 0 \leq pa,qa \leq 10^9, 1 \leq pb, qb \leq 10^9, pa \leq pb, qa \leq qb$。注意常数优化!注意内存限制!
【来源】