| 题目名称 | 2423. [USACO Dec09] 过路费 |
|---|---|
| 输入输出 | toll.in/out |
| 难度等级 | ★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 16 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:126, 提交:246, 通过率:51.22% | ||||
|
|
100 | 0.068 s | 0.33 MiB | C++ |
|
|
100 | 0.069 s | 0.32 MiB | C++ |
|
|
100 | 0.073 s | 0.32 MiB | C++ |
|
|
100 | 0.074 s | 0.32 MiB | C++ |
|
|
100 | 0.075 s | 0.32 MiB | C++ |
|
|
100 | 0.076 s | 0.32 MiB | C++ |
|
|
100 | 0.076 s | 0.32 MiB | C++ |
|
|
100 | 0.076 s | 0.41 MiB | C++ |
|
|
100 | 0.078 s | 0.32 MiB | C++ |
|
|
100 | 0.079 s | 0.32 MiB | C++ |
| 本题关联比赛 | |||
| 近期练习题回顾 | |||
| 关于 过路费 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
有重边!!!!!
| ||||
|
dfg法国红酒发鬼地方读后感多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多多灌灌灌灌灌过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过灌灌灌灌灌过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过灌灌灌灌灌过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过江湖救急军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军军汉库克扩扩扩扩扩扩扩扩扩扩扩扩扩扩过过过过过过过过过过过或军军军军军军军军军军军军军军过过过过过过过过过错错错错错错错错错错错错好纠结军军军军军军军军军绿若或付图多付付与过过过过若多晕付付付付付付付付付付付付付付付付付付付付付付付付付付付付付付付付付付有人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人烦人若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若若frrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrfffffffffffffffffffffffffffrff
2018-08-29 15:39
1楼
| ||||
【题目描述】
跟所有人一样,农夫约翰以着宁教我负天下牛,休教天下牛负我(原文:宁我负人,休教人负我)的伟大精神,日日夜夜苦思生财之道。为了发财,他设置了一系列的规章制度,使得任何一只奶牛在农场中的道路行走,都要向农夫约翰上交过路费。
农场中由$N(1 <= N <= 250)$片草地(标号为$1$到$N$),并且有$M(1 <= M <= 10000)$条双向道路连接草地$A_j$和$B_j(1 <= A_j <= N; 1 <= B_j <= N)$。奶牛们从任意一片草地出发可以抵达任意一片的草地。FJ已经在连接$A_j$和$B_j$的双向道路上设置一个过路费$L_j(1 <= L_j <= 100,000)$。
可能有多条道路连接相同的两片草地,但是不存在一条道路连接一片草地和这片草地本身。最值得庆幸的是,奶牛从任意一片草地出发,经过一系列的路径,总是可以抵达其它的任意一片草地。
除了贪得无厌,FJ都不知道该说什么好。FJ竟然在每片草地上面也设置了一个过路费$C_i(1 <= C_i <= 100000)$。从一片草地到另外一片草地的费用,是经过的所有道路的过路费之和,加上经过的所有的草地(包括起点和终点)的过路费的最大值。
任劳任怨的牛们希望去调查一下她们应该选择那一条路径。她们要你写一个程序,接受$K(1 <= K <= 10,000)$个问题并且输出每个询问对应的最小花费。第i个问题包含两个数字$s_i和t_i(1 <= s_i <= N; 1 <= t_i <= N; s_i != t_i)$,表示起点和终点的草地。
考虑下面这个包含5片草地的样例图像:
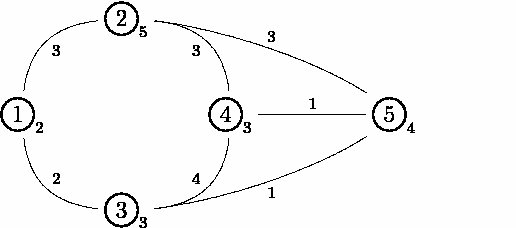
从草地$1$到草地$2$的道路的“边过路费”为$3$,草地$2$的“点过路费”为$5$。
要从草地$1$走到草地$4$,可以从草地$1$走到草地$3$再走到草地$5$最后抵达草地$4$。如果这么走的话,需要的“边过路费”为$2+1+1=4$,需要的点过路费为$4$(草地$5$的点过路费最大),所以总的花费为$4+4=8$。
而从草地$2$到草地$3$的最佳路径是从草地$2$出发,抵达草地$5$,最后到达草地$3$。这么走的话,边过路费为$3+1=4$,点过路费为$5$,总花费为$4+5=9$。
【输入格式】
* 第$1$行: 三个空格隔开的整数: $N, M,K$
* 第$2$到第$N+1$行: 第$i+1$行包含一个单独的整数: $C_i$
* 第$N+2$到第$N+M+1$行: 第$j+N+1$行包含$3$个由空格隔开的整数: $A_j, B_j,L_j$
* 第$N+M+2$倒第$N+M+K+1$行: 第$i+N+M+1$行表示第$i$个问题,包含两个由空格隔开的整数$s_i$和$t_i$
【输出格式】
* 第$1$到第$K$行: 第$i$行包含一个单独的整数,表示从$s_i$到$t_i$的最小花费。
【样例输入】
5 7 2 2 5 3 3 4 1 2 3 1 3 2 2 5 3 5 3 1 5 4 1 2 4 3 3 4 4 1 4 2 3
【样例输出】
8 9
【来源】
$USACO Dec 09$