| 题目名称 | 3432. [NOI Online 2020 2nd PJ]荆轲刺秦王 |
|---|---|
| 输入输出 | noi_online_bandit.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:5, 提交:47, 通过率:10.64% | ||||
|
|
100 | 2.351 s | 13.96 MiB | C++ |
|
|
100 | 2.916 s | 0.00 MiB | C++ |
|
|
100 | 4.979 s | 18.84 MiB | C++ |
|
|
100 | 6.483 s | 0.00 MiB | C++ |
|
|
100 | 8.369 s | 31.58 MiB | C++ |
|
|
85 | 3.952 s | 53.93 MiB | C++ |
|
|
80 | 3.842 s | 18.84 MiB | C++ |
|
|
70 | 23.107 s | 158.06 MiB | C++ |
|
|
70 | 23.146 s | 158.06 MiB | C++ |
|
|
55 | 4.620 s | 151.77 MiB | C++ |
| 关于 荆轲刺秦王 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
半星怎么突然成三星半了……
 (隐身次数不特判居然能得80分!) (隐身次数不特判居然能得80分!)
2020-09-20 19:20
2楼
| ||||
|
回复 @夜莺 :
逗你玩呢
2020-09-19 09:28
1楼
| ||||
3432. [NOI Online 2020 2nd PJ]荆轲刺秦王
★★★☆ 输入文件:noi_online_bandit.in
输出文件:noi_online_bandit.out
简单对比时间限制:3 s 内存限制:512 MiB
【题目描述】
时隔数年,刺客荆轲再次来到咸阳宫,试图刺杀嬴政。
咸阳宫的地图可以描述为一个 $n$ 行 $m$ 列的矩形。在这里,我们规定每一行中从左到右为 $x$ 轴正方向,每一列中从下到上为 $y$ 轴正方向,左下角的点坐标为 $(1,1)$。矩形中的点可以分为 $4$ 种:
1. 起点,也就是荆轲的所在点,在地图中用字符 S 代表。
2. 终点,也就是嬴政的所在点,在地图中用字符 T 代表。
3. 卫兵,在地图中用一个正整数 $a_{i,j}$ 代表。在这里,一个卫兵 $(i,j)$ 可以观察到与他曼哈顿距离小于 $a_{i,j}$ 的点。也就是卫兵 $(i,j)$ 可以观察到所有满足 $|x-i|+|y-j|<a_{i,j}$ 的点 $(x,y)$。
4. 空地,在地图中用字符 . 代表。
荆轲的正常移动方式为每秒向八连通的任意方向前进一格。如下图,中间的点为荆轲当前所在点,每一秒,他可以走向其余的八个点。
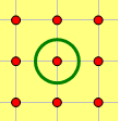
需要注意的是,正常移动时,荆轲不能踏进任何一个有卫兵或者卫兵能观察到的格子。当然,他也不能走出咸阳宫,也就是说,无论何时,荆轲的坐标 $(x,y)$ 都必须满足 $1\le x\le m$ 且 $1\le y\le n$。 荆轲还有两种技能:隐身和瞬移。
1. 隐身:下一秒荆轲进入隐身状态,卫兵观察不到荆轲,荆轲可以进入卫兵的观察范围内,但仍然不能进入卫兵所在的格子。注意这个状态只能维持一秒。
2. 瞬移:荆轲下一秒移动的距离改为 $d$,但这时只能向上下左右四个方向移动。即可以移动到 $(x+d,y)$,$(x-d,y)$,$(x,y+d)$,$(x,y-d)$。
在本题中,两种技能可以同时使用,而且不考虑冷却时间,即一次用完可以立即用下一次,两种技能都分别有使用次数限制,你也可以不用完所有次数。
现在给出咸阳城的地图,请计算荆轲到达秦王所在点所需的最短时间。此外,在所用时间相同情况下,荆轲希望使用的两种技能总次数尽可能少;在所用时间与技能次数相同情况下,荆轲希望使用的隐身次数尽可能少。
【输入格式】
第一行五个整数 $n$, $m$, $c_1$, $c_2$, $d$,代表地图的大小为 $n\times m$,隐身的使用限制次数为 $c_1$,瞬移的使用限制次数为 $c_2$ 和一次瞬移的距离为 $d$。
接下来 $n$ 行,每行 $m$ 个元素。每个元素为字符 S、T、. 或者一个正整数 $a_{i,j}$,代表一个格点,具体含义详见题目描述。
【输出格式】
若荆轲无法到达秦王所在点,则输出一行一个 $-1$。
否则输出一行三个整数 $t$, $u_1$, $u_2$,依次代表所需的最短时间,隐身的使用次数与瞬移的使用次数。
【样例输入1】
5 4 0 0 5 . 1 T 1 . . . 2 . 1 . . S . . . 1 . . .
【样例输出1】
3 0 0
【样例 1 解释】
起点为 $(1,2)$,荆轲可以依次走到 $(1,3)$, $(2,4)$, $(3,5)$ 到达终点。
【样例输入2】
8 6 2 3 3 . S . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 . 2 . 2 . . . 1 . T . 3 . 1 . . 3
【样例输出2】
3 1 3
【样例 2 解释】
起点为 $(2,8)$,荆轲可以依次走到 $(2,5)$, $(5,5)$, $(5,2)$,需要注意的是,即使最后一步到达终点,但因为终点在卫兵的观察范围之内,所以仍然需要隐身进入。
【样例输入3】
8 6 5 5 2 . S . . . . . . . . . . . . . . . . 1 1 3 2 . 1 2 3 2 2 1 3 3 2 4 1 4 3 2 6 1 5 T 2 8 1 6 3 2 10
【样例输出3】
-1
【数据规模与约定】
对于测试点 $1\sim 6$:$n$, $m\le 10$,$c_1=c_2=0$,保证所需的最短时间不超过 $5$ 或者无解。
对于测试点 $7\sim 10$:$n$, $m\le 20$,$c_1=c_2=0$,保证 T 的位置不在任何一个卫兵的观察范围之中。
对于测试点 $11\sim 12$:$n$, $m\le 20$,$c_1=0$
对于测试点 $13\sim 14$:$n$, $m\le 20$,$c_1$, $c_2 \le 5$。
对于测试点 $15\sim 16$:卫兵个数不超过 $350$。
对于所有测试点:$2\le n$, $m\le 350$,$1\le a_{i,j}\le 350$,$0\le c_1$, $c_2\le 15$,$1\le d\le 350$。
保证 S 的位置不在任何卫兵的观察范围中。
【来源】
NOI Online2020 入门组 第二轮 Task 2
数据来源:Acwing & 洛谷