| 题目名称 | 3602. [NOI 2021]量子通信 |
|---|---|
| 输入输出 | qi.in/out |
| 难度等级 | ★★★★ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 384 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:3, 通过率:0% | ||||
|
|
80 | 25.307 s | 91.01 MiB | C++ |
|
|
0 | 74.976 s | 27.11 MiB | C++ |
|
|
0 | 74.979 s | 27.15 MiB | C++ |
| 关于 量子通信 的近10条评论(全部评论) |
|---|
【题目描述】
小 Z 正在自学量子计算机相关知识,最近他在研究量子通信章节,并遇到了一个有趣的问题。在该问题中,Alice 和 Bob 正在进行量子通信,它们的通信语言是一个大小为$n$的字典$S$,在该字典中,每一个单词$s_i(1\leq i\leq n)$都可以用一个256位的01串来表示。在本题中$s_i$可以通过调用函数gen来生成,选手可以在题目目录下的gen.cpp中查看,该函数的参数n、a1、a2将由输入数据给出。
Alice 和 Bob 接下来要进行$m$次通信,每次通信由 Alice 向 Bob 传输恰好一个字典中的单词。然而,两人使用的通信信道并不可靠,会受到噪音的干扰。更具体地,对于第$i$次传输,记 Alice 传输的原单词为$x_i$,该 0101 串会受噪音干扰而翻转最多$k_i$位。换句话说,记 Bob 这次收到的01串为$yi$,它与$xi$相比,可能有最多$ki$位是不同的,并且$yi$可能不在字典$S$中出现。
与此同时,Bob 得知坏人 Eve 也潜入了两人的通信信道,并准备干扰两人的通信。
他的干扰方式是将 Bob 收到的01串变为任意的256位01串,并且这个串可能不在字典$S$中出现。Eve 非常狡猾,他不一定会对每次通信都进行干扰。
现在 Bob 找来了你帮忙,对于接下来的每次通信,你需要根据 Bob 最终收到的01串以及这次通信的噪音干扰阈值$k_i(0\leq k_i\leq 15)$,判断这次通信是否有可能没有受到 Eve 的干扰(即 Bob 收到的01串可以由字典中的某个单词翻转至多$k_i$位后得到)。本次通信如果有可能没受到 Eve 干扰,请你输出1,否则输出0。Bob 很信任你的能力,所以你需要在线地回答结果,具体要求见输入格式。
为了降低读入用时,Bob 收到的串将用长度为64的16进制串给出,16进制串中包含数字字符0$\sim$9与大写英文字母A$\sim$F,其中字符A$\sim$F依次表示数值10$\sim$15。
16进制串可以逐位转化为01串,例如:5 对应 0101,A 对应 1010,C 对应 1100。
【输入格式】
输入数据第一行包含四个正整数$n,m,a_1,a_2$,分别表示字典大小,通信次数,以及gen函数中参数a1和a2的初始值。
选手需要在自己的程序中调用题目描述中提到的gen函数生成单词表,选手可以复制并使用gen.cpp中的代码,程序中的布尔数组s[N+1][256]即为所有的单词。
接下来$m$行,每行包含一个长度为64的16进制串和一个非负整数$k_i$,分别表示第$i$次通信 Bob 最终收到的 01串和噪音干扰阈值。
为了强制选手在线地回答询问,选手根据16进制串还原出256位01串后,将01串每一位异或上$lastans$才能得到这次通信中 Bob 收到的真实01 串,其中$lastans\in\{0,1\}$表示上一次询问的答案,第一个询问前$lastans$初始值为0。
注意:使用 scanf 和 printf 函数读入或输出 unsigned long long 类型变量时,对应的占位符为 llu。
【输出格式】
输出共$m$行,每行一个整数0或1表示当前询问的答案。
【询问举例】
为了方便解释题意,我们使用了直接给出字典中单词、缩小单词长度为 4、允许离线地回答询问等方式,对简化的情况举例。
考虑字典大小为$n=2$,单词有1010和0111。
对于询问B=1011和$k_1=1$,回答应该是 1,通过翻转1010的第4位(从高位到低位,下同)得到。
对于询问1=0001和$k_2=2$,回答应该是 1,通过翻转0111的第2、3位得到。
对于询问1=0001和$k_3=1$,回答应该是 0。
• 翻转1010至多1位可得 1010、0010、1110、1000、1011。
• 翻转0111至多1位可得 0111、1111、0011、0101、0110。
• 无法得到 1=0001,它必定是由 Eve 干扰得到的。
【输入输出样例】
【数据规模与约定】
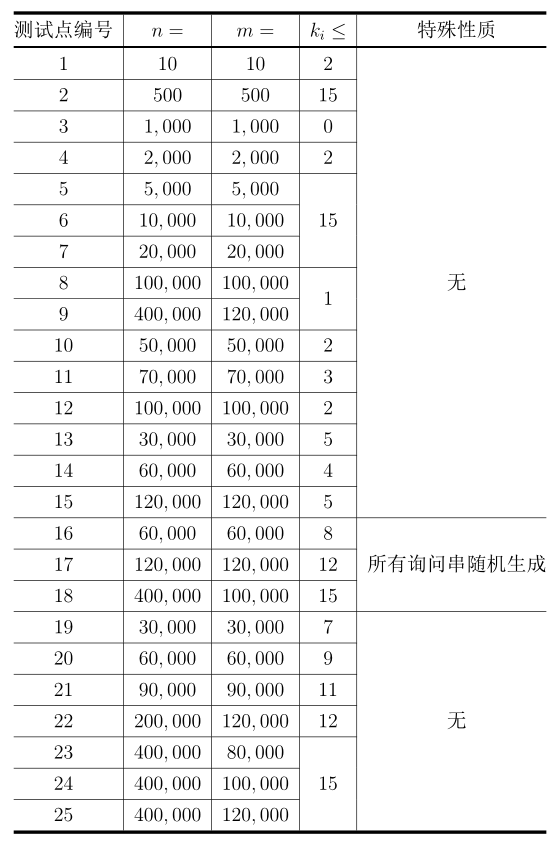
对于所有测试点:$1\leq n\leq 4\times 10^5,1\leq m\leq 1.2\times 10^5,0\leq k\leq 15$,$a_1$和$a_2$在$[0,2^{64}-1]$之间均匀随机生成。
【来源】
NOI2021 Day2 Task1