| 题目名称 | 4117. [统一省选 2025]图排列 |
|---|---|
| 输入输出 | graperm.in/out |
| 难度等级 | ★★★★☆ |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:2, 通过率:0% | ||||
|
|
88 | 5.869 s | 32.04 MiB | C++ |
|
|
0 | 4.504 s | 26.14 MiB | C++ |
| 关于 图排列 的近10条评论(全部评论) |
|---|
【题目描述】
小 Q 有 $m$ 个互不相同的正整数二元组 $\{(a_i, b_i)\}_{i=1}^m$,其中对于所有 $1 \leq i \leq m$,$1 \leq a_i < b_i \leq n$。这 $m$ 个二元组满足如下性质:不存在 $1 \leq i, j \leq n$ 满足 $a_i < a_j < b_i < b_j$。
小 D 有一个 $1 \sim n$ 的排列 $p$。小 Q 和小 D 利用他们手上的二元组和排列一起构建了一张 $n$ 个点 $m$ 条边的无向图 $G = (V, E)$,其中 $V = \{1, 2, \ldots, n\}$,$E = \{(p_{a_i}, p_{b_i}) \mid i \in \{1, 2, \ldots, m\}\}$。
现在小 I 得知了图 $G$,他想要知道在小 Q 的 $m$ 个二元组所具有的性质的前提下,小 D 手中的排列 $p$ 可能是什么。由于小 I 手中的信息不足,排列 $p$ 有很多种可能,小 I 希望你可以告诉他其中字典序最小的那一个。
小 Q,小 D 和小 I 是很好的朋友,他们保证不会欺骗彼此,因此存在至少一个排列 $p$ 满足条件。
【输入格式】
本题有多组测试数据。输入的第一行两个整数 $c, T$,分别表示测试点编号和测试数据组数,接下来输入每组测试数据。样例满足 $c = 0$。
对于每组测试数据,第一行两个整数 $n, m$,分别表示图 G 的点数和边数,接下来 $m$ 行,第 $i (1 \leq i \leq m)$ 行两个整数 $u_i, v_i$,描述图 $G$ 的一条边。
【输出格式】
对于每组测试数据,输出一行一个 $1 \sim n$ 的排列 $p$,表示题设条件下字典序最小的排列。数据保证存在至少一个排列 $p$ 满足条件。
【样例输入】
0 2 4 2 1 3 4 2 4 5 2 3 4 2 3 1 1 4 3 4
【样例输出】
1 2 4 3 1 3 2 4
【样例说明】
该组样例共有 $2$ 组测试数据。
- 对于第一组测试数据,
- 如果小 D 的排列为 $[1, 2, 3, 4]$,那么小 Q 拥有的二元组为 $\{(1, 3), (2, 4)\}$,但取 $i = 1, j = 2$ 有 $1 < 2 < 3 < 4$,因此不满足小 Q 的二元组的性质。
- 如果小 D 的排列为 $[1, 2, 4, 3]$,那么小 Q 拥有的二元组为 $\{(1, 4), (2, 3)\}$,可以证明其满足性质。
- 对于第二组测试数据,如果小 D 的排列为 $[1, 3, 2, 4]$,那么小 Q 拥有的二元组为 $\{(2, 3), (3, 4), (1, 2), (1, 4), (2, 4)\}$,可以证明其满足性质。
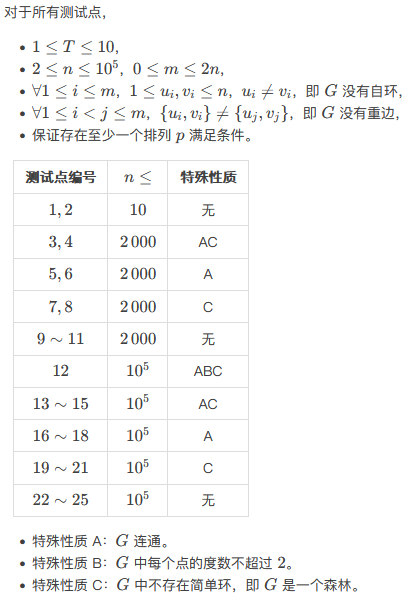
【数据规模与约定】
【来源】
2025联合省选day1T3