| 题目名称 | 2559. [NOIP 2016]组合数问题 |
|---|---|
| 输入输出 | problem.in/out |
| 难度等级 | ★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 查看题解 | 分享题解 |
| 通过:237, 提交:1010, 通过率:23.47% | ||||
|
|
100 | 0.064 s | 6.81 MiB | C++ |
|
|
100 | 0.067 s | 6.24 MiB | C++ |
|
|
100 | 0.130 s | 31.00 MiB | C++ |
|
|
100 | 0.133 s | 34.12 MiB | C++ |
|
|
100 | 0.149 s | 31.12 MiB | C++ |
|
|
100 | 0.152 s | 29.65 MiB | C++ |
|
|
100 | 0.152 s | 31.12 MiB | C++ |
|
|
100 | 0.152 s | 31.21 MiB | C++ |
|
|
100 | 0.154 s | 31.21 MiB | C++ |
|
|
100 | 0.190 s | 17.30 MiB | C++ |
| 本题关联比赛 | |||
| 2017noip | |||
| 暑假综合模拟2 | |||
| SBOI摆烂比赛① | |||
| 2022级数学专题练习赛7 | |||
| 关于 组合数问题 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
说句闲话:http://172.30.1.3/cogs/submit/code.php?id=7SzeaWqgk 5 9 4 7 行 代 码 但没事了我们写出整正解了
| ||||
|
2025-10-16 19:40
14楼
| ||||
|
为什么我自己程序在自己电脑上一个都过不去(返回非0值 ),传进来过了18个。
2018-10-30 17:01
13楼
| ||||
|
回复 @小字、小瓶子 :
m大于n的时候 组合数等于0
2018-10-29 16:50
12楼
| ||||
|
前缀和,数学优化,边界特判就过了,然而算法一点也不优美
| ||||
|
m竟然能大于n???
| ||||
|
尴尬,为了方便调试预处理先到了6(样例范围),然后交上去忘记改了……
2017-09-12 09:13
9楼
| ||||
|
| ||||
|
因为小细节错了两遍之后终于过了
| ||||
|
YY出了递推公式,前缀和优化查询...
| ||||
【题目描述】
组合数 $C_n^m$ 表示的是从 $n$ 个物品中选出 $m$ 个物品的方案数。举个例子,从 $(1,2,3)$ 三个物品中选择两个物品可以有 $(1,2),(1,3),(2,3)$ 这三种选择方法。根据组合数的定义,我们可以给出计算组合数 $C_n^m$ 的一般公式:
$C_n^m=\frac{n!}{m!(n-m)!}$
其中 $n!=1\times2\times\cdots\times n$;特别地,定义 $0 != 1$。
小葱想知道如果给定 $n,m$ 和 $k$,对于所有的 $0\leq i\leq n,0\leq j\leq \min(i,m)$ 有多少对 $(i,j)$ 满足 $C_i^j$ 是 $k$ 的倍数。
【输入格式】
第一行有两个整数 $t, k$,其中 $t$ 代表该测试点总共有多少组测试数据,$k$ 的意义见【问题描述】。
接下来 $t$ 行每行两个整数 $n,m$,其中 $n,m$ 的意义见【问题描述】。
【输出格式】
$t$ 行,每行一个整数代表所有的 $0\leq i\leq n,0\leq j\leq \min(i,m)$ 中有多少对 $(i, j)$ 满足 $C_i^j$ 是 $k$ 的倍数。
【样例1输入】
1 2 3 3
【样例1输出】
1
【提示】
在所有可能的情况中,只有$C_2^1$是 $2$ 的倍数。
【样例2输入】
2 5 4 5 6 7
【样例2输出】
0 7
【数据范围】
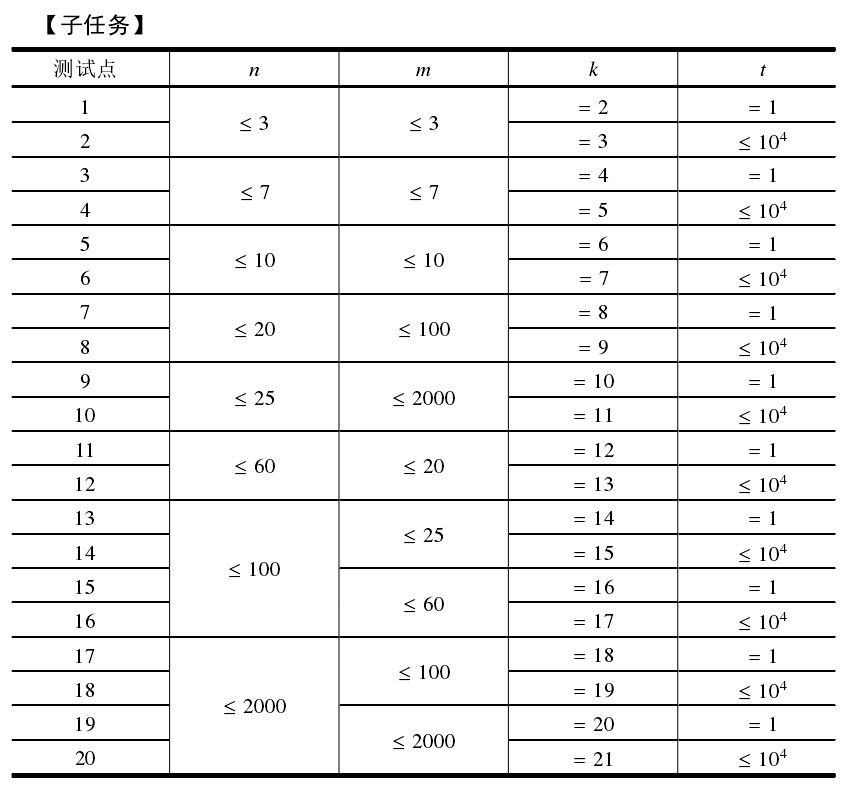
【来源】
$NOIP2016\ Day2\ Task1$
