| 题目名称 | 1308. [HNOI 2006]潘多拉的宝盒 |
|---|---|
| 输入输出 | pandora.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:3, 提交:9, 通过率:33.33% | ||||
|
|
100 | 0.030 s | 0.42 MiB | C++ |
|
|
100 | 0.095 s | 13.74 MiB | C++ |
|
|
100 | 1.169 s | 1.12 MiB | C++ |
|
|
10 | 0.004 s | 0.47 MiB | C++ |
|
|
0 | 0.001 s | 0.29 MiB | C++ |
|
|
0 | 0.002 s | 0.34 MiB | C++ |
|
|
0 | 0.015 s | 0.41 MiB | C++ |
|
|
0 | 10.000 s | 0.47 MiB | C++ |
|
|
0 | 10.000 s | 1.12 MiB | C++ |
| 关于 潘多拉的宝盒 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
……
| ||||
|
没有SPJ几乎不能做
| ||||
|
没有SPJ几乎不能做
| ||||
【题目描述】
传说中,有个神奇的潘多拉宝盒。如果谁能打开,便可以拥有幸福、财富、爱情。可是直到真的打开,才发现与之相随的还有灾难、不幸。
其实,在潘多拉制造这个宝盒的时候,设置了一些咒语来封锁住灾难与不幸。然而,直到科技高度发达的今天,人们才有希望弄懂这些咒语。所以说,上千年来,人们只得忍受着各种各样的疾病和死亡的痛苦。
然而,人类的命运从此改变了。经过数十年的研究,NOI组织在最近终于弄清楚了潘多拉咒语的原理。
咒语是由一个叫做咒语机的机器产生的。用现在的名词来解释,咒语机其实就是一个二进制产生器,它产生的一个二进制字符串(这个字符串叫做咒语源)经加密后就形成了咒语。二进制产生器的结构是这样的: 它由n个元件组成,不妨设这n个元件的标号为0到n-1。在每个时刻,都有且仅有一个信号,它停留在某个元件上。一个信号就是一个二进制字符串。最开始,有一个空串信号停留在元件0上。在某个时刻,如果有一个信号s停留在元件I上,那么,这时元件i可以将信号后面加一个0,然后把信号传给元件pi,0,也可以将信号后面加一个1,然后传给元件pi,1。也就是说,下一个时刻有可能,一种可能是一个信号S0(表示字串S后面加一个0形成的字串)仪在元件pi,0上,另一种可能是有一个信号S1停留在元件pi,1上。
有的元件可以将停留在它上面的信号输出,而输出的信号就成为了咒语源,这样的元件叫做咒语源输出元。
不难发现,有些口语源是可能由一个咒语机产生的,而另一些咒语源则不行。
例如,下图的咒语机能产生1,11,111,1111,„„等咒语源,但是不能产生0,10,101等咒语源。
在这个盒子上,有K个咒语机,不妨将这些咒语机从0到K-1标号。可能有这种情况,一个咒语机i能够产生的口语源,咒语机j都能产生。这时,我们称咒语机j是咒语机i的升级。而衡量这个例子的复杂程度的一种办法是:看这个盒子上升级次数最多的一个咒语机。即:找到一个最长的升级序列a1,a2„„at。该升级序列满足:序列中任意两个咒语机的标号都不同,且都是0到k-1(包含0和k-1)之间的整数,且咒语机a2是咒语机a1的升级,咒语机a3是咒语机a2的升级,„„,咒语机at是咒语机at-1的升级。 你想远离灾难与不幸吗?你想从今以后沐浴幸福的阳光吗?请打开你的潘多拉之盒吧。不过在拱形它之前,你先得计算一下宝盒上最长的升级序列。
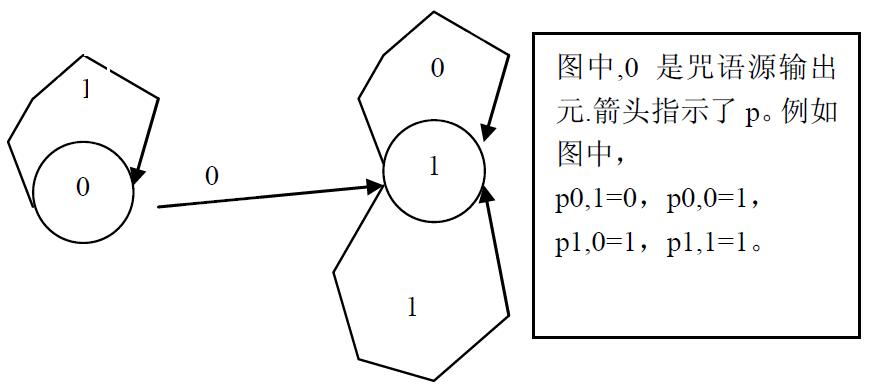
【输入格式】
从文件中读入数据,文件第一行是一个正整数S,表示宝盒上咒语机的个数,(1≤S≤50)。
文件以下分为S块,每一块描述一个咒语机,按照咒语机0,咒语机1„„咒语机S-1的顺序描述。每一块的格式如下。
一块的第一行有两个正整数n,m。分别表示该咒语机中元件的个数、咒语源输出元的个数(1≤m≤n≤50)。 接下来一行有m个数,表示m个咒语源输出元的标号(都在0到n-1之间)。
接下来有n行,每一行两个数。第i行(0≤i≤n-1)的两个数表示pi,0和pi,1(当然,都在0到n-1之间)。
【输出格式】
输出文件的第一行有一个正整数t,表示最长升级序列的长度。 第二行有t个数,用于描述该序列。有可能最长的升级序列不止一个,这时输出任意一个都可以。
【样例输入1】
4
1 1
0
0 0
2 1
0
1 1
0 0
3 1
0
1 1
2 2
0 0
4 1
0
1 1
2 2
3 3
0 0
【样例输出1】
3 3 1 0
【样例输入2】
3
1 1
0
0 0
3 1
0
0 1
2 0
1 2
9 1
0
0 1
2 3
4 5
6 7
【样例输出2】
3
2 1 0