| 题目名称 | 3069. [eJOI 2020]喷泉 |
|---|---|
| 输入输出 | fountain.in/out |
| 难度等级 | ★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:2, 通过率:50% | ||||
|
|
100 | 2.086 s | 24.70 MiB | C++ |
|
|
30 | 7.719 s | 4.16 MiB | C++ |
| 关于 喷泉 的近10条评论(全部评论) |
|---|
【题目描述】
大家都知道喷泉吧?现在有一个喷泉由 $n$ 个圆盘组成,从上到下以此编号为 $1 \sim n$,第 $i$ 个圆盘的直径为 $d_i$,容量为 $c_i$,当一个圆盘里的水大于了这个圆盘的容量,那么水就会溢出往下流,直到流入半径大于这个圆盘的圆盘里。如果下面没有满足要求的圆盘,水就会流到喷泉下的水池里。
现在给定 $q$ 组询问,每一组询问这么描述: 向第 $r_i$ 个圆盘里倒入 $v_i$ 的水,求水最后会流到哪一个圆盘停止。
如果最终流入了水池里,那么输出 $0$。
注意,每个询问互不影响。
【输入格式】
第一行两个整数 $n,q$ 代表圆盘数和询问数。
接下来 $n$ 行每行两个整数 $d_i,c_i$ 代表一个圆盘。
接下来 $q$ 行每行两个整数 $r_i,v_i$ 代表一个询问。
【输出格式】
$q$ 行每行一个整数代表询问的答案。
【样例输入】
6 5 4 10 6 8 3 5 4 14 10 9 4 20 1 25 6 30 5 8 3 13 2 8
【样例输出】
5 0 5 4 2
【样例说明】
前两个询问的解释如下图所示:
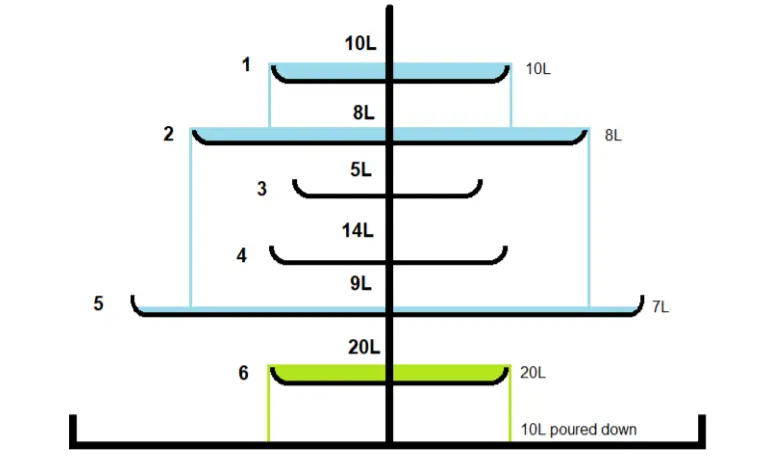
【数据规模与约定】
对于$30\%$的数据,$n \leq 1000,q \leq 2000$。
对于另外$30%$的数据,$d_i$为严格单调递增序列。
对于$100\%$的数据,$2 \leq n \leq 10^5,1 \leq q \leq 2 \times 10^5,1 \leq C_i \leq 1000,1 \leq D_i,V_i \leq 10^9,1\leq r_i \leq n$。