| 题目名称 | 3584. [统一省选 2021]支配 |
|---|---|
| 输入输出 | dominator.in/out |
| 难度等级 | ★★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:22, 通过率:4.55% | ||||
|
|
100 | 4.233 s | 0.00 MiB | C++ |
|
|
30 | 0.113 s | 0.00 MiB | C++ |
|
|
30 | 1.878 s | 0.00 MiB | C++ |
|
|
30 | 2.545 s | 0.00 MiB | C++ |
|
|
30 | 11.372 s | 10.85 MiB | C++ |
|
|
30 | 14.049 s | 0.00 MiB | C++ |
|
|
30 | 14.242 s | 10.87 MiB | C++ |
|
|
20 | 5.952 s | 20.60 MiB | C++ |
|
|
20 | 6.175 s | 0.00 MiB | C++ |
|
|
10 | 6.442 s | 0.00 MiB | C++ |
| 关于 支配 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
好耶

2021-12-04 16:13
1楼
| ||||
【题目描述】
给定一张 $n$ 个点 $ m$ 条边的有向图 $G$,其顶点从 $1\sim n$ 编号。
对于任意两个点 $u,v$,若从顶点 $1$ 出发到达顶点 $v$ 的所有路径都需要经过顶点 $u$,则称顶点 $u$ 支配顶点 $v$。特别地,每个顶点支配其自身。
对于任意一个点 $v$,我们将图中支配顶点 $v$ 的顶点集合称为 $v$ 的受支配集 $D_v$ 。
现在有 $q$ 次互相独立的询问,每次询问给出一条有向边,请你回答在图 $G$ 中加入该条边后,有多少个顶点的受支配集发生了变化。
【输入格式】
第一行三个整数 $n,m,q$,分别表示图中的顶点数、边数,以及询问数。
接下来 $m$ 行每行两个整数 $x_i ,y_i$ ,表示一条有向边 $x_i\rightarrow y_i$ 。
接下来 $q$ 行每行两个整数 $s_i ,t_i$ ,表示每次询问加入的边 $s_i\rightarrow t_i$ 。
数据保证给出的图 $G$ 中,从 $1$ 号点出发能到达所有其他点,并且图中不包含重边与自环。
【输出格式】
对于每个询问输出一行一个整数表示答案。
【样例1输入】
6 6 3 1 2 1 3 3 4 4 5 2 6 4 1 5 6 3 2 2 4
【样例1输出】
1 0 2
【样例1说明】
对于原图,六个点的受支配集分别为:$D_1 = \{1\},D_2 = \{1,2\},D_3 = \{1,3\},D_4 =\{1,3,4\},D_5 = \{1,3,4,5\},D_6 = \{1,2,6\}$。
加入 $5 → 6$ 后,$D_6 = \{1,6\}$,其他点受支配集不变。
加入 $3 → 2$ 后没有点受支配集改变。
加入 $2 → 4$ 后 $D_4 = \{1,4\},D_5 = \{1,4,5\}$,其他点受支配集不变。
【样例2/3】
【数据规模与约定】
对于所有测试数据:$1\leq n\leq 3000,1\leq m\leq 2\times n, 1\leq q\leq 2\times 10^4$。
每个测试点的具体限制见下表:
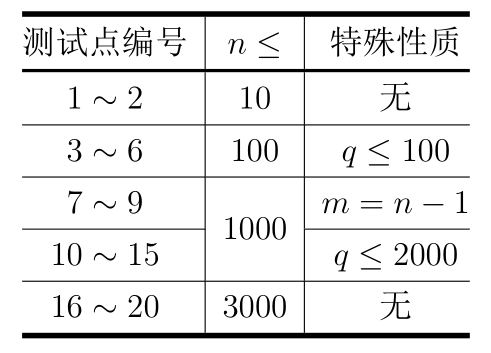
【来源】
2021统一省选A卷 Day2 Task3