| 题目名称 | 4130. 一道简单题 |
|---|---|
| 输入输出 | yaep.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 1500 ms (1.5 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:26, 通过率:3.85% | ||||
|
|
100 | 12.209 s | 18.99 MiB | C++ |
|
|
88 | 11.235 s | 19.26 MiB | C++ |
|
|
88 | 13.354 s | 19.15 MiB | C++ |
|
|
64 | 19.645 s | 103.77 MiB | C++ |
|
|
64 | 19.664 s | 103.78 MiB | C++ |
|
|
64 | 19.709 s | 103.77 MiB | C++ |
|
|
64 | 19.792 s | 103.74 MiB | C++ |
|
|
20 | 7.450 s | 4.86 MiB | C++ |
|
|
12 | 27.730 s | 9.88 MiB | C++ |
|
|
12 | 27.785 s | 9.87 MiB | C++ |
| 关于 一道简单题 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
六百六十六
2025-04-07 20:45
1楼
| ||||
【题目背景】
Alice 和 Bob 又要进行新一轮的博弈了。
【题目描述】
Alice 给出了一个具有 $n$ 个点和 $m=n-1$ 条边的无向连通图。
Bob 觉得这个图太丑陋了,他决定删掉这个图的一些边。
具体地,有 $q$ 次操作,第 $i$ 次 Bob 只会删掉编号不是$i$ 的倍数的边。操作之间独立,即每次操作开始前图都是一开始的图。
对于每次操作,图会变为若干个连通块,Alice 要对于每个连通块,选择一个初始点,然后对于每个初始点,遍历一遍这个初始点所在的连通块。同时钦定一个顺序访问初始点。
我们对遍历的定义如下:如果一个节点 $u$ 存在一个相邻的节点 $v$(如果有多个 $v$ 满足条件,则 Alice 会找到最优的 $v$),且 $v$ 没有被访问过,则去访问 $v$,同时认为走过了边 $(u,v)$;否则回到上一个访问的节点。重复这一操作直到该连通块没有点没有被访问过。
现在每条边上有一个编号,我们将按照经过边的顺序从前到后写出边上的编号,记最后写出的序列为 $s$。Alice 需要最小化 $s$ 的字典序。
我们定义长度为 $n$ 的序列 $a$ 的字典序比长度为 $m$ 的序列 $b$ 的字典序小,当且仅当满足下面两个条件的任意一个:
·$\exists i\le n,a_i<b_i$ 且 $\forall j<i,a_j=b_j$。
·$\forall i\le n,a_i=b_i$ 且 $n<m$。
我们认为:每组数据中第 $i$ 条输入的边的编号为 $i$。
【输入格式】
第一行,测试点编号 $C$ 和数据组数 $T$。
对于每组数据,输入格式如下:
第一行三个正整数 $n,m,q$,表示图的节点数,边数和询问数。
接下来 $m$ 行,每行两个正整数 $u,v$,代表一条边的两个端点。
【输出格式】
对于每组数据,输出格式如下:
共 $q$ 行,每行输出一个不用空格分隔的序列代表字典序最小的 $s$。
注意:如果序列为空,输出 -1。
【样例1输入】
0 2 5 4 3 1 2 2 3 3 4 4 5 7 6 4 1 2 1 3 2 4 2 5 3 6 3 7
【样例1输出】
1234 24 3 125634 264 36 4
【样例1说明】
样例 1 的第二组数据如图所示:
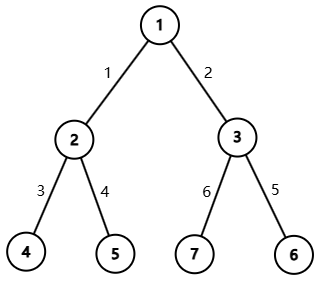
【样例2/3/4/5】
【样例 2 解释】
该样例包含 3 组数据,分别满足测试点 1,6,9 的限制。
【样例 3 解释】
该样例包含 2 组数据,分别满足测试点 12,13 的限制。
【样例 4 解释】
该样例包含 3 组数据,分别满足测试点 14,16,19 的限制。
【样例 5 解释】
该样例包含 1 组数据,满足测试点 23 的限制。
【数据规模与约定】
注意:所有样例均满足 $C=0$。
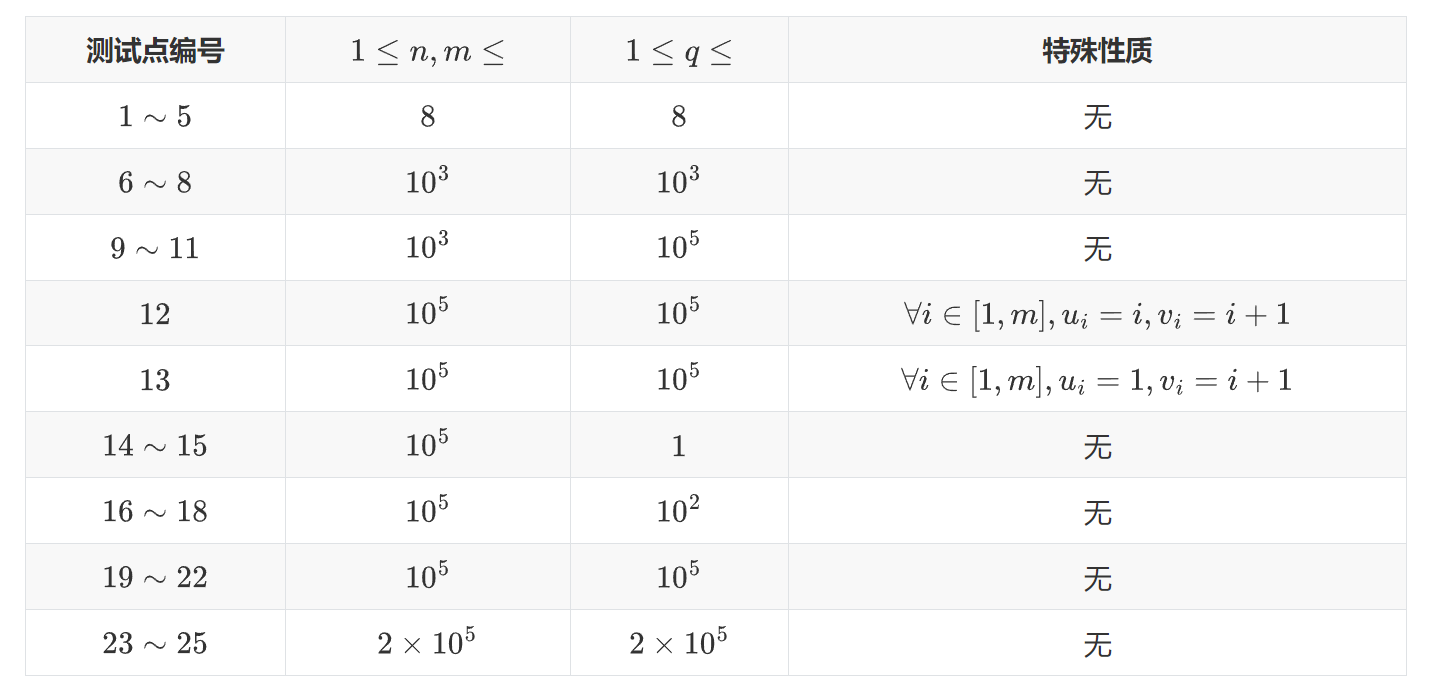
对于 $100\%$ 的数据,$1\le T\le 3,1\le n,m,q\le 2\times 10^5$。
【来源】
校际联合邀请赛第5场-入门组T4