| 题目名称 | 2453. 次小生成树 |
|---|---|
| 输入输出 | secmst.in/out |
| 难度等级 | ★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
 哒哒哒哒哒！
于2016-09-04加入 |
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过：110， 提交：228， 通过率：48.25% | ||||
 op_组撒头屯 |
100 | 0.192 s | 18.80 MiB | C++ |
 AAAAAAAAAA |
100 | 0.228 s | 34.75 MiB | C++ |
 YPZ_979 |
100 | 0.261 s | 26.25 MiB | C++ |
 test |
100 | 0.281 s | 26.25 MiB | C++ |
 skylee |
100 | 0.287 s | 22.81 MiB | C++ |
|
yrtiop |
100 | 0.288 s | 29.58 MiB | C++ |
|
skylee |
100 | 0.291 s | 22.81 MiB | C++ |
 hee |
100 | 0.304 s | 38.65 MiB | C++ |
|
skylee |
100 | 0.305 s | 22.81 MiB | C++ |
|
hee |
100 | 0.305 s | 38.65 MiB | C++ |
| 本题关联比赛 | |||
| 防止浮躁的小练习v0.9 | |||
| 2025暑期集训第8场 | |||
| 关于 次小生成树 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
100+行代码，又*又长
AAAAAAAAAA
2017-10-29 12:02
14楼
| ||||
|
很久之前写的，发现算法竟然是O(n)的，现在竟然看不懂了???
| ||||
|
树剖对倍增的优越性
| ||||
|
回复 @NVIDIA :
论乱立flag的危害（PS：之前似乎有位大牛立flag说联赛不考概率期望树链剖分，结果23333）  Albert S. Chang
2017-02-20 20:51
11楼
| ||||
|
写起来感觉好麻烦，联赛应该不考吧......
 NVIDIA
2016-11-07 16:20
10楼
| ||||
|
样例不过能90分，数据水的可以= =
| ||||
|
| ||||
|
呃呃呃。。。bzoj上死活不过结果INF有开小了。。
请记住const long long INF=~(1ll<<63); 充满血与泪的教训啊！  _Itachi
2016-09-04 20:30
7楼
| ||||
|
| ||||
|
BZOJ终于过了，居然忘开long long了
 Hzoi_chairman
2016-09-04 20:12
5楼
| ||||
CSU_Turkey
AntiLeaf
svideo【题目描述】
小 $C$ 最近学了很多最小生成树的算法，$Prim$ 算法、$Kurskal$ 算法、消圈算法等等。 正当小 $C$ 洋洋得意之时，小 $P$ 又来泼小 $C$ 冷水了。小 $P$ 说，让小 $C$ 求出一个无向图的次小生成树，而且这个次小生成树还得是严格次小的，也就是说： 如果最小生成树选择的边集是 $E_M$，严格次小生成树选择的边集是 $E_S$，那么需要满足：($value(e)$ 表示边 $e$ 的权值)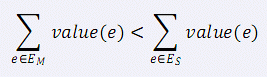
这下小 $C$ 蒙了，他找到了你，希望你帮他解决这个问题。大样例
【输入格式】
第一行包含两个整数$N$和$M$，表示无向图的点数与边数。 接下来$M$行，每行$3$个数$x$ $y$ $z$ 表示，点 $x$ 和点 $y$ 之间有一条边，边的权值为 $z$。
【输出格式】
包含一行，仅一个数，表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)
【样例输入】
5 6
1 2 1
1 3 2
2 4 3
3 5 4
3 4 3
4 5 6
【样例输出】
11
【提示】
数据中无向图无自环；
$50$% 的数据$N≤2000 , M≤3000$；
$80$% 的数据$N≤5,0000 , M≤10,0000$；
$100$% 的数据$N≤10,0000 , M≤30,0000$ ，边权值非负且不超过 $10^9$。
【来源】
$BZOJ$ $1977$