| 题目名称 | 2898. [WC 2018] 通道 |
|---|---|
| 输入输出 | tunnel.in/out |
| 难度等级 | ★★★★ |
| 时间限制 | 4000 ms (4 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:2, 提交:4, 通过率:50% | ||||
|
|
100 | 62.280 s | 16.22 MiB | C++ |
|
|
100 | 88.824 s | 6.03 MiB | C++ |
|
|
40 | 10.907 s | 74.32 MiB | C++ |
|
|
20 | 2.622 s | 68.38 MiB | C++ |
| 关于 通道 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
| ||||
【题目描述】
11328 年,C 国的科学家们研发了一种高速传送通道,可以在很短的时间内把居民
从通道的一端送往另一端,这些通道都是双. 向. 的。
美中不足的是,这种传送通道需要进行大量的维护和检修。经过规划,C 国总统决
定在M 城中新建这种通道,在M 城中,建立了$n$ 个传送站和$3 \times (n - 1)$ 条传送通道,
这些传送通道被分为$3$ 组,每一组都包含了$(n - 1)$ 条通道。
当任意一组通道运行时,居民都可以通过这组通道从任意一个传送站前往任意的
另一个传送站。也就是说,所有的传送站都会被通道所连通。
三组通道按照1、2、3 的顺序轮流运行,循环反复。在任意一个时刻,都有且只有
一组传送通道可以使用。形式化地,在第i 天中,有且只有第$((i - 1) mod 3 + 1)$ 组通
道运行。
C 国著名科学家Access Globe 正在进行一项社会调查实验:调查两个传送站之间
的传送通道使用者的信息。Access Globe 的计划是这样的:
• 选定两个传送站a、b
• 第一天,他从a 出发,使用正在运行的这组通道沿最短路径到达b,并调查经过
的所有通道上使用者的信息
• 第二天,他从b 出发,使用正在运行的这组通道沿最短路径到达a,并调查经过
的所有通道上使用者的信息
• 第三天,他从a 出发,使用正在运行的这组通道沿最短路径到达b,并调查经过
的所有通道上使用者的信息
Access Globe 知道每一条传输线路在运行时的使用者人数。他希望找出一对a、b,
使得在整个实验过程中所有经过的通道的使用者数量之和最大。Access Globe 希望参
加CCF NOI 2018 冬令营的你帮他解决这个简单的小问题。如果你成功地解决了这个
问题,Access Globe 会送你一份小礼物——100 分!
【输入格式】
从文件tunnel.in 中读入数据。
输入文件的第$1$ 行包含一个正整数$n$,表示传送站的个数,传送站从1 到n 编号;
输入文件的第$2$ 到第$n$ 行,每行包含$3$ 个数$u; v;w$,表示第一组通道中有一条连
接$u; v$ 的通道,其运行时使用者数量为$w$ 人;
输入文件的第$(n + 1)$ 到第$(2n - 1)$ 行,每行包含3 个数$u; v;w$,表示第二组通道
中有一条连接$u; v$ 的通道,其运行时使用者数量为$w$ 人;
输入文件的第$2n$ 到第$(3n - 2)$ 行,每行包含$3$ 个数$u; v;w$,表示第三组通道中有
一条连接$u; v$ 的通道,其运行时使用者数量为$w$ 人。
【输出格式】
输出到文件tunnel.out 中。
输出文件共1 行,包含一个整数,表示最大的使用者数量之和。
【样例1 输入】
5
1 2 2
1 3 0
1 4 1
4 5 7
1 2 0
2 3 1
2 4 1
2 5 3
1 5 2
2 3 8
3 4 5
4 5 1
【样例1 输出】
27
【样例1】
见选手目录下的tunnel/tunnel1.in 与tunnel/tunnel1.ans。
【样例1 解释】
下图为样例中M 城的传送站和传输线路情况。其中点和虚线交替的线条、虚线条
和实线条分别表示第一组、第二组和第三组通道。
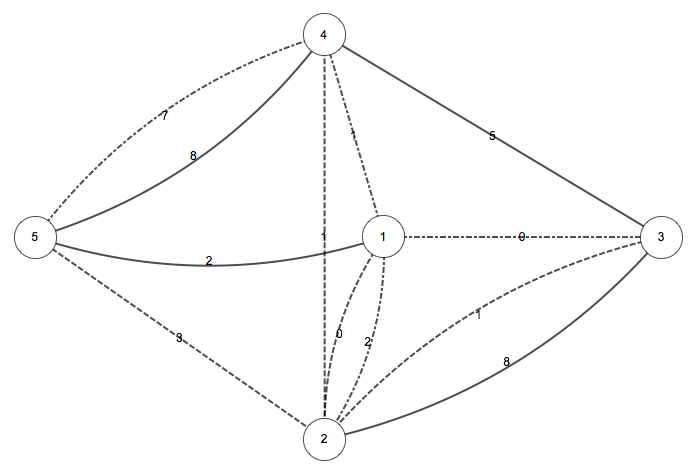
一种可行的方案是选择$a = 2; b = 5$,这样的使用者数量之和为$(3) + (8 + 5 + 1) + (2 + 1 + 7) = 27$。
【样例2】
见选手目录下的tunnel/tunnel2.in 与tunnel/tunnel2.ans。
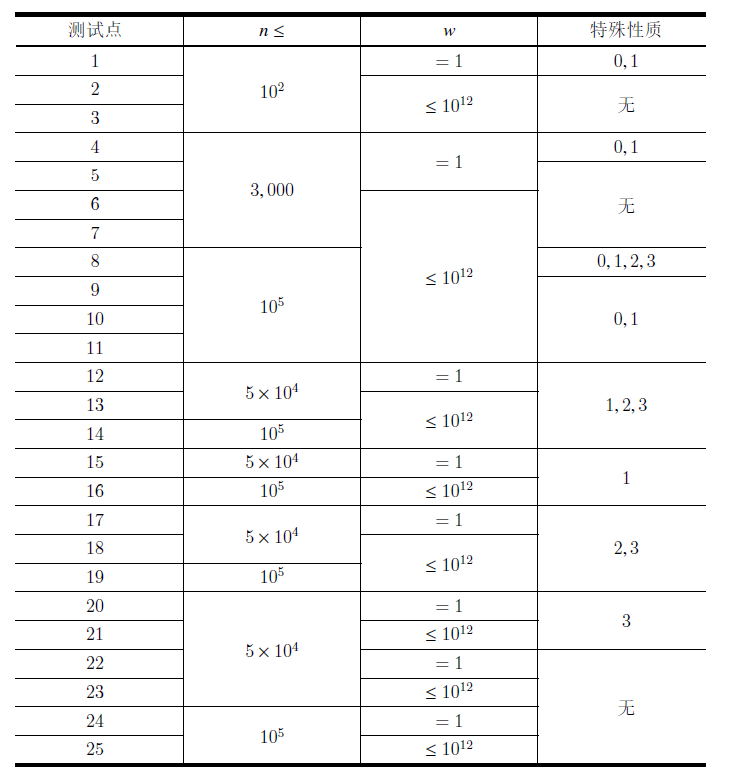
【子任务】
对于所有数据,$2 \leq n \leq 10^5$; $0 \leq w \leq 10^{12}$。
特殊性质0:任意两组通道构成完全相同。
特殊性质1:第二组通道和第三组通道构成完全相同。
特殊性质2:对于第二组的每一个传送站,最多只有两个通道可以到达它,且编号
为 x; y 的传送站之间通过一. 条. 通道直接连接充要条件是 $|x-y| = 1$。
特殊性质3:对于第三组的每一个传送站,最多只有两个通道可以到达它。
【提示】
• 在两组通道中,可能都包含了连接传送站x; y 的通道,此时我们认为这两条通道
是不. 同. 的。
• 特殊性质中,A 组通道和B 组通道的‘‘构成完全相同’’ 是指:如果在A 组中$u; v$
之间存在一条使用人数为w 的通道,那么在B 组中$u; v$ 之间一定也存在一条使
用人数为 w 的通道。是否相同与. 描. 述. 方. 式. 与. 描. 述. 顺. 序. 均. 无. 关. 。即在构成完全相
同的两组通道 A 和 B 中,通. 道. 输. 入. 的. 顺. 序. 不. 一. 定. 相. 同. ,每. 条. 通. 道. 的. 端. 点. 的. 输. 入.
顺. 序. 也. 不. 一. 定. 相. 同. (对于 A、B 组中一条连接 $u; v$ 的使用人数为$ w $的通道,一
种可能出现的输入为:A 组通道中输入u v w,而B 组通道中输入v u w)。