| 题目名称 | 4119. [统一省选2025]岁月 |
|---|---|
| 输入输出 | years.in/out |
| 难度等级 | ★★★★ |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:0, 通过率:0% | |||
| 关于 岁月 的近10条评论(全部评论) |
|---|
【题目背景】
希望大家一直记得我。
“希望大家永远忘了我。”
【题目描述】
小 Y 有一个 $n$ 个节点、$m$ 条边的带权无向图 $G$,节点由 1 至 $n$ 编号。第 $i$ ($1 \leq i \leq m$) 条边连接 $u_i$ 和 $v_i$,边权为 $w_i$。保证 $G$ 连通且没有重边自环。
小 Y 预见到岁月将会磨灭图 $G$ 的痕迹,而这会导致一些边变成有向边,另一些边直接消失。具体地,图 $G$ 历经岁月将会磨损为 $n$ 个节点的带权有向图 $G'$,其中对于第 $i$ ($1 \leq i \leq m$) 条边,$G'$ 上
- 有 $\frac{1}{4}$ 的概率同时存在 $u_i$ 向 $v_i$ 和 $v_i$ 向 $u_i$ 的有向边,它们的边权均为 $w_i$;
- 有 $\frac{1}{4}$ 的概率存在 $v_i$ 向 $u_i$、边权为 $w_i$ 的有向边,而不存在其反向边;
- 有 $\frac{1}{4}$ 的概率存在 $u_i$ 向 $v_i$、边权为 $w_i$ 的有向边,而不存在其反向边;
- 有 $\frac{1}{4}$ 的概率 $u_i$ 和 $v_i$ 之间没有边。
所有 $m$ 个随机事件是独立的。
小 Y 认为一个无向图的核心是最小生成树,而一个有向图的核心是最小外向生成树。称图 $G'$ 的一个边子集 $E$ 是外向生成树,当且仅当 $|E| = n - 1$ 且存在一个节点 $x$ 可以只经过 $E$ 中的有向边到达图 $G'$ 上的所有节点。图 $G'$ 的最小外向生成树即为图 $G'$ 上边权和最小的外向生成树。
小 Y 希望图的核心历经岁月侵蚀也保持不变,于是他想知道,有多大的概率,图 $G'$ 的最小外向生成树存在,且其边权和等于图 $G$ 的最小生成树边权和。
你需要将答案对 $(10^9 + 7)$ 取模。可以证明答案一定为有理数 $\frac{a}{b}$,其中 $a$ 和 $b$ 互质,且 $b$ 不是 $(10^9 + 7)$ 的倍数。因此你输出的数 $x$ 需要满足 $0 \leq x < 10^9 + 7$ 且 $a \equiv bx \pmod{10^9 + 7}$,可以证明这样的 $x$ 唯一存在。
【输入格式】
本题有多组测试数据。输入的第一行两个整数 $c, T$,分别表示测试点编号和测试数据组数,接下来输入每组测试数据。样例满足 $c = 0$。
对于每组测试数据,第一行两个整数 $n, m$,分别表示图 $G$ 的点数和边数,接下来 $m$ 行,第 $i$ ($1 \leq i \leq m$) 行三个整数 $u_i, v_i, w_i$,描述图 $G$ 上的一条边。
【输出格式】
对于每组测试数据,输出一行一个整数,表示图 $G'$ 的最小外向生成树存在且其边权和等于图 $G$ 的最小生成树边权和的概率,对 $(10^9 + 7)$ 取模。
【样例输入】
0 2 2 1 1 2 1 3 3 1 2 2 1 3 2 2 3 2
【样例输出】
750000006 171875002
【样例说明】
该组样例共有 2 组测试数据。
- 对于第一组测试数据,由于图上只有一条边,因此只要 $G'$ 上有边,$G'$ 的最小外向生成树边权和就一定等于 $G$ 的最小生成树边权和。$G'$ 上存在边的概率为 $\frac{3}{4}$,故答案为 $\frac{3}{4}$,取模后的结果为 $750\,000\,006$。
- 对于第二组测试数据,在所有 $2^{2m} = 64$ 种 $G'$ 中,有 13 种情况不满足 $G'$ 的最小外向生成树边权和等于 $G$ 的最小生成树边权和:
- $G'$ 为空图;
- $G'$ 仅包含一条有向边,共 6 种情况;
- $G'$ 仅包含两条有向边,且指向同一个节点,共 3 种情况;
- $G'$ 仅包含两条有向边,且构成一个二元环,共 3 种情况。
由于所有情况等概率出现,因此答案为 $1 - \frac{13}{64} = \frac{51}{64}$,取模后的结果为 $171\,875\,002$。
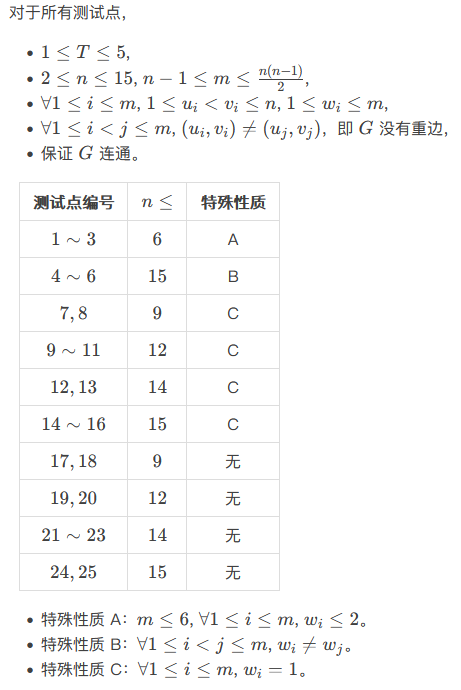
【数据规模与约定】
【来源】
2025联合省选day2T2