| 题目名称 | 2554. 可持久化线段树 |
|---|---|
| 输入输出 | longterm_segtree.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:160, 提交:348, 通过率:45.98% | ||||
|
|
100 | 0.090 s | 16.37 MiB | C++ |
|
|
100 | 0.103 s | 17.21 MiB | C++ |
|
|
100 | 0.113 s | 28.96 MiB | C++ |
|
|
100 | 0.120 s | 12.12 MiB | C++ |
|
|
100 | 0.144 s | 137.77 MiB | C++ |
|
|
100 | 0.156 s | 23.58 MiB | C++ |
|
|
100 | 0.162 s | 39.65 MiB | C++ |
|
|
100 | 0.162 s | 114.81 MiB | C++ |
|
|
100 | 0.165 s | 23.65 MiB | C++ |
|
|
100 | 0.168 s | 15.58 MiB | C++ |
| 关于 可持久化线段树 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
| ||||
|
回复 @Hzoi_QTY :
指针不是消耗空间更大吗?
2018-02-24 22:10
18楼
| ||||
|
友情提示:数组的话内存只需要开$O(N+MlogN)$即可。
(有人能告诉我你们为啥都用指针吗?) 计算器是个好东西(划掉
2018-02-24 22:07
17楼
| ||||
|
算错内存。。
| ||||
|
% 各位会主席树的大佬 菜鸡并不会
2017-10-01 06:14
15楼
| ||||
|
回复 @Hzoi_Mafia :
怕MLE用指针就行了。 | ||||
|
回复 @Hzoi_Mafia :
%%%王超神 | ||||
|
回复 @Hzoi_QTY :
强强强 | ||||
|
我竟然沦落到水这种题都$MLE$了
我可能是废了 | ||||
|
自己脑洞的可持久化线段树,因为缺乏理论指导,代码丑的要死
2017-09-05 09:55
10楼
| ||||
【题目描述】
为什么说本题是福利呢?因为这是一道非常直白的可持久化线段树的练习题,目的并不是虐人,而是指导你入门可持久化数据结构。
线段树有个非常经典的应用是处理$ RMQ $问题,即区间最大/最小值询问问题。现在我们把这个问题可持久化一下:
"$Q$ $k$ $l$ $r$" 查询数列在第$ k $个版本时,区间$ [l, r] $上的最大值
"$M$ $k$ $p$ $v$" 把数列在第$ k $个版本时的第$ p $个数修改为$ v $,并产生一个新的数列版本
最开始会给你一个数列,作为第$ 1 $个版本。
每次$ M $操作会导致产生一个新的版本。修改操作可能会很多呢,如果每次都记录一个新的数列,空间和时间上都是令人无法承受的。所以我们需要可持久化数据结构:

对于最开始的版本 1 ,我们直接建立一颗线段树,维护区间最大值。
修改操作呢?我们发现,修改只会涉及从线段树树根到目标点上一条树链上logn个节点而已,其余的节点并不会受到影响。所以对于每次修改操作,我们可以只重建修改涉及的节点即可。就像这样:
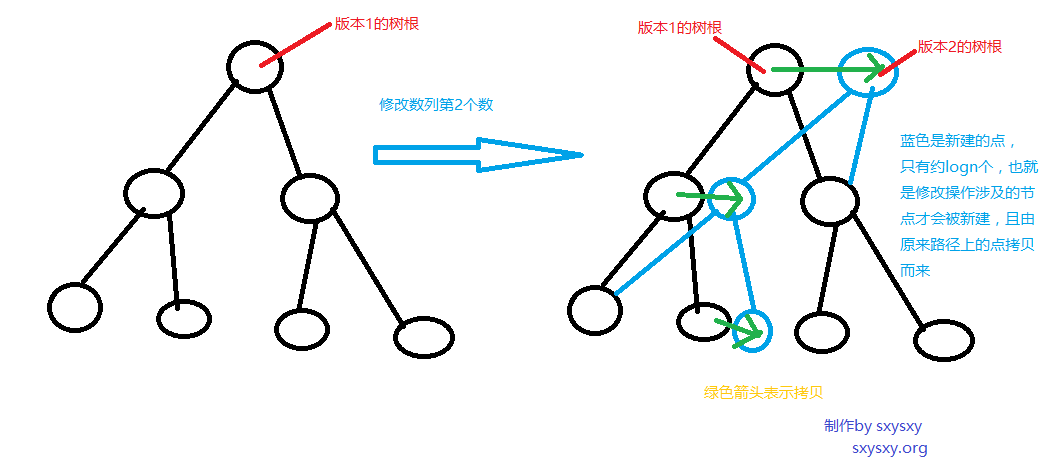
需要查询第$ k $个版本的最大值,那就从第$ k $个版本的树根开始,像查询普通的线段树一样查询即可。
要计算好所需空间哦
【输入格式】
第一行两个整数$ N, Q $。$ N $是数列的长度,$ Q $表示询问数
第二行$ N $个整数,是这个数列
之后$ Q$行,每行以 0 或者 1 开头,0 表示查询操$ Q $,$ 1 $表示修改操作$ M $,格式为
"$0$ $k$ $l$ $r$" 查询数列在第$ k $个版本时,区间$ [l, r] $上的最大值 或者
"$1$ $k$ $p$ $v$" 把数列在第$ k $个版本时的第$ p $个数修改为$ v $,并产生一个新的数列版本
【输出格式】
对于每个$ M $询问,输出正确答案
【样例输入】
4 5 1 2 3 4 0 1 1 4 1 1 3 5 0 2 1 3 0 2 4 4 0 1 2 4
【样例输出】
4 5 4 4
【提示】
序列版本 1 : 1 2 3 4 ,
查询版本 1 的$ [1, 4] $最大值为 4;
修改产生版本 2 : 1 2 5 4 ,
查询版本 2 的$ [1, 3] $最大值为 5;
查询版本 1 的$ [4, 4] $最大值为 4;
查询版本 1 的$ [2, 4] $最大值为 4.
【数据范围】
对于$100\%$的数据,保证有$N ≤ 1×10^4,Q ≤ 1×10^5 $
对于每次询问操作的版本号$ k $保证合法,
区间$ [l, r] $一定满足$ 1 ≤ l ≤ r ≤ N $。
【来源】
神$boy♂$出题人: sxysxy。原题见: http://syzoj.com/problem/247