| 题目名称 | 3954. [NOIP 2023]三值逻辑 |
|---|---|
| 输入输出 | tribool.in/out |
| 难度等级 | ★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:2, 提交:12, 通过率:16.67% | ||||
|
|
100 | 0.730 s | 4.78 MiB | C++ |
|
|
100 | 1.614 s | 4.78 MiB | C++ |
|
|
40 | 1.789 s | 8.04 MiB | C++ |
|
|
40 | 1.794 s | 7.96 MiB | C++ |
|
|
40 | 1.849 s | 7.96 MiB | C++ |
|
|
30 | 1.755 s | 7.99 MiB | C++ |
|
|
20 | 1.715 s | 4.68 MiB | C++ |
|
|
20 | 1.753 s | 8.25 MiB | C++ |
|
|
20 | 1.849 s | 8.25 MiB | C++ |
|
|
0 | 0.028 s | 3.67 MiB | C++ |
| 关于 三值逻辑 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
这题太吃操作了
2025-10-11 20:09
1楼
| ||||
【题目描述】
小 L 今天学习了 Kleene 三值逻辑。
在三值逻辑中,一个变量的值可能为:真($True$,简写作 $T$)、假($False$,简写作$F$)或未确定($Unknown$,简写作 $U$)。
在三值逻辑上也可以定义逻辑运算。由于小 L 学习进度很慢,只掌握了逻辑非运算¬,其运算法则为:
$\lnot{}T=F,\lnot{}F=T,\lnot{}U=U$.
现在小 L 有 $n$ 个三值逻辑变量 $x_1,\cdots,x_n$。小 L 想进行一些有趣的尝试,于是他写下了 $m$ 条语句。语句有以下三种类型,其中$\leftarrow$表示赋值:
1.$x_i\leftarrow v$,其中 $v$ 为 $T, F, U$ 的一种;
2. $x_i\leftarrow x_j$;
3. $x_i\leftarrow{}\lnot{}x_j$。
一开始,小 L 会给这些变量赋初值,然后按顺序运行这 $m$ 条语句。
小 L 希望执行了所有语句后,所有变量的最终值与初值都相等。在此前提下,小 L希望初值中 $Unknown$ 的变量尽可能少。
在本题中,你需要帮助小 L 找到 $Unknown$变量个数最少的赋初值方案,使得执行了所有语句后所有变量的最终值和初始值相等。小 L 保证,至少对于本题的所有测试用例,这样的赋初值方案都必然是存在的。
【输入格式】
本题的测试点包含有多组测试数据。
输入的第一行包含两个整数 $c$ 和 $t$,分别表示测试点编号和测试数据组数。对于样例,$c$ 表示该样例与测试点 $c$ 拥有相同的限制条件。
接下来,对于每组测试数据:
• 输入的第一行包含两个整数 $n$ 和 $m$,分别表示变量个数和语句条数。
• 接下来 $m$ 行,按运行顺序给出每条语句。
– 输入的第一个字符 $v$ 描述这条语句的类型。保证 $v$ 为 TFU+‐ 的其中一种。
– 若 $v$ 为 $TFU$ 的某一种时,接下来给出一个整数 $i$,表示该语句为 $x_i\leftarrow v$;
– 若 $v$ 为 $+$,接下来给出两个整数 $i, j$,表示该语句为$x_i\leftarrow x_j$;
– 若 $v$ 为 $‐$,接下来给出两个整数 $i, j$,表示该语句为$x_i\leftarrow{}\lnot{}x_j$。
【输出格式】
对于每组测试数据输出一行一个整数,表示所有符合条件的赋初值方案中,$Unknown$变量个数的最小值。
【样例输入】
1 3 3 3 ‐ 2 1 ‐ 3 2 + 1 3 3 3 ‐ 2 1 ‐ 3 2 ‐ 1 3 2 2 T 2 U 2
【样例输出】
0 3 1
【样例说明】
第一组测试数据中,$m$ 行语句依次为
• $x_2\leftarrow{}\lnot{}x_1$;
• $x_3\leftarrow{}\lnot{}x_2$;
• $x_1\leftarrow{}\lnot{}x_3$。
一组合法的赋初值方案为 $x_1 =T$, $x_2 = F$, $x3 = T$,共有 $0$ 个 $Unknown$ 变量。因为
不存在赋初值方案中有小于 $0$ 个 $Unknown$ 变量,故输出为 $0$。
第二组测试数据中,$m$ 行语句依次为
• $x_2\leftarrow{}\lnot{}x_1$;
• $x_3\leftarrow{}\lnot{}x_2$;;
• $x_1\leftarrow{}\lnot{}x_3$。
唯一的赋初值方案为 $x_1 = x_2 = x_3 = U$,共有 $3$ 个 $Unknown$ 变量,故输出为 $3$。
第三组测试数据中,$m$ 行语句依次为
• $x_2\leftarrow T$;
• $x_2\leftarrow U$;
一个最小化 Unknown 变量个数的赋初值方案为 $x_1 = T, x_2 = U。x_1 = x_2 = U$ 也是
一个合法的方案,但它没有最小化 $Unknown$ 变量的个数。
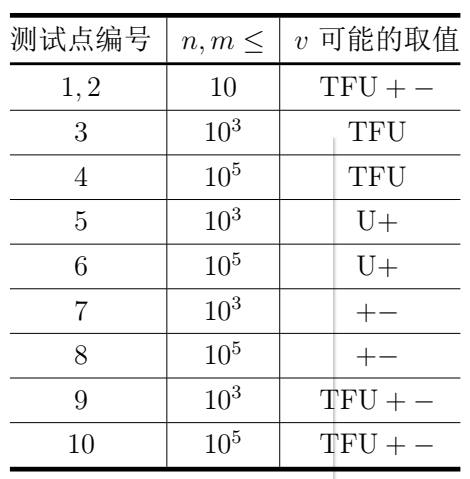
【数据规模与约定】
对于所有测试数据,保证:
• $1\leq t\leq 6,1\leq n,m\leq 10^5$;
• 对于每个操作,$v$ 为 $TFU+‐$ 中的某个字符,$1\leq i,j\leq n$。
【来源】
NOIP 2023 Task2