| 题目名称 | 2308. [CTSC 2016]单调上升路径 |
|---|---|
| 输入输出 | daydayup.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:2, 通过率:0% | ||||
|
|
0 | 0.005 s | 6.71 MiB | C++ |
|
|
0 | 0.049 s | 1.29 MiB | C++ |
| 关于 单调上升路径 的近10条评论(全部评论) |
|---|
【题目描述】
对于一个带权无向图,我们可以考察它的单调上升路径。
一条路径被称为单调上升的,如果沿着它走时权值是单调递增的。
注意,路径由多条首尾相连的边组成,且可经过同一顶点多次。路径的长度为它包含的边数。
举例来说:下图中 v2 -> v4 -> v1 -> v2是一条单调上升路径,因为每条边的权值依次为 1,2,4。这条路径的长度为 3。更进一步的,你可以验证下图中所有的单调上升路径的长度都不超过 3。
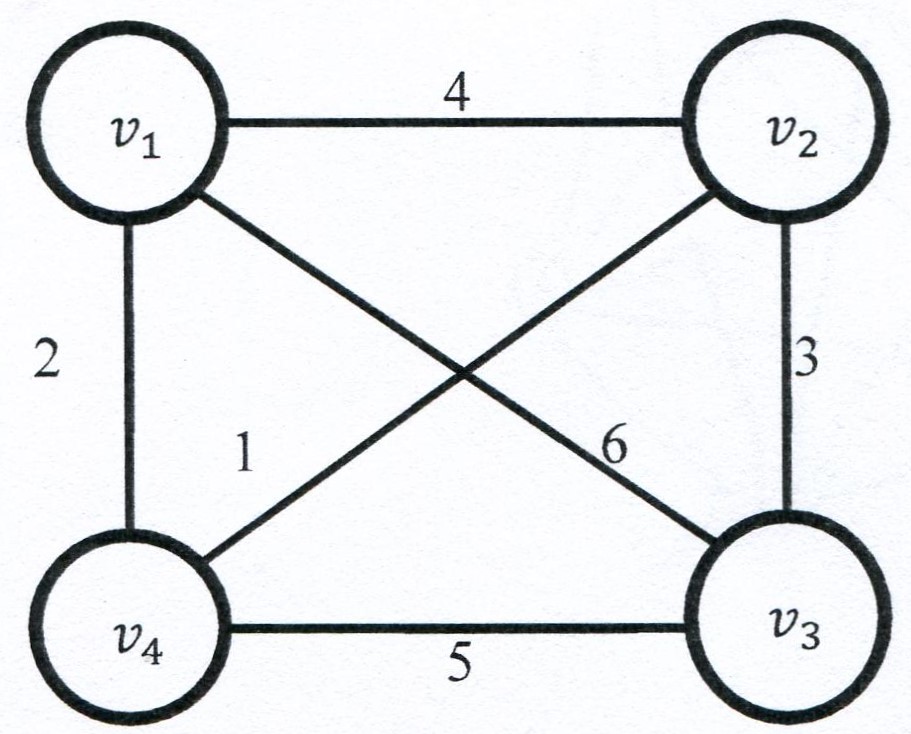
下面的结论指出在某些图中总会存在一个比较长的单调上升路径:
结论:假设带权无向图 G 有 100 个节点 1000 条边,且所有权值各不相同。那么,G 中一定存在一个单调上升路径,它的长度大于等于 20。
证明:假设每个节点上有一个探险家。我们按权值从小到大枚举所有的边,每次将该边连接的节点中的探险家的位置进行对调。可以知道,每个探险家都走的是一条单调上升路径。另外,由于共有 100 个探险家,而探险家一共走了 2000 步,所以有人走了 20 步。证毕。
现在,我们的问题是:
给定一个完全图 G,它的顶点个数为一个偶数 N。
你的任务是给每条边选一个不同的权值,要使得最长的单调上升路径最短。
【输入格式】
输入仅一行一个正偶数 N。
【输出格式】
输出整数1到 N*(N-1)/2 的一个排列,相邻的数之间用一个空格或换行隔开。
第一个数代表你给边 (1,2) 选的权值;第二个数是给 (1,3) 的权值,……,第 N 个数是 (1N) 的权值;然后是 (2,3) 的权值,(2,4) 的权值,……,(2,N)的权值;然后是 (3,4) 到 (3,N) 的权值;以此类推;最后是(N-1,N) 的权值。
【样例输入1】
4
【样例输出2】
4 6 2 3 1 5
【样例输入1】
6
【样例输出】
12 8 15 3 5 6 7 1 13 10 14 11 4 2 9
【子任务及部分分】
对于 20%的数据,满足 2 ≤ N ≤ 20;
对于 50%的数据,满足 2 ≤ N ≤100;
对于 100%的数据,满足 2 ≤ N ≤500。
除不同的测试点有不同特点外,每个测试点你也可能获得部分分。如果你的程序能正确结束并按输出格式输出,我们将用下列方式评分:
假设你的图中最长单调上升路径的长度为 A,正确答案为 B。
如果 A = B,你的得分为 10 分;
如果 B < A < 2*B,你的得分为 3 分;
如果 A ≥ 2*B,你的得分为0分。
【来源】
CTSC2016 D2T1
(原题目中提供了额外的一份文件,由于COGS的限制,暂不提供)