|
|
×
提示!该题解未通过审核,建议分享者本着启发他人,照亮自己的初衷以图文并茂形式完善之,请勿粘贴代码。#include<bits/stdc++.h> using namespace std; int main() { freopen("poker.in","r",stdin);
freo 该题解等待再次审核........................................................................(剩余 821 个中英字符)
题目4049 [CSP 2024 J]扑克牌
2024-11-04 18:15:34
|
|
|
题目3055 [NOIP 2018]赛道修建
 2
评论 2
评论
2024-10-24 23:23:50
|
|
|
 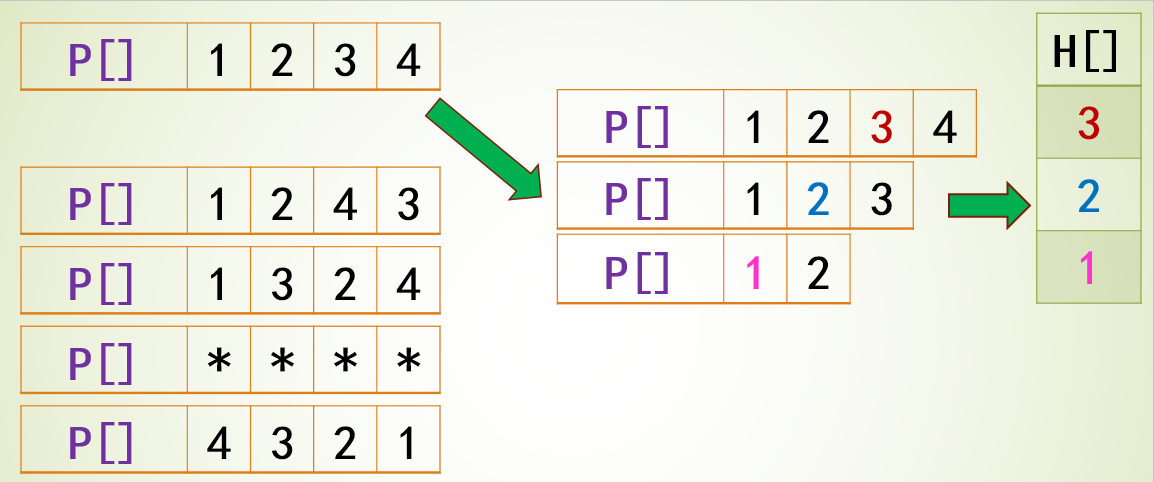  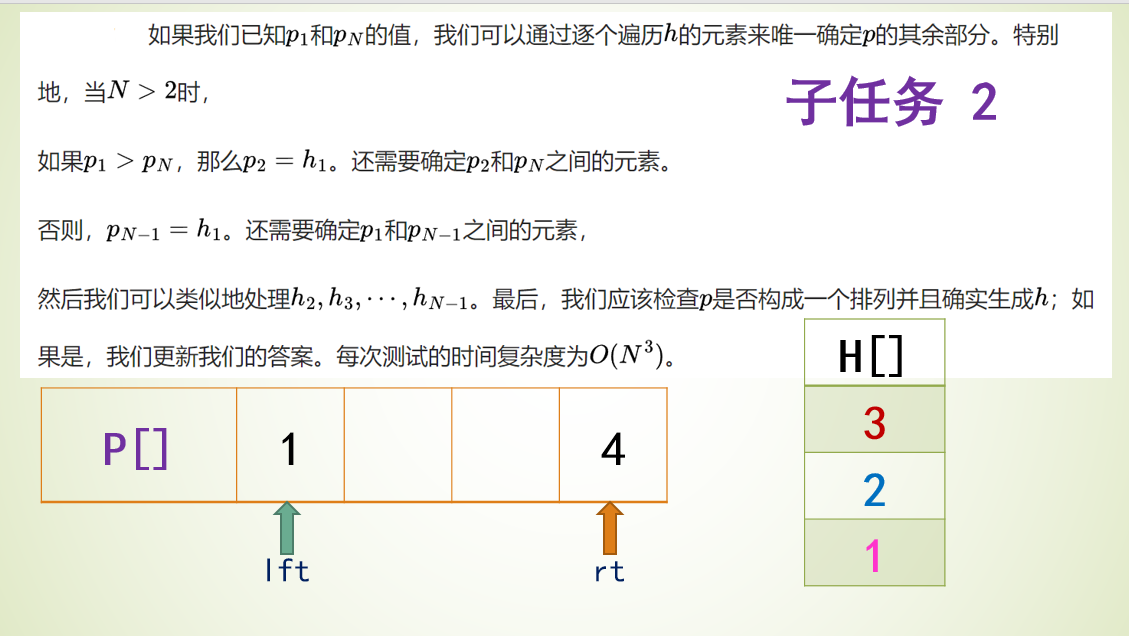 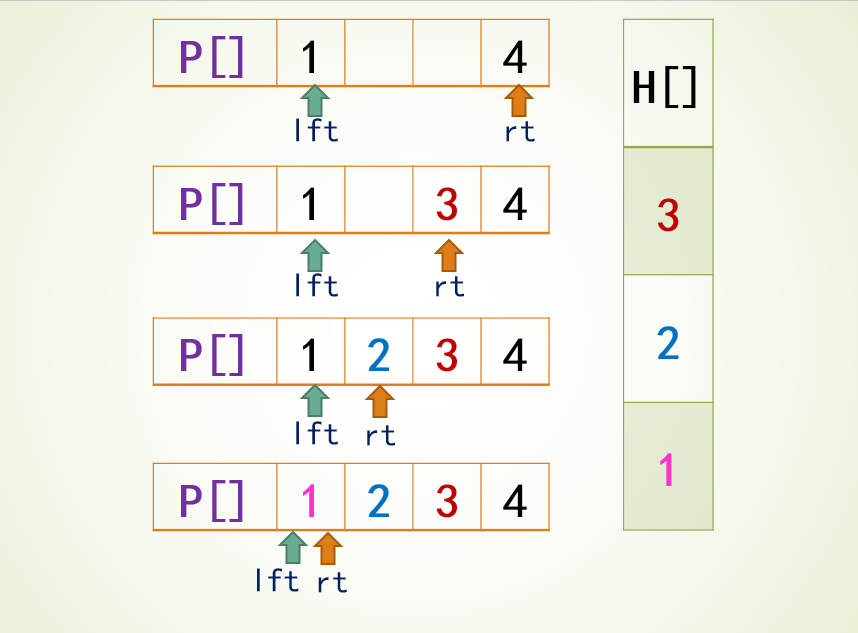  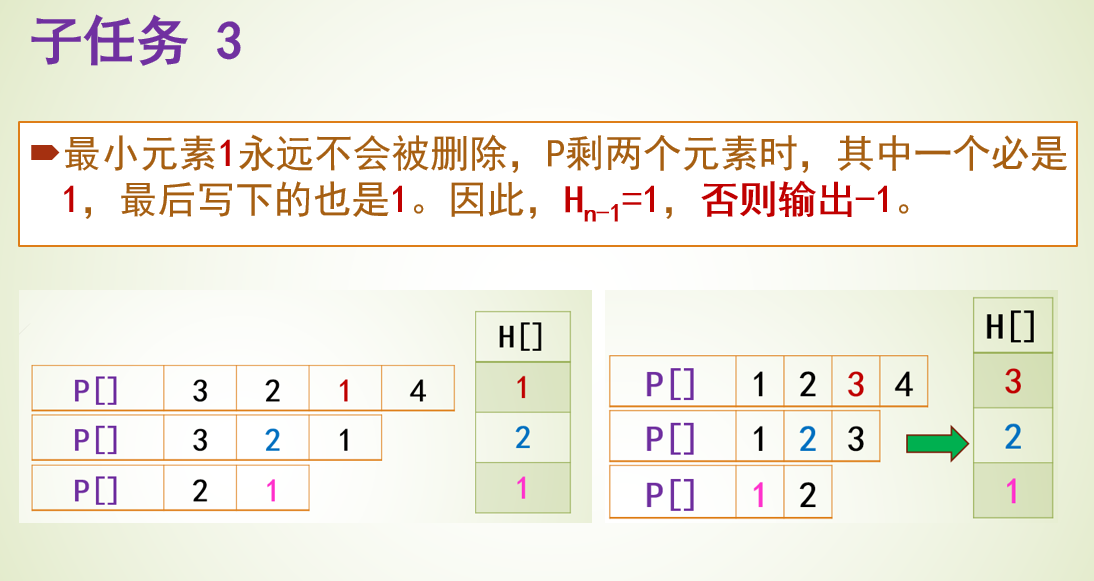 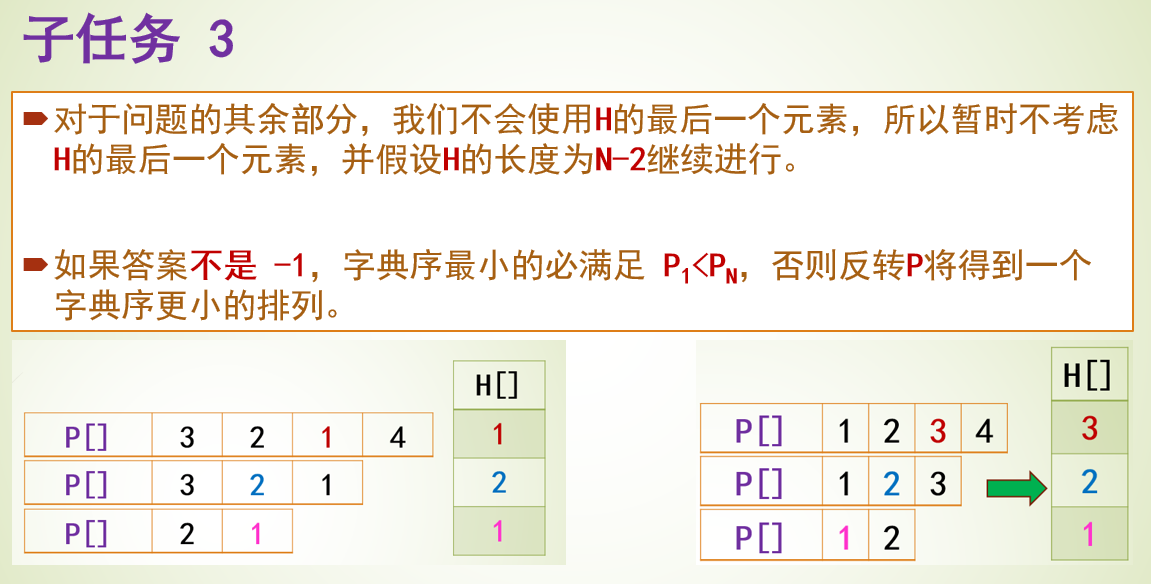   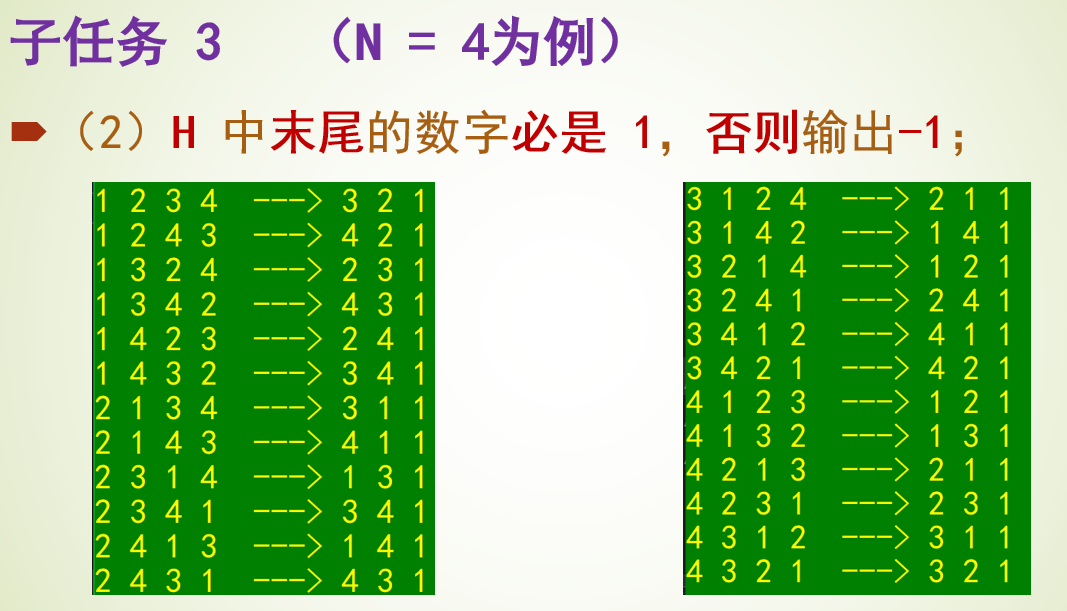      
题目4031 [USACO24 Open Bronze]Farmer John’s Favorite Permutation
 2
评论 2
评论
2024-10-24 12:32:02
|
|
|
CSP 2022J 解密 题解首先分析题目对于给定的 $n$,$e$,$d$,询问是否存在一组正整数 $p$,$q$ 满足 $pq=n$ 且 $(p-1)(q-1)+1=ed$。 S.1考虑暴力。 枚举每组 $pq=n$,检查是否满足 $(p-1)(q-1)+1=ed$。 时间复杂度 $O(k\sqrt{n})$,预计20pts(但实际上40pts)。 S.2(正解)注意到 $n$ 的范围特别大,考虑分析题目的式子。 $$(p-1)(q-1)+1=ed$$ $$pq-p-q+2=ed$$ $$n-p-q+2=ed$$ $$n-ed+2=p+q$$ 令 $m=n-ed+2$。 结合上面的 $pq=n$,注意到这是一个方程。 尝试换元,得到一元二次方程 $p^2-mp+n=0$,只需检验两个根是否都为正整数即可。 时间复杂度 $O(k)$。预计100pts。
题目3778 [CSP 2022J]解密
 4
评论 4
评论
2024-10-09 20:46:13
|
|
|
这道题可以使用分治算法和暴力枚举来解决先写一下分治的思路我们需要找到一个k使得k%n的值在L和R区间内最大。
递归步骤:
要先知道: 如果 L > R,说明区间为空,返回 0。 步骤: 计算中间值 mid。 如果 mid % n 不为 0,则比较 mid % n 和右半边 [mid + 1, R] 的结果,返回较大的值。 如果 mid % n 为 0,则递归地在左半边区间 [L, mid - 1] 查找。 举个栗子
假设 L = 3, R = 10, n = 5 第一次调用 find(3, 10, 5): mid = 6 mid % n = 6 % 5 = 1(非零) 比较 1 和 find(7, 10, 5) 的结果。 第二次调用 find7, 10, 5): mid = 8 mid % n = 8 % 5 = 3(非零) 比较 3 和 find(9, 10, 5) 的结果。 第三次调用 find(9, 10, 5): mid = 9 mid % n = 9 % 5 = 4(非零) 返回 4。 第二次调用返回 3 和 4 比较,返回 4。 第一次调用返回 1 和 4 比较,返回 4。 最终答案为 4。 OK,写个栗子(第一次发题解,用ai再给我改了一遍)
// 计算按照规则分糖果后剩余的数量 int jisuan(int n, int k) { int shengYu = k; while (shengYu >= n) { shengYu -= n; } return shengYu; } // 分治算法函数 int fenZhiSuanFa(int n, int zuoBian, int youBian) { if (zuoBian == youBian) { return jisuan(n, zuoBian); } int zhongJian = (zuoBian + youBian)/2; int shengYu_zhongJian = jisuan(n, zhongJian); int shengYu_zhongJian_jia_1 = jisuan(n, zhongJian + 1); int shengYu_zhongJian_jian_1 = jisuan(n, zhongJian - 1); if (shengYu_zhongJian >= shengYu_zhongJian_jian_1 && shengYu_zhongJian >= shengYu_zhongJian_jia_1) { return shengYu_zhongJian; } else if (shengYu_zhongJian_jian_1 > shengYu_zhongJian) { return fenZhiSuanFa(n, zuoBian, zhongJian - 1); } else { return fenZhiSuanFa(n, zhongJian + 1, youBian); } }
|
|
|
分糖果这道题也是肥肠简单的: 只要找到了规律就可以迎刃而解了 再看题解之前可以先想想自己是怎么写的: [1]模拟分糖果的过程? [2]找规律? 聪明的你一定第一次就想到了要找规律 (第一次用的模拟 事实证明会爆)!!! 那么该怎么做呢? 在分糖果这道题中存在一个下限和上限 也就是L和R 动用那你聪明的小脑瓜就可以发现 如果(if) L/n等于R/n 当这种情况存在的时候 我们的结果就是r%n tip:也就是上限(R)模人数(n) 显而易见的 另外的(else) 也就是说当R/n不等于L/n的时候 我们怎么办呢? 这时候就可以再思考一下下了捏 当这种情况是 也就说明了再上线R和下线L中间一定存在一种剩余糖果最多的情况 所以这种情况的结果就是n-1 tip:也就是人数(n)减去一 显而易见的 那么这道题是不是就迎刃而解了呢! 是的! 代码附上 希望能帮到OIer们 点个赞呗!!!
题目3615 [CSP 2021J]分糖果
AAAAAAAAAA
 7
14 条 评论 7
14 条 评论
2024-10-03 21:40:06
|