更好的阅读体验：https://www.cnblogs.com/To-Carpe-Diem/p/19361912

大意

有 $n+1$ 根柱子（编号 $1 \sim n+1$），其中 $1 \sim n$ 号柱子初始时各有 $m$ 个球（球按**自底向上**的顺序摆放），$n+1$ 号柱子初始为空；所有球共包含 $n$ 种颜色，且每种颜色的球恰好有 $m$ 个。

允许执行的操作是：将某根柱子最上方的球移动到另一根柱子的最上方，操作需满足两个条件：

1. 源柱子（移出球的柱子）非空；

2. 目标柱子（移入球的柱子）上的球数量不超过 $m-1$。

要求通过不超过 $820000$ 次上述操作，使得所有同一种颜色的球都汇聚到同一根柱子上（每种颜色最终对应哪根柱子无限制）。

思路

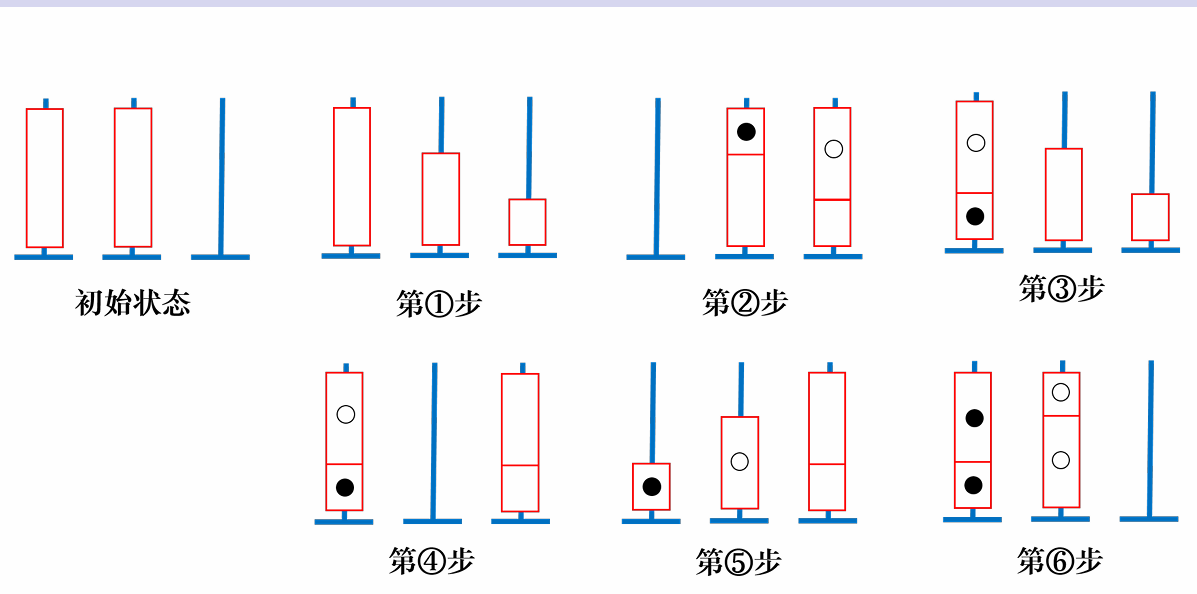
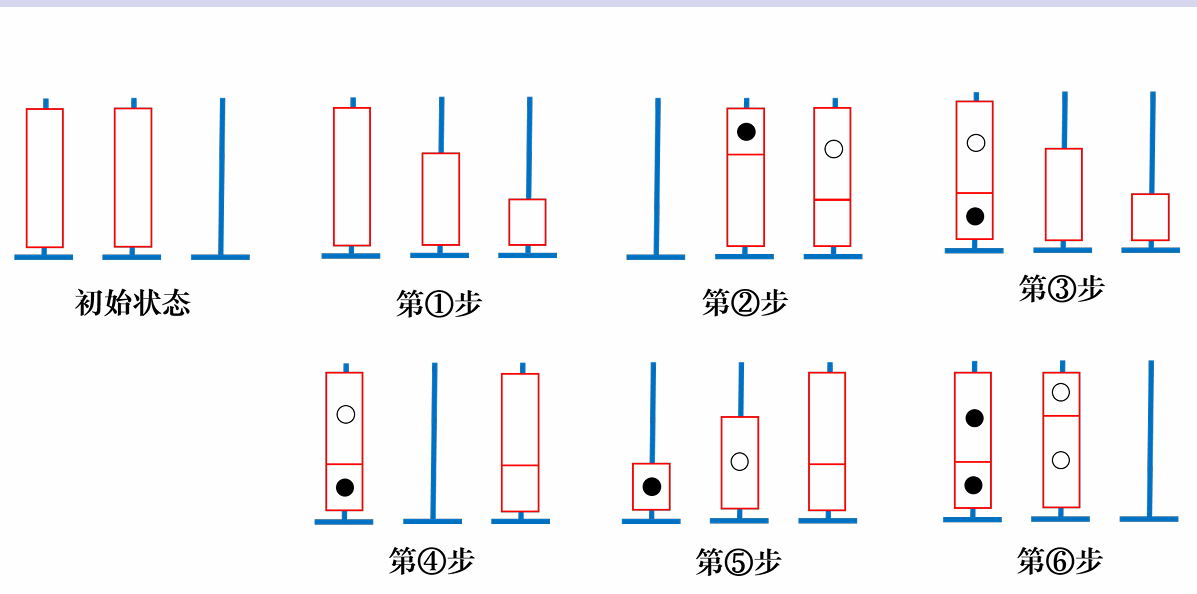
首先，这个题是个构造题，然后我们考虑构造方法，先看特殊性质 $n = 2$ 的时候，也就是说此时只有 $3$ 个柱子和 $2$ 种颜色，那么我们应该怎么去放这个东西呢？

我们将两种颜色用白和黑表示，那么我们很容易想到去分离黑白，如何做呢？如上图，我们先在第二个柱子上空出第一个柱子中黑的个数，这样就可以将第一根柱子黑白分离，再把分离好的放回去，把剩下的没分的整到一根柱子上，再把第一根的黑白分离到两个不同的柱子上，然后把没分离的那根柱子直接按黑白分离即可。

总操作次数是：$5m - k$，$k$ 表示第一个柱子中黑的个数。

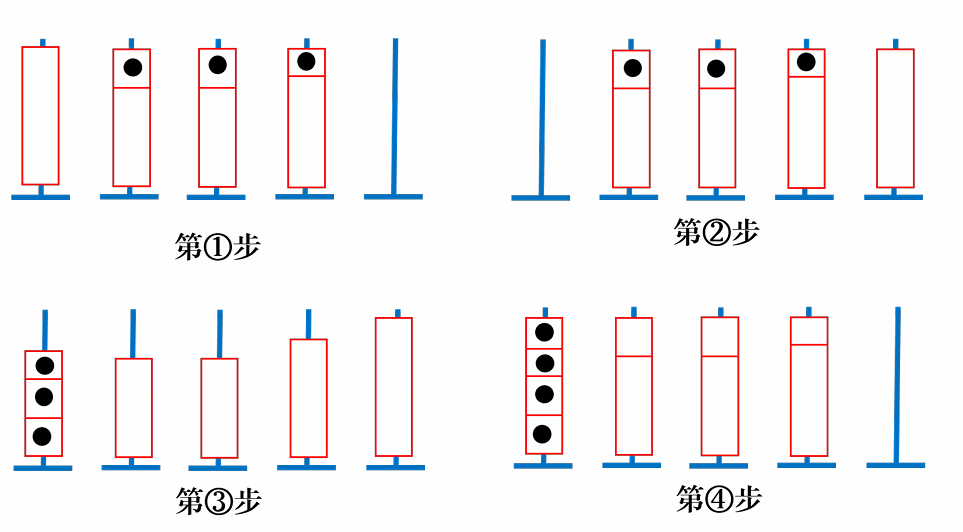
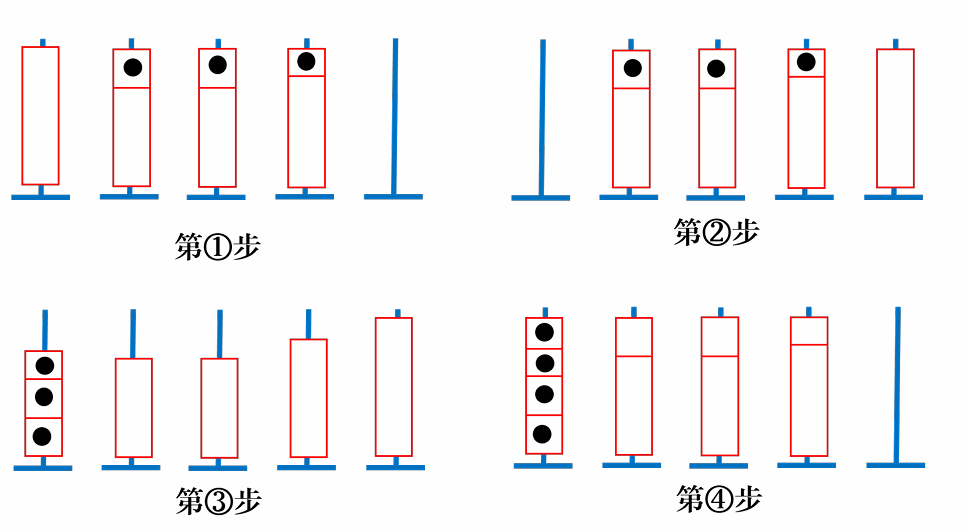
我们继续考虑 $n$ 比较大的时候怎么办，我们可以像刚刚的操作一样，对于每一个颜色 $i \in [1, n]$ 依次操作，对于颜色 $i$，先把 $[i + 1, n]$ 的柱子中的颜色 $i$ 全放在柱头，然后直接如下图进行操作即可：

但是经过计算发现以上的构造方式并不能通过本题，我们需要考虑其他的方法。

考虑分治。

我们发现对于 $n  = 2$ 的情况处理起来很容易，要是全部都能当成两个颜色做就好了，于是我们就可以对于当前处理的区间 $[l, r]$ 进行分治 $[l, mid], [mid + 1, r]$，我们将 $[l, mid]$ 的柱子全部整理成颜色小于等于 mid 的，将 $[mid + 1, r]$ 的柱子全部整理成颜色大于 mid 的，每次分治时，可以 $\mathcal{O}(n ^ 2)$ 的去枚举 $i \in [l, mid], r \in [mid + 1, r]$，对 $i$ 和 $j$ 的颜色整理。如果两个柱子中颜色小于等于 mid 的大于 $m$，就将 $i$ 整理，反之。

因此就解决了这道题。