更好的阅读体验：https://www.cnblogs.com/To-Carpe-Diem/p/19361912

大意

有 $n+1$ 根柱子（编号 $1 \sim n+1$），其中 $1 \sim n$ 号柱子初始时各有 $m$ 个球（球按**自底向上**的顺序摆放），$n+1$ 号柱子初始为空；所有球共包含 $n$ 种颜色，且每种颜色的球恰好有 $m$ 个。

允许执行的操作是：将某根柱子最上方的球移动到另一根柱子的最上方，操作需满足两个条件：

1. 源柱子（移出球的柱子）非空；

2. 目标柱子（移入球的柱子）上的球数量不超过 $m-1$。

要求通过不超过 $820000$ 次上述操作，使得所有同一种颜色的球都汇聚到同一根柱子上（每种颜色最终对应哪根柱子无限制）。

思路

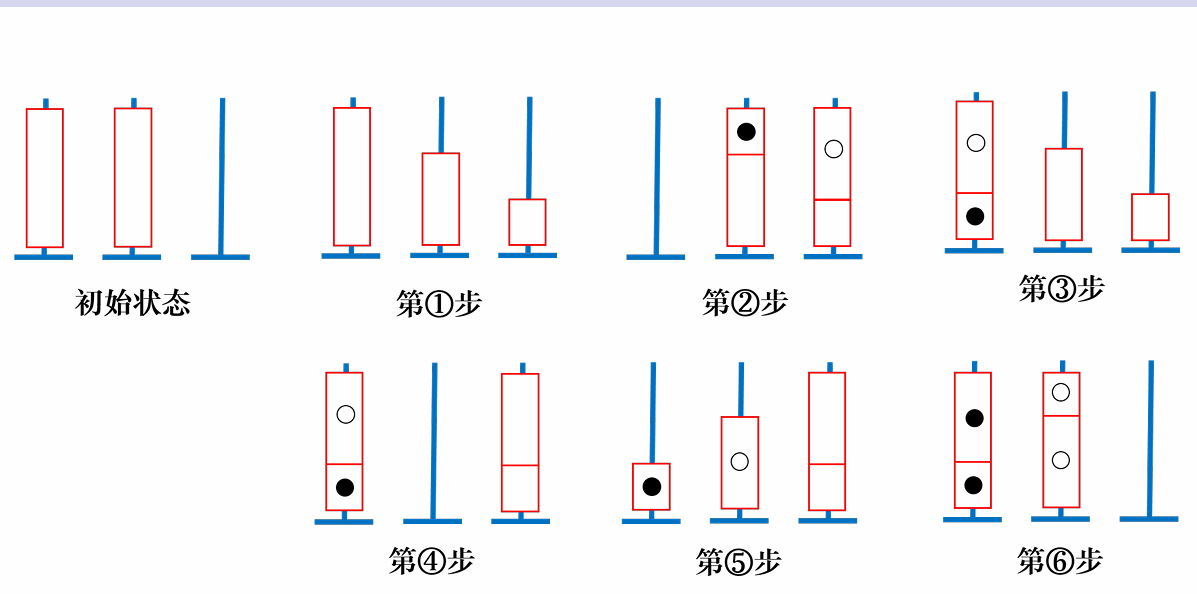
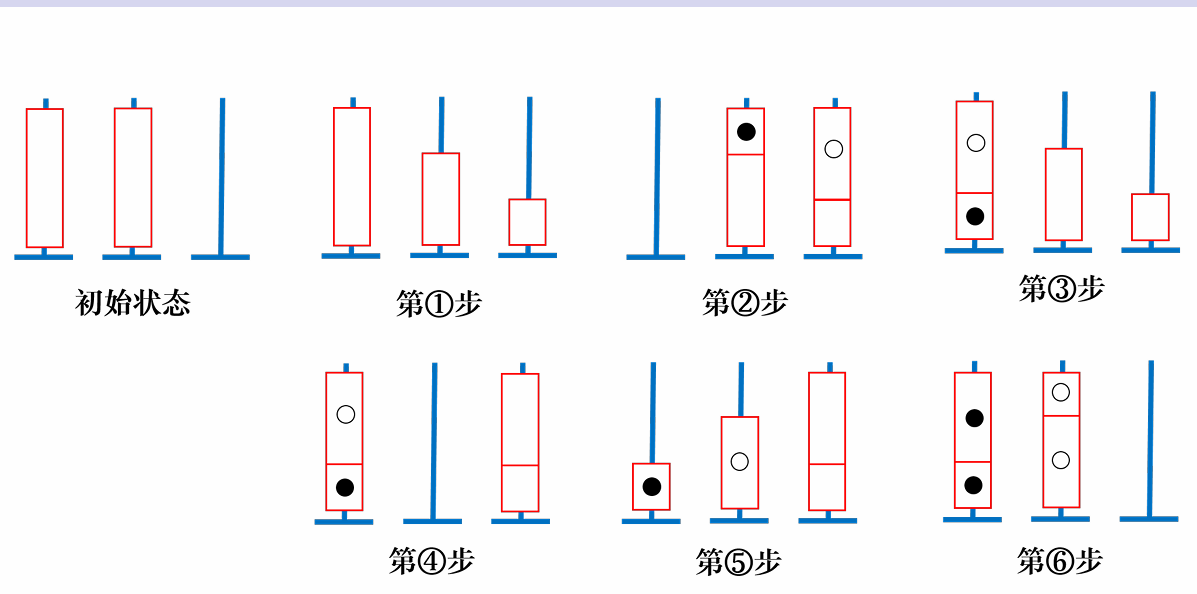
首先，这个题是个构造题，然后我们考虑构造方法，先看特殊性质 $n = 2$ 的时候，也就是说此时只有 $3$ 个柱子和 $2$ 种颜色，那么我们应该怎么去放这个东西呢？

我们将两种颜色用白和黑表示，那么我们很容易想到去分离黑白，如何做呢？如上图，我们先在第二个柱子上空出第一个柱子中黑的个数，这样就可以将第一根柱子黑白分离，再把分离好的放回去，把剩下的没分的整到一根柱子上，再把第一根的黑白分离到两个不同的柱子上，然后把没分离的那根柱子直接按黑白分离即可。

总操作次数是：$5m - k$，$k$ 表示第一个柱子中黑的个数。

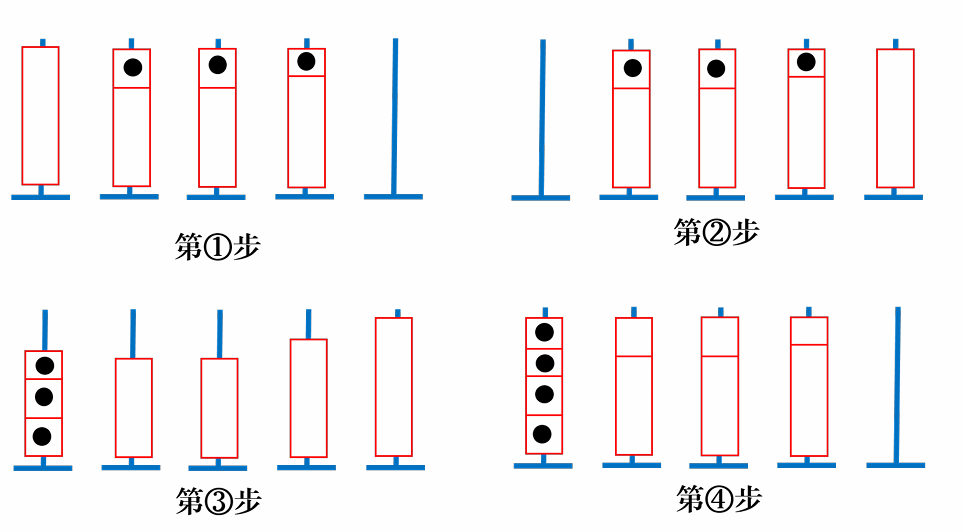
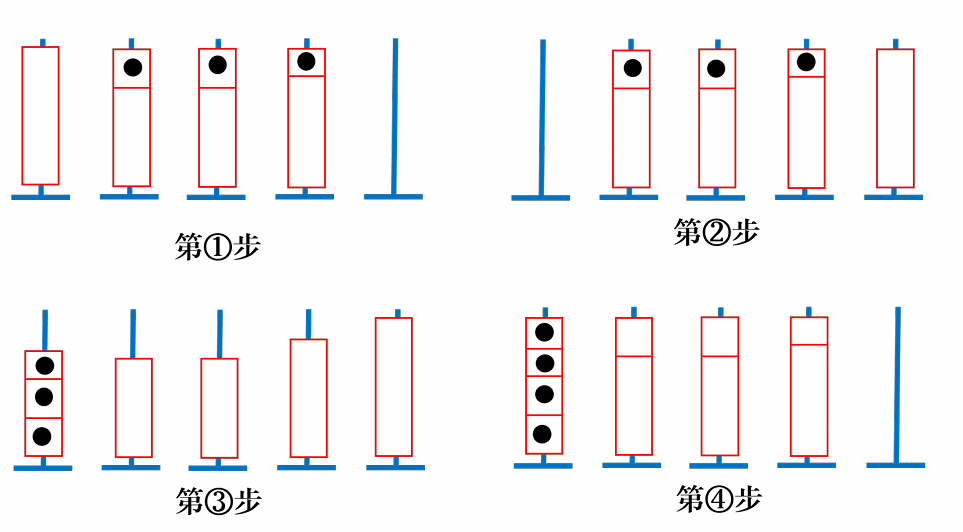
我们继续考虑 $n$ 比较大的时候怎么办，我们可以像刚刚的操作一样，对于每一个颜色 $i \in [1, n]$ 依次操作，对于颜色 $i$，先把 $[i + 1, n]$ 的柱子中的颜色 $i$ 全放在柱头，然后直接如下图进行操作即可：

但是经过计算发现以上的构造方式并不能通过本题，我们需要考虑其他的方法。

考虑分治。

我们发现对于 $n  = 2$ 的情况处理起来很容易，要是全部都能当成两个颜色做就好了，于是我们就可以对于当前处理的区间 $[l, r]$ 进行分治 $[l, mid], [mid + 1, r]$，我们将 $[l, mid]$ 的柱子全部整理成颜色小于等于 mid 的，将 $[mid + 1, r]$ 的柱子全部整理成颜色大于 mid 的，每次分治时，可以 $\mathcal{O}(n ^ 2)$ 的去枚举 $i \in [l, mid], r \in [mid + 1, r]$，对 $i$ 和 $j$ 的颜色整理。如果两个柱子中颜色小于等于 mid 的大于 $m$，就将 $i$ 整理，反之。

因此就解决了这道题。

更好的阅读体验：https://www.cnblogs.com/To-Carpe-Diem/p/19354572

给定一棵有 $n$ 个节点的树，巡警车从 $1$ 号节点出发遍历所有边后返回，每条边需经过两次，总距离为 $2*(n-1)$。现可新建 $K$ 条边$(k = \{ 1, 2\})$，要求新建的每条边必须恰好经过一次，求规划新建边的方案，使得巡警车的总巡逻距离最小，并输出该最小值。

我们可以发现，对于 $k = 1$ 的情况，显然你求出一条直径，再把直径的两个端点连上，这样是最优的。

但是当 $k = 2$ 的时候，我们需要再连一次，但是这样的话，我们最好选比较长的，最初的想法是选次长的直径，但是我们想想，如果你选的这条新的直径，和原来的直径，有很多重合的点，那么就不是很优，我们为了处理这个重复的玩意，其实可以把原直径的所有边赋为 $-1$，这样的话，我们再找最长的直径，就不会出问题了。

但是这样需要知道一个问题， dfs 求直径是无法解决边权为负的情况，于是我们考虑树形 dp 的方式，直接再记一次直径的长度即可。

设两次的直径长度为 $L_1, L_2$，则最终答案为：

$k = 1$ 时：$2 * (n - 1) - L_1 + 1$

$k = 2$ 时：$2 * (n - 1) - (L_1 - 1) - (L_2 - 1)$

更好的阅读体验：https://www.cnblogs.com/To-Carpe-Diem/p/19349977

由于题目的数据范围，我们可以得知，大概是个 $n ^ 3$ 的玩意。

但是我们需要仔细想想怎么计数？

首先，这个玩意和什么有关?

第一肯定是步数，第二是点是否走过，第三是这个点和为我们要的强连通图的关系。

然后我们考虑最难的问题，就是这个强连通图怎么判断，怎么累加答案？我们走到一个点的时候怎么判断其是否能与原来的形成一个强连通呢？还是说其目前自己和其他点成强连通，需要后续的操作去整。

不难发现，其实一个点，其强连通关系只有两种，第一种就是和起点在一个强连通里面，第二种，就是不在起点的强连通里面。

我们定义 $f_{i, j, k}$ 表示目前已经走了 $i$ 步，已经访问了 $j$ 个点，与起点 $1$ 形成的强连通的大小为 $k$。（以下所说的形成强连通均是与 $1$ 形成）

考虑转移。

首先走到点，第一种情况，是没有走过，于是我们有：

$f_{i + 1, j + 1, k} \to f_{i + 1,j + 1, k} + f_{i, j, k} \times (n - j)$

第二种，是走过，但是没有形成强连通的点：

$f_{i + 1, j, k} \to f_{i + 1, j, k} + f_{i, j, k} \times (j - k)$

第三种是，走过，且已经形成了强连通：

$f_{i + 1, j, k} \to f_{i + 1, j, k} + f_{i, j, k} \times k$

于是我们的答案就在 $f_{m, n, n}$。

先考虑一下朴素的 dp。

不难发现，对于一个集合最重要的是集合里最小的元素，剩下的元素对应的 $a_i$ 都大于这个值，可以考虑把所有值按照从大到小排序，则集合里其他元素都在最小元素之前。

对于第 $i$ 个数，考虑这个数是集合里最小的元素，或不是最小的元素对应的方案数。 $dp_{i,j}$ 表示 $1\sim i-1$ 个数处理完后，还剩下 $j$ 个数未确定属于哪个集合的方案数。

若第 $i$ 个数不是集合里最小的元素：

$$dp_{i+1,j+1}\gets dp_{i,j}$$

若第 $i$ 个数是集合里最小的元素，枚举这个集合里还有几个元素，即：

$$dp_{i+1,j-k}\gets dp_{i,j}\times \text{C}_j^k(0\le k<a_i)$$

初始状态为 $dp_{1,0}=dp_{1,1}=1$，目标状态为 $dp_{n+1,0}$。转移的过程中对于第二类转移需要枚举 $k$，复杂度为 $O(n^3)$。

考虑如何优化这个 dp 的第二类转移，将组合数拆开得到：

$$dp_{i+1,j-k}\gets dp_{i,j}\times \frac{j!}{k!(j-k)!}$$

假定对于阶段 $i$，设有

$$F(x)=\sum_{i>0}dp_{i,j}j!x^j$$

$$G(x)=\sum_{i>0}\frac{1}{k!}x^j$$

实际上是将 $F,G$ 做一个减法卷积的到 $H$，则有

$$H(x)=\sum_{i>0}dp_{i+1,j}j!x^j$$

对于减法卷积，可以翻转一个多项式的次数，此时减法卷积就转化成了加法卷积，直接用 NTT 计算即可。

可以选择为 $dp_{i,j}$，也可以直接维护 $dp_{i,j}\times j!$。算法的复杂度为 $O(n^2\log n)$。

好像是 COGS 首 A，写篇题解。

其实这道题的思维难度不是特别大，只需要一些技巧和比较高级的算法即可解决。

思路分析

注意到对于一对用来替换的字符串二元组 $(s,t)$，若 $s=t$，则这对字符串一定没用，题目已经限制。

对于这对 $s,t$，可以分别将其表示成 $s=s_A+s_C+s_B,t=t_A+t_D+t_B$，其中 $s_A,t_A$ 是 $s,t$ 的最长公共前缀，$s_B,t_B$ 是 $s,t$ 的最长公共后缀，每次替换操作，实际上是将一个字符串中的 $s_C$ 替换成了 $t_D$。

对于一对询问的字符串 $(S,T)$，若长度不相等，则一定没有合法的变化，题目已经限制。

依然求出两个 $S,T$ 的子串 $s_{A,C,B},t_{A,D,B}$（意义同上），若 $(S,T)$ 可以用过 $(s,t)$ 替换得来，必须满足 $S_C=s_C,T_D=t_D$，且 $s$ 在 $S$ 中出现，$t$ 在 $T$ 中出现。

这样的话，我们就可以得到一个 $O(nq)$ 的算法，对于每个变化的字符串二元组和询问，处理出变化的部分，若 $(s,t),(S,T)$ 变化的部分一样，且 $s$ 再 $S$ 中出现，$t$ 在 $T$ 中出现，因为变化的部分要匹配上，所以匹配的起始位置是确定的，可以用字符串 Hash 来完成 $O(1)$ 的判断。

cin>>S>>T;int ans=0;
if(S.size()!=T.size()){
    printf("0\n");
    continue;
}
int L=0,R=S.size()-1;
while(S[L]==T[L])L++;
while(S[R]==T[R])R--;
for(int j=0;j<S.size();j++){
    if(j){
        hs[j]=hs[j-1]*P+S[j];
        ht[j]=ht[j-1]*P+T[j];
    }else{
        hs[j]=S[j];
        ht[j]=T[j];
    }
}
for(int j=1;j<=n;j++){
    bool flag=0;
    if(l[j]==-1)continue;
    if(R-L+1!=r[j]-l[j]+1)continue;
    int ll=L-l[j],rr=ll+len[j]-1;
    if(ll<0||rr>=S.size())continue;
    if(askS(ll,rr)!=a[j])continue;
    if(askT(ll,rr)!=b[j])continue;
    ans++;
}
printf("%d\n",ans);

考虑优化这个过程，离线，还是利用字符串 Hash，把变化部分相同的变化字符串和询问字符串放在一起处理。

此时变化部分的匹配一定满足，只需要保证 $s_A$ 是 $S_A$ 的后缀，$t_B$ 是 $T_B$ 的前缀。将所有 $s_A,S_A$ 放在一起建一个字典树，$t_B,T_B$ 放在一起建一个字典树，则前后缀关系可以转化成字典树上的祖先子孙关系，两个字典树就有两维的限制，直接做离散化加二维数点即可，复杂度为 $O(L+(n+q)\log(n+q))$。

这个做法所使用的算法均在提高级的考纲之内，应该是钦定的正解。

其实有一种更加优秀的做法，可以转化为经典的多模式串匹配的算法，但需要 AC 自动机。

考虑将每个字符串对 $(s,t)$ 拼成一个大串 $P=s_A+?+s_C+t_D+?+s+B$，其中 $?$ 是防止匹配的一个字符。把询问串也这样拼成大串 $Q$，每个询问就是有多少个 $P$ 是 $Q$ 的子串，直接 AC 自动机的复杂度为 $O(|\sum|L)$，其中 $|\sum|$ 是一个 $26$ 的常数。

后者实现比较简单，所以我只完成了第二个算法。

无法接受自己sT1T2没写出来

UPD 老师已经开大时间限制 已加上第二次评测的记录

我在写这篇题解的时候cogs上时间限制还是1秒，cogs评测机显然不符合CCFIntel Core Ultra 9 285K CPU @ 3.70 GHz的标准，在洛谷和云斗AC的代码，再加上卡常也88分，最慢的1.099s，所以我打扰了老师开大时限，但老师可能比较忙没有回复，所以这篇题解在cogs上的分数按照1s为准。

题意

给你一张$N$个点无向图，保证任意两个点之间都是联通的。

另外还有$K$个额外的点，你可以从这$K$个点里任意选择若干个点，选择第$j$个点的代价为$c_j$，然后对于每个选择的点都可以往原本$N$个点连无向边，第$j$个额外点对第$i$个原有点连边的代价为$a_{j,i}$。

现在求出这张图的MST。

$1 \leq N \leq 10^4$

$1 \leq M \leq 10^6$

$0 \leq K \leq 10$

思路

考场淘汰回放：

把T1当成dp死做半天做不出来之后看第二题，一眼看第二题，先写出了60分左右的解法，代码还写了半天，结果一直以为和最短路有什么关系，恶心半天写不出来了

40~60分

直接把所有的边放到图里，包括额外点的连边。

排序所有边之后，枚举选额外点的状态跑kruskal即可。

粗略估计时间复杂度$O(2^k * (M+NK))$（一共会有$M+NK$条边，枚举状态$2^k$）

不是满分，来看我回忆代码，不加赛时卡常，在cogs上就32分 云斗上80分 洛谷上88分

UPD:开大时间限制后cogs80分

http://218.28.19.228:8081/cogs/submit/code.php?id=7XieaPkPU

https://www.yundouxueyuan.com/record/69072490b8ccc474dc719cef

https://www.luogu.com.cn/record/245035597

100分

我们最终选的边肯定包括了不考虑额外点的最小生成树里，所以先对原图跑一遍最小生成树，只保留树边，然后再枚举状态跑kruskal其实就做完了。

时间复杂度$O(M log M + 2 ^ k * (N - 1 + NK))$

目前卡常在cogs88分，洛谷和云斗不卡常就是满分

UPD:100分了