|
|
Pro894 追查坏牛奶 题解COGS的这一题是超级满配版本 比洛谷的要强力的多:894. 追查坏牛奶 - COGS 额外要求是:求出最小割流量,同时求出割边最小,同时字典序最小的方案 输出割掉的边 最小割流量好求,最小割边的数量也好求,但同时确定哪条边不太好弄,因为存在方法互斥 首先:最小割流量就是跑最大流的结果 求最小割边的数量,需要在刚刚跑完最大流的网络上 把所有的满流边流量重新标记为1,不满流的重新标记为INF 在新的网络上跑一次最大流 这个时候得到的流量就是最小割边的数量 正确性: 满流边一定是某条流量通路的瓶颈路(虽然不一定是唯一瓶颈路) 把满流的边标记成1去跑增广路 得到的结果就是没有公共边的流量通路的条数(因为公共边只允许通过1点流量被计算一次) 那么就给这这些流量通路每个断开一条边即可(如果存在公共边先断开公共边) 如何求最小字典序的方案: 在最小割的情况下 首先要记住,我们一定是优先断开边权最大的必须满流边(删去这条边后,重新对整个网络跑最大流,最大流量会减小这个边的边权那么多(也就是这条边的传递作用无可替代)) 那么找最小字典序方案也出来了:在正常的图上,先跑一次最大流 然后枚举所有边(首先把边按照边权(大到小)-字典序(小到大)两个关键字排序) 先复原整个网络到未增广形态 然后尝试删去这条边,看最大流结果减少的是否是这条边流量那么多 如果是,说明这是关键边,记录这条边会被删除(贪心保证了删除的边数目最少,因为这条边满流,不删它就要删和它在同一支流的多条边) 把这条边永久性删除,并将最大流的结果减小(该边的流量)那么多 这就导致你需要先用正常的边权跑DINIC,再用1和INF的边权跑DINIC,再用正常的边权去找应当被删除的边
题目894 追查坏牛奶
AAAAAAAAAAAA
 9
评论 9
评论
2022-11-15 20:49:14
|
|
|
#include<bits/stdc++.h>
using namespace std;
int t;
int a,b,c;
int main() {
freopen("csp2022pj_pow.in","r",stdin);
freopen("csp2022pj_pow.out","w",stdout);
cin>>a>>b;
c=(pow(a,b));
if(c<0) {
cout<<-1;
} else {
cout<<c;
}
cout<<endl;
return 0;
题目3777 [CSP 2022J]乘方
AAAAAAAAAA
 3
1 条 评论 3
1 条 评论
2022-11-12 20:09:18
|
|
|
补充:这个解法是我自己的,相当麻烦,有比我简洁的 DP 做法,还有 dottle 老师的神奇最短路做法,推荐去洛谷题解看看。 首先,看到 $k\le 3$ 的范围,显然是要分类讨论。 k=1显然,最小花费即为 $u\to v$ 在树上路径的点权和。倍增预处理,每次查询 LCA 然后树上前缀和即可。 时间复杂度 $\mathcal O((n+m)\log n)$。 k=2先考虑暴力的做法。将 $u\to v$ 在树上的路径拆下来,将点权写作序列 $b_{1\sim p}$ 研究。 我们用动态规划解决这个问题。设 $f(i)$ 表示 $1\sim i$ 的最小花费。 初始状态:$f(1)=b_1$。 状态转移方程:$f(i)=\min\{f(i-1)+b_i,f(i-2)+b_i\}$。 如果对矩阵很熟悉,不难发现这个就是一个矩阵优化的板子。 不过此处 $b_i$ 是变量,无法进行矩阵快速幂,当时考场上想到这里我脑子莫名其妙宕机了,感觉这题正解绝对是矩阵,但这个东西不会处理啊,然后就彻底蒙了,完全想偏了,最后打了暴力。 实际上和快速幂没有任何关系。因为是树上的静态查询问题,自然可以往倍增想。 因为矩阵满足交换律和结合律,完全可以把矩阵先存起来预处理,最后查询的时候再一次倍增求解。 先把上面那个式子写成矩阵: $$\begin{bmatrix}f(i-1) & f(i-2)\end{bmatrix}\times\begin{bmatrix}a_i & 0\\a_i & +\infty\end{bmatrix}=\begin{bmatrix}f(i) & f(i-1)\end{bmatrix}$$ 为了方便,我们定义 $t=\text{LCA}(u,v)$,$k=3$ 时亦然。 把中间的转移矩阵存起来倍增预处理一下,询问的时候,因为正着走和倒着走没有区别,我们把 $u\to t\to v$ 拆成 $u\to t,v\to t$ 两条链,以 $u\to t$ 为例: 初始向量矩阵: $$\begin{bmatrix}a_u & +\infty \end{bmatrix}$$ 然后把 $fa_u\to t$ 上的转移矩阵全乘起来,就得到了 $u\to t$ 这条链上的答案。 类似地处理 $v\to t$,接下来考虑合并答案。 因为 $k=2$,只有两种可能:$u$ 走到 $t$ 再走到 $v$,或者不经过 $t$,直接从 $t$ 在 $u\to v$ 路径上的两个子节点处穿过。 记 $u\to t$ 的矩阵为 $P$,$v\to t$ 的矩阵为 $Q$,因为可以写作一维向量的形式,为了方便,我们直接将 $P$ 中的元素用类似序列下标的形式表示,即 $P(0),P(1)$。下面 $k=3$ 的情况里我们仍采用这种称呼。 针对两种情况,答案分别为 $P(0)+Q(0)-a_t,P(1)+Q(1)$,两者取 $\text{min}$ 即可。 时空复杂度 $\mathcal O(2^3\times (n+m)\log n)$。 k=3其实 $k=3$ 大体思路和 $k=2$ 完全一致,只不过有一个小细节:答案路径上的节点不一定都是 $u\to v$ 这条链上的。 原因很简单,比如链上的点权都是 $10^9$ 级别,而与链相连的节点中有一个点权是 1,那走这个点显然更优。 题解里大部分做法是将距离设入状态中,我当时并没有想到,而是直接把链接出去的点再设计一个方程。 还是先考虑一条链上的暴力,因为与 $u$ 相连的点中,只有点权最小的有效,设这个最小点权为 $c_u$。 在 $k=2$ 的情况上再加一条:设 $g(i)$ 表示走到 $i$ 连接的点上的最小路径花费。 状态转移方程: $$f(i)=\min\{f(i-1)+a_i,f(i-2)+a_i,f(i-3)+a_i,g(i-1)+a_i,g(i-2)+a_i\}\\g(i)=\min\{f(i-1)+c_i,f(i-2)+c_i,g(i-1)+c_i\}$$ 考虑将这个东西写成矩阵,那么样子就长这样: $$\begin{bmatrix}f(i-1) & f(i-2) & f(i-3) & g(i-1) & g(i-2)\end{bmatrix}\times \begin{bmatrix}a_i & 0 & +\infty & b_i & +\infty\\a_i & +\infty & 0 & b_i & +\infty\\a_i & +\infty & +\infty & +\infty & +\infty\\a_i & +\infty & +\infty & b_i & 0\\a_i & +\infty & +\infty & +\infty & +\infty\end{bmatrix}\\=\begin{bmatrix}f(i) & f(i-1) & f(i - 2) & g(i) & g(i-1)\end{bmatrix}$$ 倍增预处理和查询就很类似了,略过。 最后的合并情况很多,这里我直接把所有情况对应的式子列出来,因为用文字真的很难写出来 QAQ,理解一下叭 awa,有兴趣可以自己推一下,如果实在嫌我的方法麻烦还是看别的大佬的题解吧 qwq: $P(0)+Q(0)-a_t$ $P(3)+ Q(3)-c_t$ $P(1)+Q(1)$ $P(1)+Q(2)$ $P(1)+Q(4)$ $P(4)+Q(1)$ $P(2)+Q(1)$ 所有情况取 $\text{min}$ 即可。时间复杂度 $\mathcal O(5^3\times (n+m)\log n)$。
题目3784 [CSP 2022S]数据传输
AAAAAAAAAAAAAAAAAAAAAAAAA
 13
评论 13
评论
2022-11-09 19:44:30
|
|
|
zyf 的题解,写得比我好 QAQ 不难发现,答案为 YES,当且仅当所有点的出度均为 1。 考虑如何维护每个点的出度。 暴力的做法是对于每个点维护两个 set,分别表示当前与之相连/不相连的点,暴力删点加点。如果没有 $t=4$,不难发现总操作次数是 $\mathcal O(n+q)$ 级别的,可以获得 60 pts。 (据说这道题可以通过玄学暴力优化在民间数据拿到满分,毕竟这题的数据并不好造,很难有极限数据) (然而我考场上尝试玄学暴力乱搞,结果全输出 NO,爆零了 QAQ) upd:现在还没有出数据,但据说全输出 NO 能有 45 pts?乱搞选手赢麻了。 再次 upd:出数据了,我这种乱搞法居然 50pts,赢麻了,但是 rp-- 了 QAQ。 计算了一下,前 60 pts 暴力,后面全输出 NO,能有 80 pts,已经不比正解低多少了。 这道题的核心就是维护出度为 1 的点数,而有了 $t=4$ 的操作会变得非常棘手,没有任何数据结构可以维护。 一般来说(至少以窝之前打的一场 CF 看来),这种情况可以转向随机化。 考虑哈希。对每个点赋一个独一无二的权值(我采用了类似字符串哈希的构造方式),设第 $i$ 个点点权为 $a_i$,定义 $tot=\sum\limits_{i=1}^n a_i,ans=\sum\limits_{i=1}^n deg_i\times a_i$。 其中 $deg_i$ 表示点 $i$ 的出度。 由于点权都是独一无二的,若 $ans=tot$,那么就有极大的概率满足 $\forall i\in [1,n],deg_i=1$。 $tot$ 可以直接计算,而 $ans$ 的维护也相当简单,单次操作时间复杂度 $\mathcal O(1)$。 总时间复杂度为 $\mathcal O(n)$,目前在 InfOJ 上的民间数据这种方法可以拿到满分。 如果还不保险,还可以多取几个模数或点权。 upd:似乎不用我这样写,把求和改成异或,直接随机权值就完全能过了 /kel
题目3783 [CSP 2022S]星战
AAAAAAAAAAAAAAAAWWWW
 11
评论 11
评论
2022-11-08 10:56:11
|
|
|
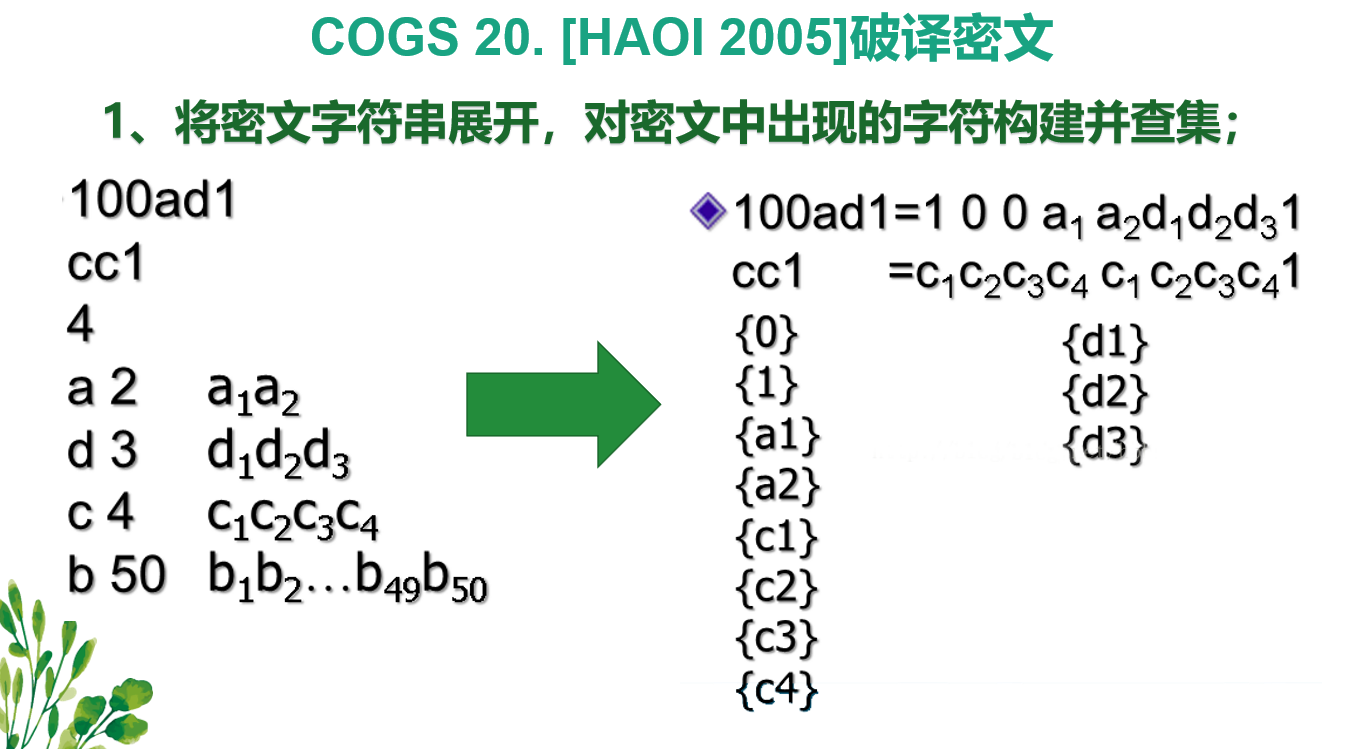
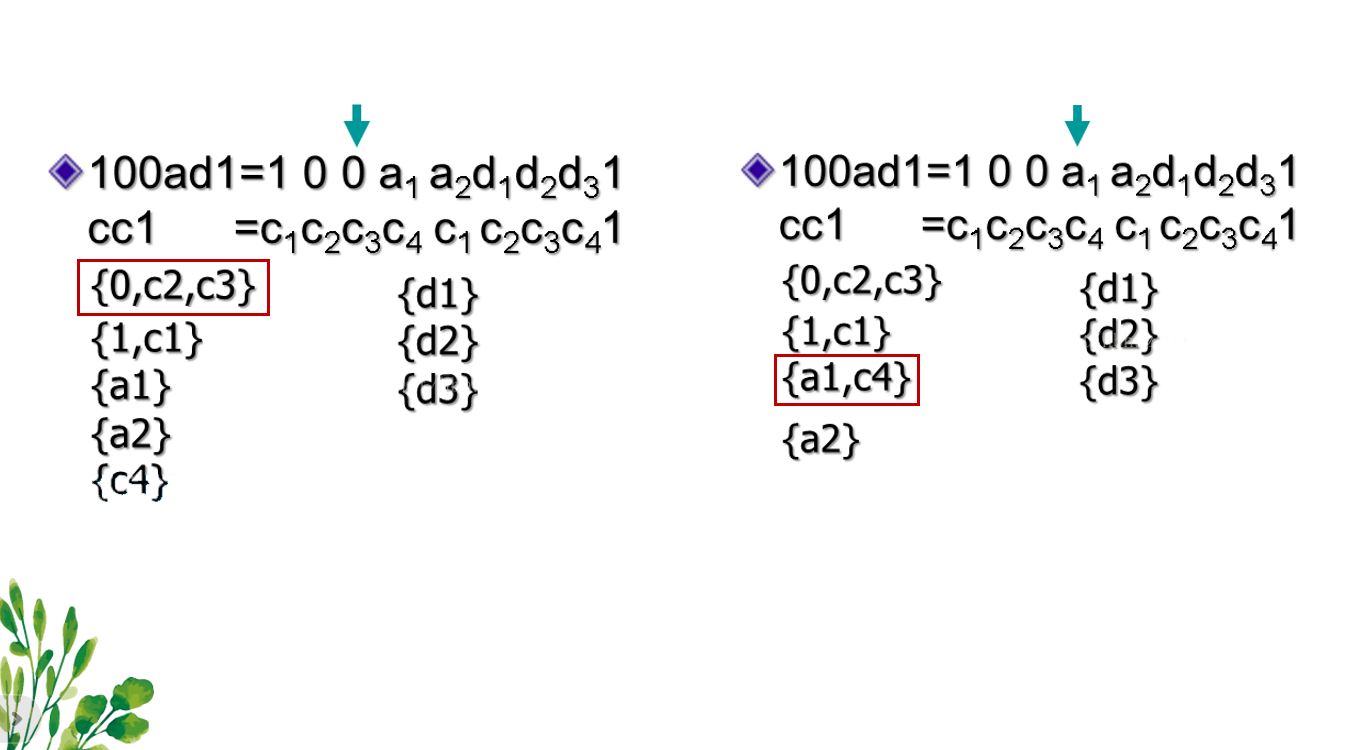
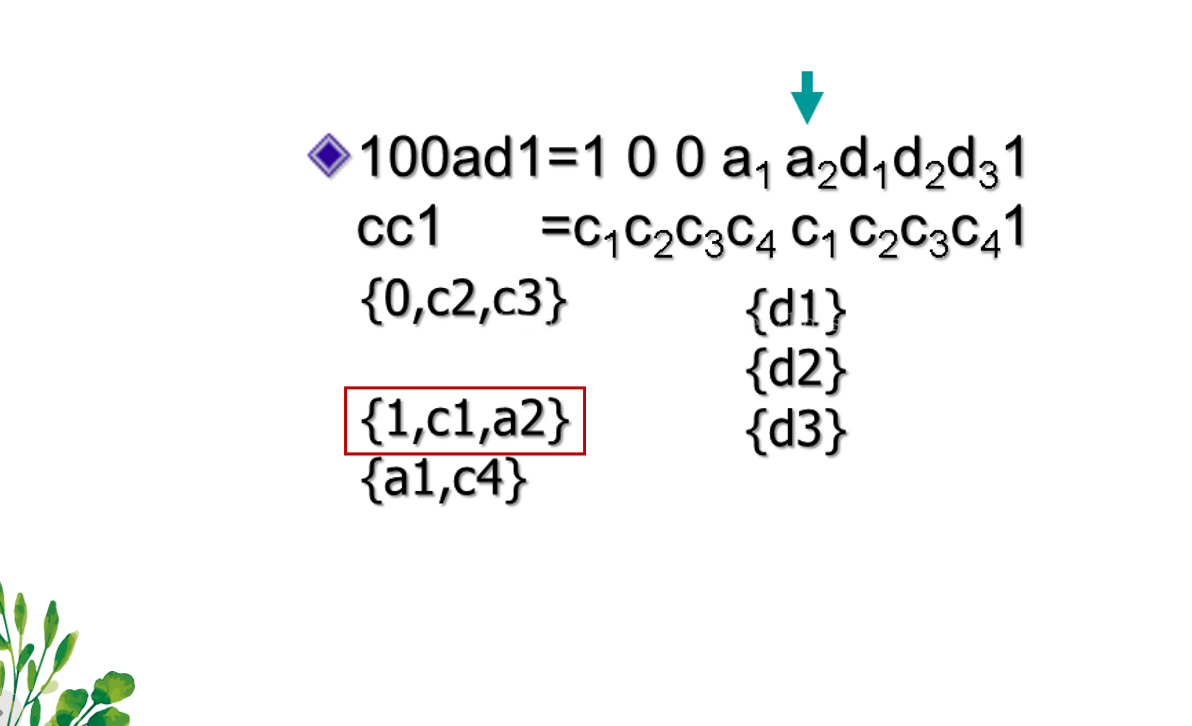
题目20 [HAOI 2005]破译密文
 7
评论 7
评论
2022-11-07 23:35:17
|
|
|
#include<bits/stdc++.h>
using namespace std;
string s1,s2;
int a[250],b[250],c[500];
int len;
int main(){
freopen("add.in","r",stdin);
freopen("add.out","w",stdout);
cin >> s1 >> s2;
for (int i = 0; i < s1.size(); i++) {
a[s1.size() - i - 1] = s1[i] - '0';
}
for (int i = 0; i < s2.size(); i++) {
b[s2.size() - i - 1] = s2[i] - '0';
}
len = s1.size();
if (s1.size() < s2.size()) {
len = s2.size();
}
for (int i = 0; i < len; i++) {
c[i] = a[i] + b[i];
}
for (int i = 0; i < len; i++) {
if (c[i] >= 10) {
c[i + 1] += c[i] / 10;
c[i] %= 10;
}
}
if (c[len] != 0) {
len++;
}
for (int i = len - 1; i >= 0; i--) {
cout << c[i];
}
}
//第一步:定义 //第二步:输入 //第三步:将字符串转换成数组 //第四步:相加(中间有进位,详见代码) //第四步:输出
题目37 增强的加法问题
AAAAAAAAAA
 3
评论 3
评论
2022-11-07 10:01:57
|