|
|
官方题解。来源:清华大学学生算法协会仓库 简要题意
区间 DP?
构造独立性
区间 DP
DP 优化
题目4262 [THUPC 2025 pre] 骑行计划
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
 1
评论 1
评论
2026-01-30 20:16:14
|
|
|
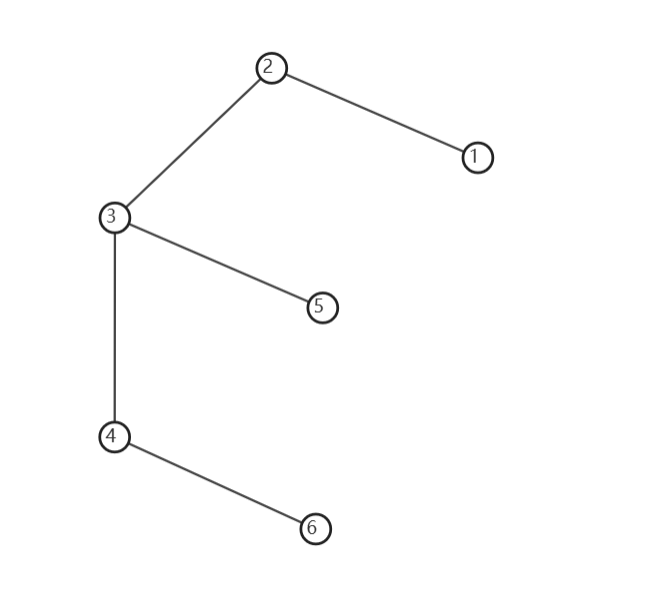
喜提最劣解(常数最大解)。第一遍甚至读错题一个小时,喜提视力最好奖。 不难发现题目要求除了给定的黑点外其他点不能染成黑色(就是读错在这里了)。 因此不难发现,若一个灰点周围有至少一个黑点,则这个点要满足两个条件之一。 一:这个点初始染成白色 二:这个点与一个初始染成白色的点相连。 然后就是很基础的东西了,因为相连在树上有儿子和父亲的关系,所以要分讨几种情况。
假如说将 $1,5,6$ 染成黑色,答案为 $1$,将 $3$ 染成白色即可,可以手玩一下,就知道怎么设置状态了。 设 $dp_{x,0/1/2/3}$ 分别表示 $x$ 不染成白色/染成白色/不染成白色,但保证父亲染成白色/不染成白色,但保证有至少一个儿子染成白色。 若 $x$ 是 $y$ 的父亲:需要保证 $dp_{y,2}$ 只能通过 $dp_{x,1}$ 转移。 对于至少一个儿子染成白色,先不强制限制,最后加上 $\min(dp_{y,1}-\min(dp_{y,0},dp_{y,1},dp_{y,3}))$ 做一个类似反悔的操作即可。 若 $x$ 初始染成黑色,则所有转移结束后令 $dp_{x,1}\gets \infty$,若 $x$ 周围至少有一个黑点,则所有转移结束后令 $dp_{x,0}\gets \infty$,防止传上去不合法的状态。 最后的答案是 $\min(dp_{1,0},dp_{1,1},dp_{1,3})$。时间复杂度为 $O(n)$。
题目4274 [THUPC 2025 pre] 辞甲猾扎
AAAAAAAAAAAA
 2
评论 2
评论
2026-01-30 19:01:12
|
|
|
感觉像是什么很复杂的博弈,应该是结论题,但是我不会猜结论。 考虑一些简单的做法,先特判掉 $n\le 3$ 的情况,因为此时一步能到达所有格子。 其他情况考虑二分答案 $mid$,判断能否得到 $\ge mid$ 的分数,这样令 $b_i=[a_i<mid]$,我们将问题转化为能否取到 $0$。 若 $b_i$ 的 $1$ 的个数 $\le 2$,因为此时 $n>3$,一定可以取到 $0$。 否则,令 $b_0=b_{n+1}=1$,若 $b_{x-1}+b_x+b_{x+1}\le 1$,则一定能取到,因为无论如何交换,第一步都能走到一个 $0$,否则则一定能控制 $b_{x-1},b_x,b_{x+1}$ 都是 $1$,必输。 然后做就行了,复杂度为 $O(Tn\log V)$。
题目4266 [THUPC 2025 pre] Harmful Machine Learning
AAAAAAAAAA
 1
评论 1
评论
2026-01-30 18:45:53
|
|
|
当 $k$ 较大时
构造答案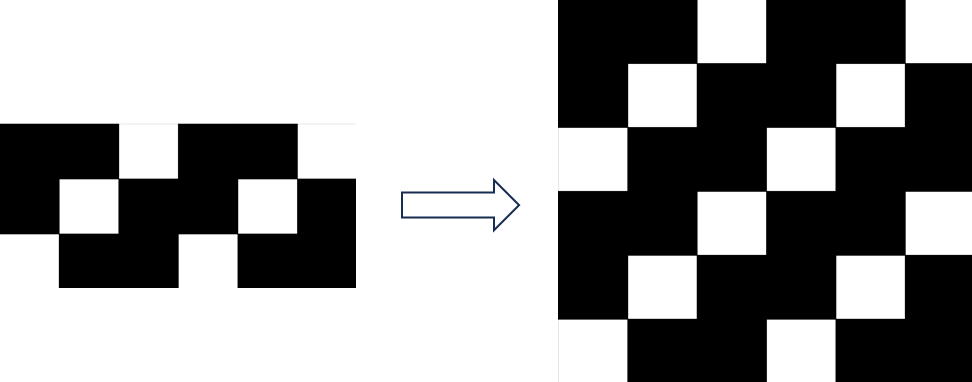
$k = \frac{2}{3}n$ 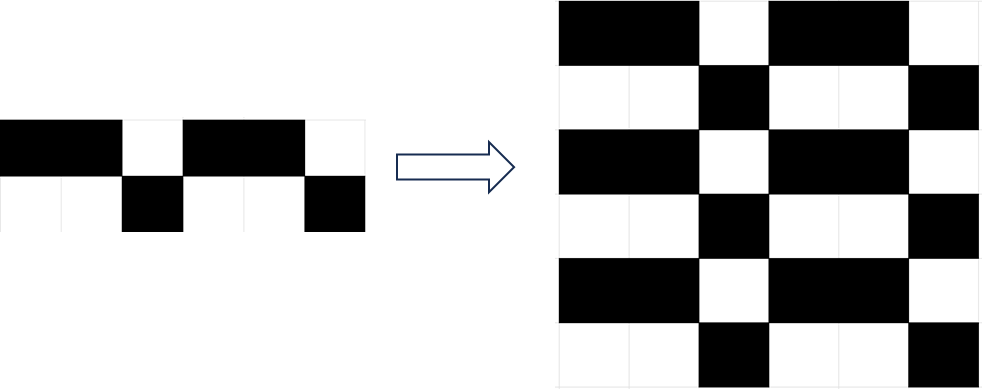
$k = \frac{1}{2}n$ 可见,它们可自由组合 $\left\lceil\frac{1}{2}n\right\rceil \le n \le \left\lfloor\frac{2}{3}n\right\rfloor$ 时均可构造。 目前的结论
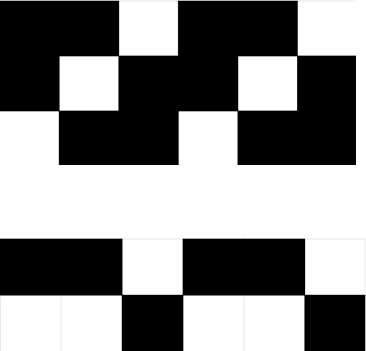
$k < \left\lceil\frac{1}{2}n\right\rceil$ 时一定有白色格三连?
$n=5, k=2$
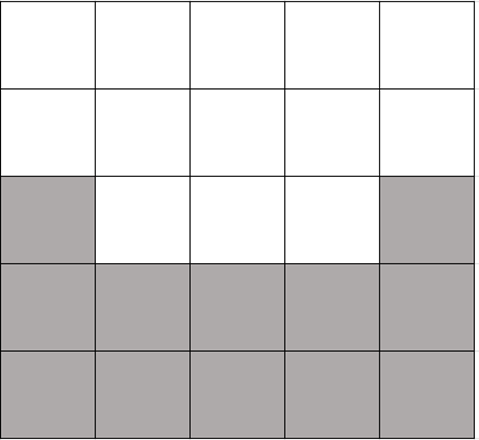
第 1, 5 列的范围是显然的; 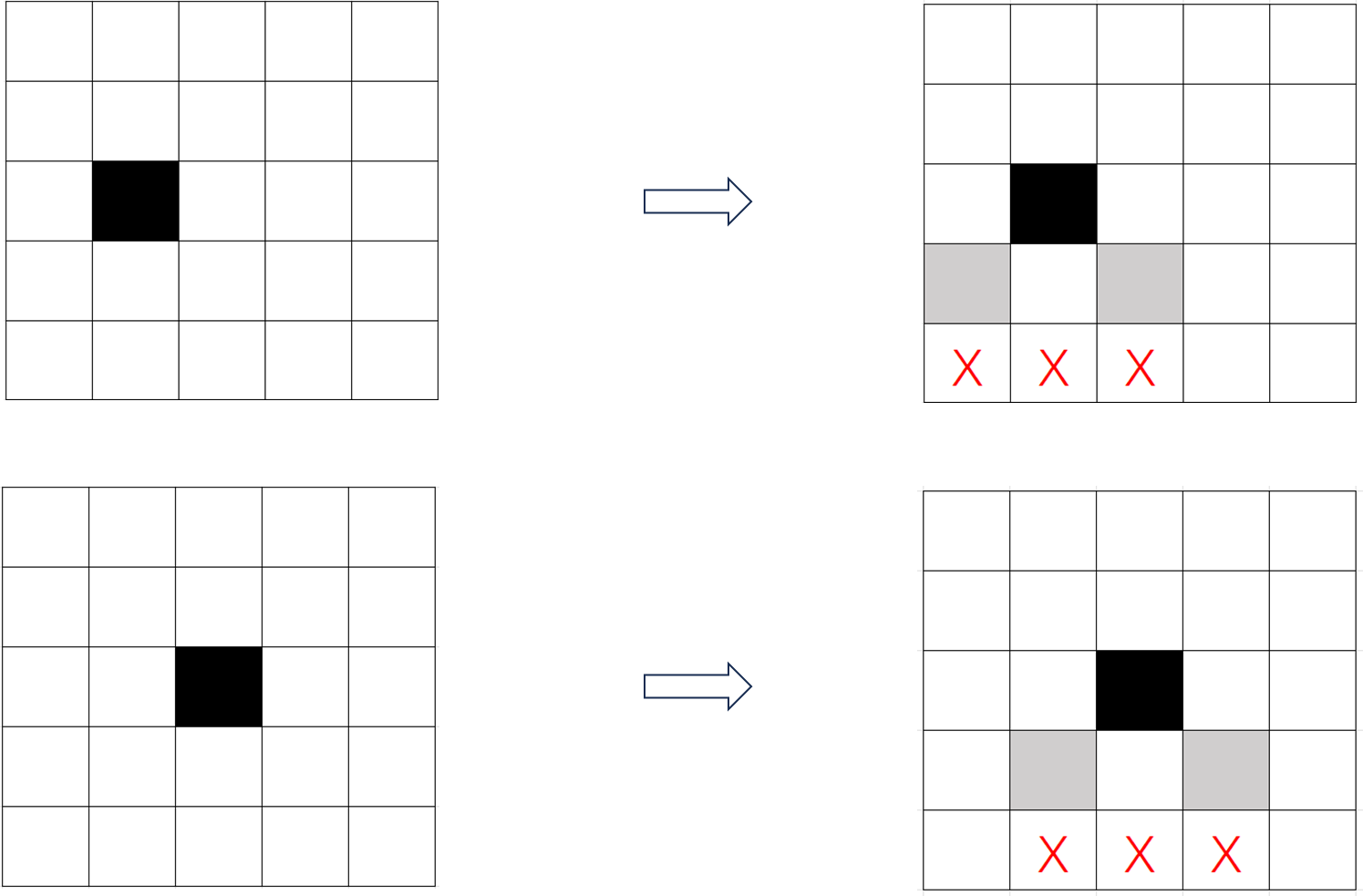
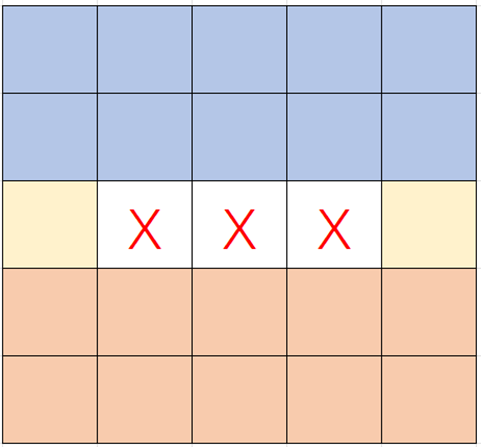
$n, k$ 更大时?($k=\lfloor\lceil\frac{1}{2}n\rfloor\rceil - 1$)
结论
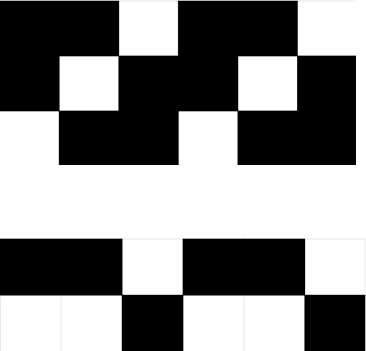
题目4285 [THUPC 2025 Final] 三元链
AAAAAAAAA
 1
评论 1
评论
2026-01-29 18:50:32
|
|
|
引言冷知识:这题曾经可能会选入今年 CTS 或者联合省选。只是因为各种各样的原因这题很早(今年一月)就没了。 其实不是一道很难的题目,思路想清楚了就非常简单了,代码也很短,最难写的地方甚至只是一个最简单情况的特判。 叫做“列队”是因为本题是因军训列队有感而出。某种意义上也是一种提示。 作为投题列表里少见的 ds 题,这题刚投就被选上了。有没有人以为这是 lxl 题? 开 5s 单纯是不想完全卡掉带 $\log$ 的做法,实际上这题只要实现优秀或者调过块长多带一点 $\log$ 都是轻松过的。 这题把大数据塞在了开头,避免卡评测太严重。 比赛情况本题预期难度是 medium+ 到 hard。不过对于熟练的 OI 选手其实应该是 medium? 来自长郡中学的队伍 Centroid.reborn(2025) 以 5 发罚时的战绩取得了首杀,似乎是写了有着巨大常数的莫队二次离线,经过各种卡常最后以 4.67s 艰难通过了。(其实没有造极限数据,认真造的话估计可以卡到 20s) 剩下的几支队伍基本都是写巨大难写的根号分治做法的。 场上甚至没看到人写正解…… 题意简述给定一个 $n \times m$ 的排列矩阵。 维护 $q$ 次操作。查询为假设反复按行列进行排序直到某次失败,最后查询单点值;修改为交换两个数。 $1 \le n \times m \le 2 \times 10^5$,$1 \le q \le 2 \times 10^5$,5s/2GB。 思路我们先证明一个引理:排序两轮后就不可能再修改了。 为什么?我们考虑把所有小于 $w$ 的数赋值为 $0$,其余赋值成 $1$,那么排序两轮后 $0$ 就会聚集在左上角而 $1$ 就会聚集在右下角。 对每个 $w$ 都如此就意味着不会再有“逆序”存在了。 于是只用分类“一次都没成功排序”和“成功排序了 $1 \sim 2$ 次”的情况。 这只用维护有多少个行内相邻的“逆序”即可判断。而这是容易做到 $O(1)$ 维护的。 第一种情况只用维护矩阵的实际形态即可解决,难点在于第二种情况。 容易发现这样问题就变成了求各行第 $y$ 小数中,第 $x$ 小的是多少。看上去就不像能 polylog 的样子。 由于限制了矩阵总大小,容易想到根号分治类算法,但是估计很难写,所以我们换个思路。 注意到这是排列,于是我们不妨考虑对每个数维护其处于的位置,然后对这个“位置数组”进行分块。 我们现在要找到一个最小的位置 $p$,使得 $p$ 之前出现过至少 $y$ 次的行号有 $x$ 种。 于是设立间断点 $0, B, 2B, \cdots$,记录间断点之前的每种行号的出现次数,以及开桶记录每个出现次数对应了多少合法(至少这么多次数)的行号。 修改操作只用修改 $O(nm/B)$ 个间断点处的信息,每次是 $O(1)$,复杂度即为 $O(nm/B)$。 而查询操作可以先通过二分或者枚举找到答案位于哪个块,再在块内不断尝试添加单项直至合法。这部分复杂度即为 $O(\log(nm/B) + B)$。 取 $B = $Θ\Theta(\sqrt{nm})$,总复杂度即可做到 $O((nm + q)\sqrt{nm})$,可以通过此题。 std 写了 2kb,没有调过块长,跑了约 700ms。 没有特意卡带 $\log$ 的做法。 总结题出的好!难度适中,覆盖知识点广,题目又着切合实际的背景,解法比较自然。给出题人点赞!
题目4289 [THUPC 2025 Final] 列队
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
 1
评论 1
评论
2026-01-29 18:41:38
|
|
|
简要题意有 $N$ 个人,$L$ 把锁和 $(L+K)$ 把钥匙。其中有 $L$ 把真钥匙,分别可以打开一把锁;另外 $K$ 把钥匙是假的,不能打开任何锁。 所有人按顺序尝试钥匙。每个人的策略都是最大化选择的钥匙打开选择的门的概率。如果有多种概率最大的组合,则等概率选择其中一种。 求打开所有锁之后每个人开锁次数的期望。 $1\le N\le 50$, $1\le L\le 5000$, $0\le K\le 50$ 求解策略为了解决这个问题,我们需要知道每个人具体会如何选择钥匙和锁。 显然,最开始的人不知道任何信息,所以只能随机选择一把钥匙和一把锁。 如果第一个人没有打开锁,第二个人有三种选法:选同一把钥匙开不同锁,选不同钥匙开同一把锁,选不同钥匙和锁。 选同一把钥匙开不同锁,或者选不同钥匙开同一把锁,解锁概率都是 $1/(L+K-1)$;选不同钥匙和锁的解锁概率是 $$\frac{1 - \frac{1}{L+K-1}}{L+K-1} = \frac{L+K-2}{(L+K-1)^2} < \frac{1}{L+K-1}$$ 所以第二个人会以 $(L-1)/(2L+K-2)$ 的概率选同一把钥匙开不同锁,以 $(L+K-1)/(2L+K-2)$ 概率选不同钥匙开同一把锁。 结论同理可以继续分析后续各人的策略。结论为:如果第二个人选择了同一把钥匙,则接下来每个人都会选择这把钥匙;如果第二个人选择了同一把锁,则接下来每个人都会选择这把锁。 不难想到记录 $f_i(l, k)$ 表示 $L=l, K=k$ 时第 $i$ 个人的期望开锁次数,则可以对 $f$ 进行 DP。 另一种做法是,记 $p_i(l, k)$ 表示已经打开了 $l$ 把锁,发现 $k$ 把假钥匙,轮到第 $i$ 个人进行首次尝试的概率(此时除了 $l$ 和 $k$ 以外没有任何额外信息,重置到所有组合等概率的状态),另外记 $E_i$ 表示答案。 出题人写的是后一种写法,验题人写的是前一种写法,都可以通过。 转移因为决策有三类,所以转移分为三种:第一个人直接开锁,第二个人开锁(分相同钥匙还是相同锁讨论),后续其余人开锁(同样分类讨论)。 前两种转移都是 $O(1)$ 的,第三种转移如果直接做是 $O(L+K)$ 的,总复杂度 $O(NLK\cdot (L+K))$,不能通过本题。 推式子可知,对于第三种转移而言,恰是某一次尝试时解锁的概率是相等的。直观理解:多人抓阄,是每个人按顺序抓并直接打开,还是所有人先抓完再一起打开,并不影响每个人抽中的概率。 由此可知,我们只需要统计每个第三种转移中,每个人可以尝试多少次,再乘上相应的概率即可。这样可以将复杂度降低到 $O(NLK\cdot N)$,但仍然不能通过。
进一步优化冷静分析:因为尝试是按顺序进行的,所以尝试的次数很平均。
因为相同尝试次数(也即相同转移系数)的极长连续段只有 $O(1)$ 个,所以可以用前缀和的方式,将第三种转移优化到 $O(1)$。总复杂度 $O(NLK)$,可以通过本题。
题目4288 [THUPC 2025 Final] 喜爱之钥
AAAAAAAAAAAAAAAAAAAA
 1
评论 1
评论
2026-01-29 18:41:20
|