|
|
先吐槽下COGS评测机,洛谷AC,这里不开O2会T( 以下转载于我的洛谷博客:
赛场切了很开心,于是写篇题解。
看到题后我们可以想一下,每次两人可能进行的操作会是什么。
如果第一个人选了正数,第二个人首先会选最小的负数(前提是能选到负数),没有负数第二个人会选 $0$,没有 $0$ 就会选最小的正数。
如果第一个人选了负数,第二个人会选最大的正数,没有正数第二个人会选 $0$,没有 $0$ 会选最小的负数。
如果第一个人选 $0$,第二个人无论怎么选,答案都是 $0$。
那么,我们就可以让第一个人根据第二个人有的数字来确定自己选什么。
分情况讨论,如果第一个人有 $0$,先让答案等于 $0$。
如果第一个人有正数,结合上面的分析,可以得出,答案可能是第一个人的最小正数乘以第二个人的最大负数、第一个人的最大正数乘以第二个人的最小正数、$0$。
负数同理,可能是第一个人的最大负数乘以第二个人的最大正数、第一个人的最小负数乘以第二个人的最大负数、$0$。
那么这个题目就转化为求两个区间的最大正数、最小正数、最大负数、最小负数和是否有 $0$。
最常见的方法是写个线段树,但是由于我线段树太烂~~以及很喜欢分块~~,我最后写了分块。后来我发现,线段树的做法其实比分块要简单太多,我写的分块的码量几乎是别人线段树的两倍。
另外,我发现我打的分块求是否有 $0$ 出了很多奇怪的错误,于是求是否有 $0$ 我使用了前缀和。
以下是带注释的代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN = 100010;
int n, m, q, s, a[MAXN], b[MAXN];
int maxn1a[500], maxn2a[500], minn1a[500], minn2a[500], is0a[MAXN]; // 分块,对应序列 a
int maxn1b[500], maxn2b[500], minn1b[500], minn2b[500], is0b[MAXN]; // 序列 b
struct node {
int maxn1, maxn2, minn1, minn2, is0;
}; // 分别对应最大的正数、最大的负数、最小的正数、最小的负数、是否有 0
node query1(int x, int y) { // 处理序列 a
int ka = x / s, kb = y / s;
node ans;
ans.maxn2 = -0x3f3f3f3f3f3f3f3f;
ans.minn1 = 0x3f3f3f3f3f3f3f3f;
ans.maxn1 = 0;
ans.minn2 = 0;
if(ka == kb) {
for(int i = x; i <= y; i ++) {
if(a[i] < 0) {
ans.maxn2 = max(ans.maxn2, a[i]);
ans.minn2 = min(ans.minn2, a[i]);
}
if(a[i] > 0) {
ans.maxn1 = max(ans.maxn1, a[i]);
ans.minn1 = min(ans.minn1, a[i]);
}
}
return ans;
}
for(int i = x; i < (ka + 1) * s; i ++) {
if(a[i] < 0) {
ans.maxn2 = max(ans.maxn2, a[i]);
ans.minn2 = min(ans.minn2, a[i]);
}
if(a[i] > 0) {
ans.maxn1 = max(ans.maxn1, a[i]);
ans.minn1 = min(ans.minn1, a[i]);
}
}
for(int i = kb * s; i <= y; i ++) {
if(a[i] < 0) {
ans.maxn2 = max(ans.maxn2, a[i]);
ans.minn2 = min(ans.minn2, a[i]);
}
if(a[i] > 0) {
ans.maxn1 = max(ans.maxn1, a[i]);
ans.minn1 = min(ans.minn1, a[i]);
}
}
for(int i = ka + 1; i < kb; i ++) {
ans.maxn2 = max(ans.maxn2, maxn2a[i]);
ans.minn2 = min(ans.minn2, minn2a[i]);
ans.maxn1 = max(ans.maxn1, maxn1a[i]);
ans.minn1 = min(ans.minn1, minn1a[i]);
}
return ans;
}
node query2(int x, int y) { // 序列 b
int ka = x / s, kb = y / s;
node ans;
ans.maxn2 = -0x3f3f3f3f3f3f3f3f;
ans.minn1 = 0x3f3f3f3f3f3f3f3f;
ans.maxn1 = 0;
ans.minn2 = 0;
if(ka == kb) {
for(int i = x; i <= y; i ++) {
if(b[i] < 0) {
ans.maxn2 = max(ans.maxn2, b[i]);
ans.minn2 = min(ans.minn2, b[i]);
}
if(b[i] > 0) {
ans.maxn1 = max(ans.maxn1, b[i]);
ans.minn1 = min(ans.minn1, b[i]);
}
}
return ans;
}
for(int i = x; i < (ka + 1) * s; i ++) {
if(b[i] < 0) {
ans.maxn2 = max(ans.maxn2, b[i]);
ans.minn2 = min(ans.minn2, b[i]);
}
if(b[i] > 0) {
ans.maxn1 = max(ans.maxn1, b[i]);
ans.minn1 = min(ans.minn1, b[i]);
}
}
for(int i = kb * s; i <= y; i ++) {
if(b[i] < 0) {
ans.maxn2 = max(ans.maxn2, b[i]);
ans.minn2 = min(ans.minn2, b[i]);
}
if(b[i] > 0) {
ans.maxn1 = max(ans.maxn1, b[i]);
ans.minn1 = min(ans.minn1, b[i]);
}
}
for(int i = ka + 1; i < kb; i ++) {
ans.maxn2 = max(ans.maxn2, maxn2b[i]);
ans.minn2 = min(ans.minn2, minn2b[i]);
ans.maxn1 = max(ans.maxn1, maxn1b[i]);
ans.minn1 = min(ans.minn1, minn1b[i]);
}
return ans;
}
signed main() {
cin >> n >> m >> q;
s = sqrt(n);
memset(maxn2a, -0x3f, sizeof(maxn2a));
memset(minn1a, 0x3f, sizeof(minn1a));
memset(maxn2b, -0x3f, sizeof(maxn2b));
memset(minn1b, 0x3f, sizeof(minn1b));
for(int i = 1; i <= n; i ++) {
cin >> a[i];
is0a[i] = is0a[i - 1]; // 前缀和处理是否有 0
if(a[i] == 0) {
is0a[i] ++;
}
if(a[i] < 0) {
maxn2a[i / s] = max(maxn2a[i / s], a[i]); // 处理每一块的最大最小值
minn2a[i / s] = min(minn2a[i / s], a[i]);
}
if(a[i] > 0) {
maxn1a[i / s] = max(maxn1a[i / s], a[i]);
minn1a[i / s] = min(minn1a[i / s], a[i]);
}
}
for(int i = 1; i <= m; i ++) {
cin >> b[i];
is0b[i] = is0b[i - 1];
if(b[i] == 0) {
is0b[i] ++;
}
if(b[i] < 0) {
maxn2b[i / s] = max(maxn2b[i / s], b[i]); // 同上
minn2b[i / s] = min(minn2b[i / s], b[i]);
}
if(b[i] > 0) {
maxn1b[i / s] = max(maxn1b[i / s], b[i]);
minn1b[i / s] = min(minn1b[i / s], b[i]);
}
}
for(int i = 1; i <= q; i ++) {
int l1, l2, r1, r2, ans = -0x3f3f3f3f3f3f3f3f;
cin >> l1 >> r1 >> l2 >> r2;
node ans1 = query1(l1, r1);
ans1.is0 = is0a[r1] - is0a[l1 - 1];
node ans2 = query2(l2, r2);
ans2.is0 = is0b[r2] - is0b[l2 - 1]; // 分别求两个区间
if(ans1.is0) {
ans = 0; // 特判序列 a中有 0
}
if(ans1.maxn1) { // 分析中的各种情况分别处理
if(ans2.minn2) {
ans = max(ans, ans1.minn1 * ans2.minn2);
}
else if(ans2.is0) {
ans = max(ans, (int)0);
}
else {
ans = max(ans, ans1.maxn1 * ans2.minn1);
}
}
if(ans1.minn2) {
if(ans2.maxn1) {
ans = max(ans, ans1.maxn2 * ans2.maxn1);
}
else if(ans2.is0) {
ans = max(ans, (int)0);
}
else {
ans = max(ans, ans1.minn2 * ans2.maxn2);
}
}
cout << ans << endl;
}
return 0;
}
题目3782 [CSP 2022S]策略游戏
AAAAAAAAAAAAAAAAAAAA
 10
评论 10
评论
2022-11-06 13:47:26
|
|
|
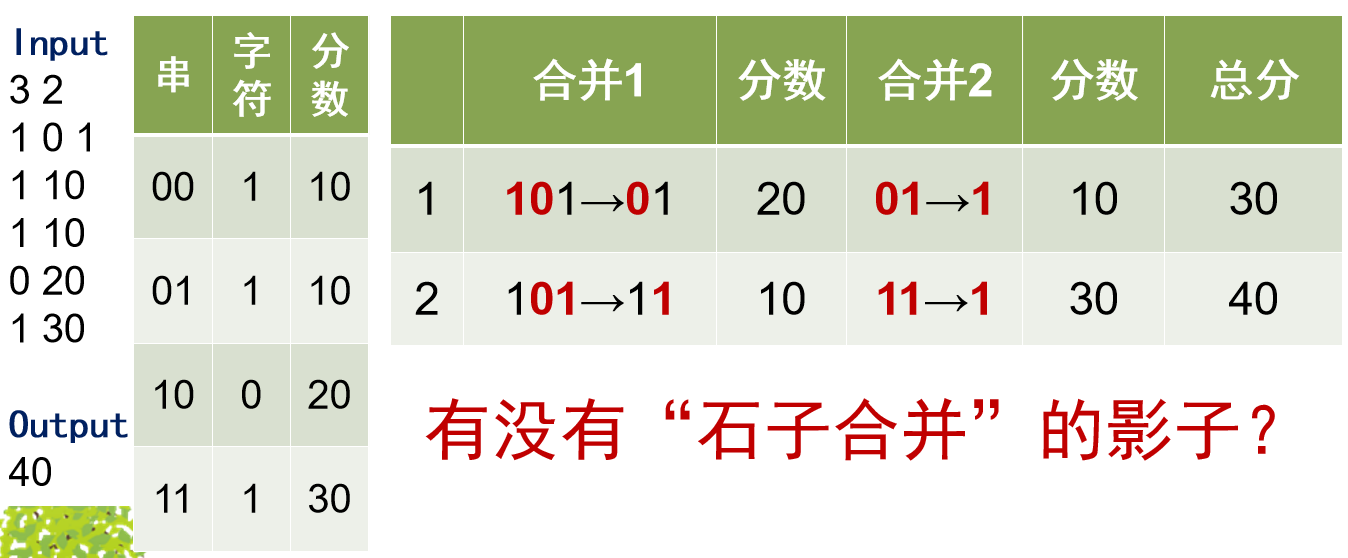
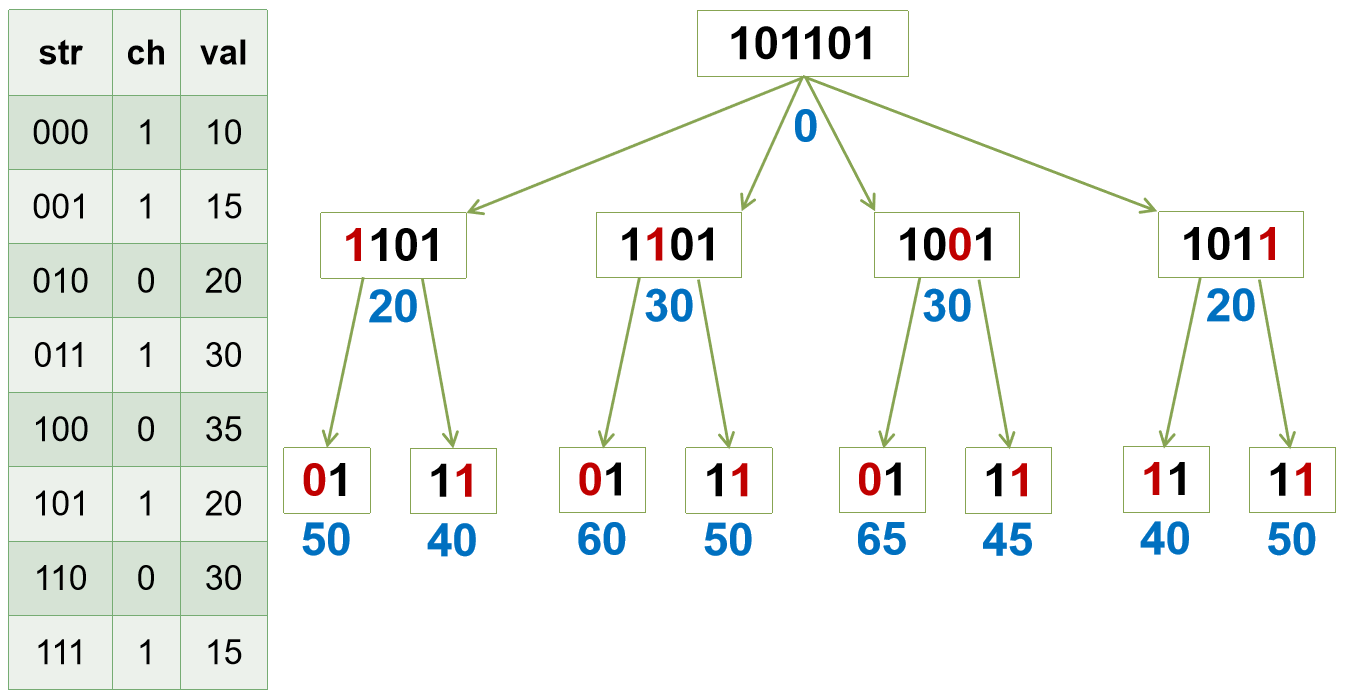
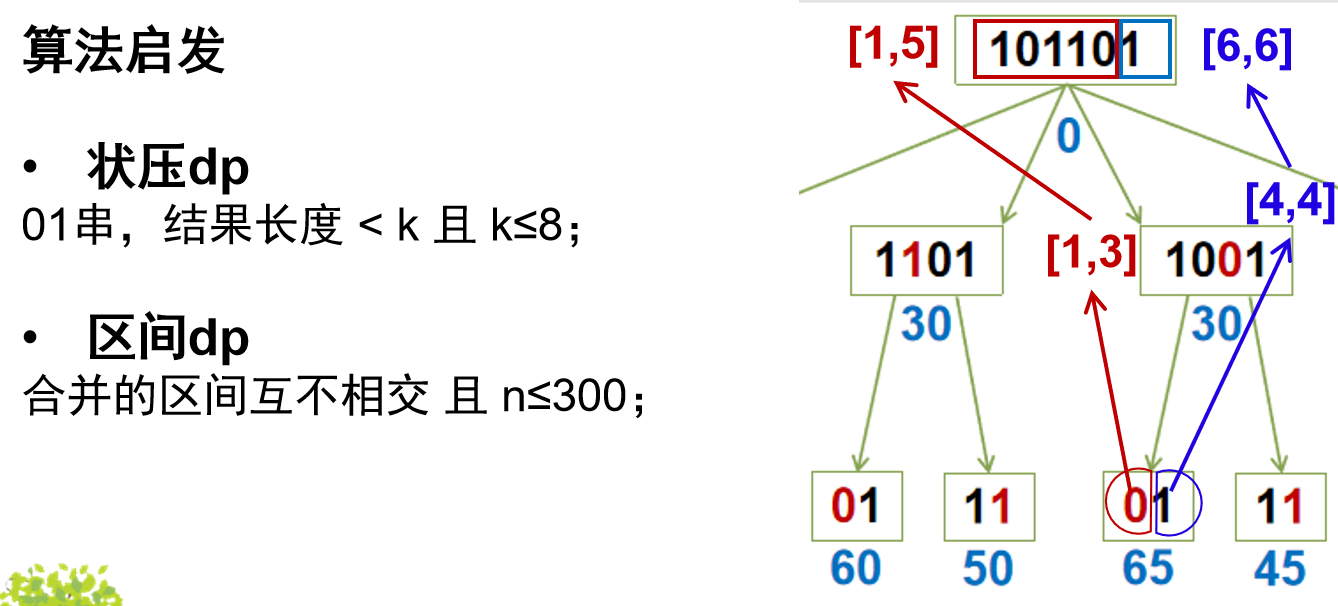
题目2269 [HAOI 2016]字符合并
 7
评论 7
评论
2022-11-05 20:42:23
|
|
|
这题我在考试的时候是100,为什么在这只有40 这题不难,但是容易陷入思维陷阱中。就是说,c++中的<cmath>头文件有直接算出乘方的 pow 函数,但是很明显在这里不能直接用。这里的结果很可能会超过10^18,就会输出乱码。因此我们可以定义一个函数panduan,返回值是long long(结果小于等于10^9),里面是a和b,也是long long.代码如下:
#define ll long long
ll panduan(ll a,ll b){
ll ans=1;
for(ll i=1;i<=b;i++){
ans=ans*a;
if(ans>1000000000) return -1;
}
return ans;
}
然后就可以了,完整代码交给读者自行锻炼
题目3777 [CSP 2022J]乘方
 2
1 条 评论 2
1 条 评论
2022-11-04 11:34:42
|
|
|
有两种方法:一种是先求最小生成树,然后删边;另一种是先把除了节点一以外的连通块分别求出来最小生成树,将每个连通块和节点一连边,然后不断更新答案。 第一种方法的时间复杂度为 $O(n^4)$,第二种方法的时间复杂度为 $O(n^2)$。
解法一 代码 解法二 代码
题目3463 [POJ 1639]野餐计划
 6
评论 6
评论
2022-11-02 23:39:25
|
|
|
(出题人 $Brian Dean$ 题解 $yuan$译)
此问题是一种递归(深度优先)搜索以识别图形中的连接组件的练习。 第一项任务比第二项任务简单得多。我们建一个图,其中每个单元格是一个结点,如果它们包含相同的数字,则两个相邻的单元格连接一条边。 然后,我们从每个单元格开始递归 $Flood$ 填充(跳过已经访问过的单元格),扩展每个联通区域,并累加联通区域的大小。
对于第二项任务,我们为每对奶牛$(x,y)$创建一个图,结点是我们在第一个任务中计算的区域,用一条边连接相邻区域, 其中一个区域用 $x$ 标记,另一个区域用 $y$ 标记。 图中的每个结点被赋予一个“权”值,其权值与第一个任务的相应区域的大小相同,然后我们在每个图形上开始递归 $Flood$ 填充以找到具有最大面积的任何一个。
这里有两个重要的想法可以使我们的解决方案快速运行。 一是确保第一个任务中的每个区域在第二个任务中都被压缩为单个结点。 如果我们不这样做,那么在第二个任务中,我们可能会反复递归扫描同一大片区域,浪费大量时间。 另一个方法是,当我们进行递归搜索时,我们需要确保运行时间仅依赖于图中的边数而不是结点数,因为第二个任务图中涉及大量结点,但可能边数很少。 例如,我们不希望为每个结点保留一个“是否遍历过”的标记数组,并且在每个递归搜索时都被初始化为 $false$。 相反,在下面的解决方案中,我们为此使用了映射数据结构,它只在需要时创建标志,避免初始化不相关结点的初始化标志。
每个数字块是一个整体,用并查集维护大小 ; 给所有相邻数字块建边 ,并根据颜色排序 ; 处理每个数字块与哪些数字块相连,维护一个颜色连接着哪些数字块; 枚举处理所有相邻的数字块方案,已经根据数字值排在一起;
$Brian$ $Dean$ 的代码如下: #include <iostream>
#include <fstream>
#include <map>
#include <set>
#include <algorithm>
using namespace std;
int N, B[1001][1001], cellid[1001][1001], global_regid;
struct Graph {
map<int,set<int>> out_edges;
map<int,int> nodesize, regid; // size of each node and region ID to which it belongs
map<int,int> regsize; // size of each region
};
typedef pair<int,int> pii;
map<int, Graph> G1; // Graphs for all possible single IDs
map<pii, Graph> G2; // Graphs for all possible adjacent region pairs
// Return size of region reachable from nodeid
int visit(Graph &G, int nodeid, int regid)
{
if (G.regid.count(nodeid) > 0) return 0; // already visited? bail out
G.regid[nodeid] = regid; // mark this node as visited
int a = G.nodesize[nodeid]; // tally up region size
for (int nbrid : G.out_edges[nodeid])
a += visit(G, nbrid, regid);
G.regsize[regid] = a;
return a;
}
// Compute region sizes and return largest region size in graph.
// Running time only depends on # of edges, not # of nodes, so graph can be very sparse
int largest_region(Graph &G)
{
int m = 0;
for (auto &p : G.out_edges) m = max(m, visit(G, p.first, ++global_regid));
return m;
}
void add_edge(Graph &G, int node1, int node2)
{
G.out_edges[node1].insert(node2);
G.out_edges[node2].insert(node1);
G.nodesize[node1] = G.nodesize[node2] = 1;
}
// Add edge between two regions in a region pair graph
void add_G2_edge(int i1, int j1, int i2, int j2)
{
int b1 = B[i1][j1], b2 = B[i2][j2], c1 = cellid[i1][j1], c2 = cellid[i2][j2];
if (b1 > b2) { swap (b1,b2); swap(c1,c2); }
int r1 = G1[b1].regid[c1], r2 = G1[b2].regid[c2];
pii p = make_pair(b1, b2);
add_edge(G2[p], r1, r2);
G2[p].nodesize[r1] = G1[b1].regsize[r1];
G2[p].nodesize[r2] = G1[b2].regsize[r2];
}
int main()
{
ifstream fin ("multimoo.in");
ofstream fout ("multimoo.out");
fin >> N;
for (int i=1; i<=N; i++)
for (int j=1; j<=N; j++) {
fin >> B[i][j];
cellid[i][j] = i*N+j; // unique ID for each cell
}
// Build primary graph
for (int i=1; i<=N; i++)
for (int j=1; j<=N; j++) {
add_edge(G1[B[i][j]],cellid[i][j],cellid[i][j]);
if (i<N && B[i+1][j] == B[i][j]) add_edge(G1[B[i][j]], cellid[i][j], cellid[i+1][j]);
if (j<N && B[i][j+1] == B[i][j]) add_edge(G1[B[i][j]], cellid[i][j], cellid[i][j+1]);
}
// Find largest region in primary graph
int answer1 = 0;
for (auto &p : G1) answer1 = max(answer1,largest_region(p.second));
// Build secondary graphs based on regions of the primary graph that are adjacent
for (int i=1; i<=N; i++)
for (int j=1; j<=N; j++) {
if (i<N && B[i+1][j] != B[i][j]) add_G2_edge(i,j,i+1,j);
if (j<N && B[i][j+1] != B[i][j]) add_G2_edge(i,j,i,j+1);
}
// Find largest region in secondary graphs
int answer2 = 0;
for (auto &p : G2) answer2 = max(answer2, largest_region(p.second));
fout << answer1 << "\n";
fout << answer2 << "\n";
return 0;
}
题目3045 [USACO Open18 Silver] Multiplayer Moo
AAAAAAAAAA
 7
评论 7
评论
2022-11-02 20:22:34
|
|
|
因为边最多有 $100$ 条,所以有效的节点编号最多只有 $200$ 个,考虑离散化。 设离散化之后的 $P \times P$ 的邻接矩阵 $A$ ,那么不难想到这个邻接矩阵经过两条边的最短路就是 $\displaystyle B[i, j] = \min_{1 \le k \le P} {A[i, k] + A[k, j]} \notag $ 紧接着,经过三条边的最短路也不难想到。 $\displaystyle C[i, j] = \min_{1 \le k \le P} {A[i, k] + B[k, j]} \notag $ 联想到什么了吗?像乘法一样!实际上,求经过 $n$ 条边的最短路等价于一个广义“矩阵乘法”,用 $A^m$ 表示经过 $m$ 条边的最短路的话,就能表示出来一般的式子: $\displaystyle A^{a + b}[i, j] = \min_{1 \le k \le P} {A^a[i, k] + A^b[k, j]} \notag $ 于是,求几条边就相当于求“几次幂”,求幂的话当然是快速幂了。 具体到这个广义的“矩阵乘法”快速幂的话,一次“矩阵乘法”就类似于进行一次 $\mathrm{floyd}$。
题目1470 [USACO Nov07] 奶牛接力
AAAAAAAAAA
 7
评论 7
评论
2022-10-31 22:09:30
|