|
|
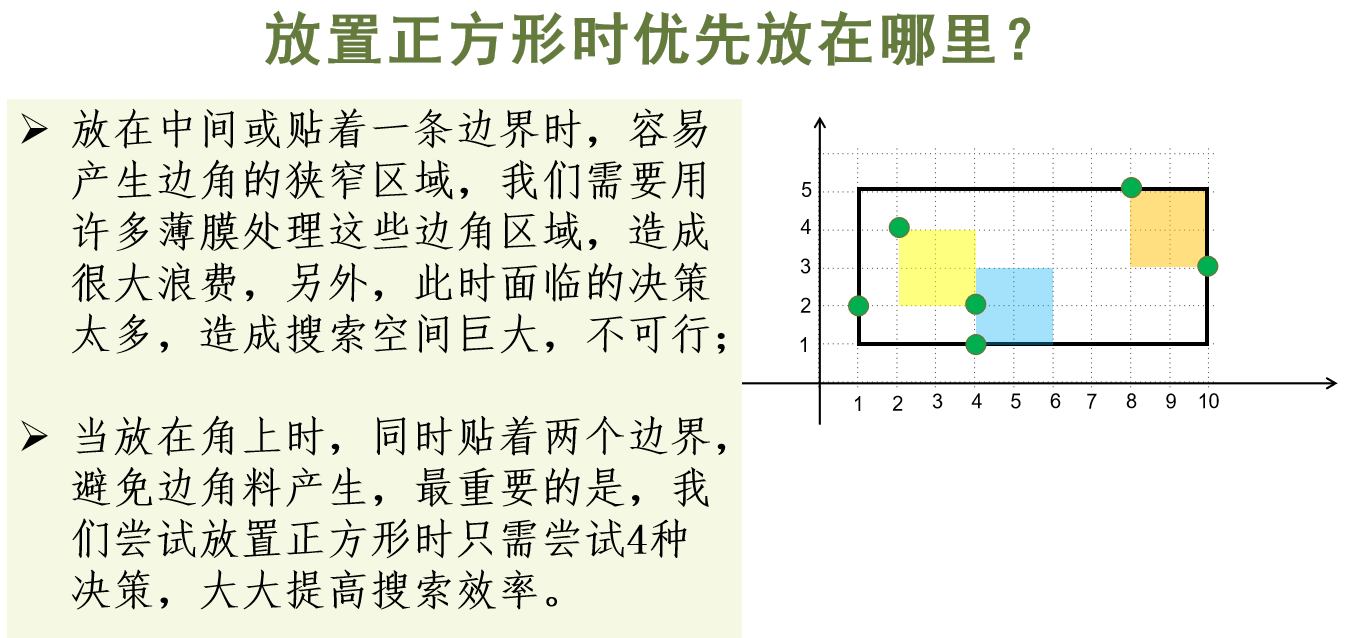
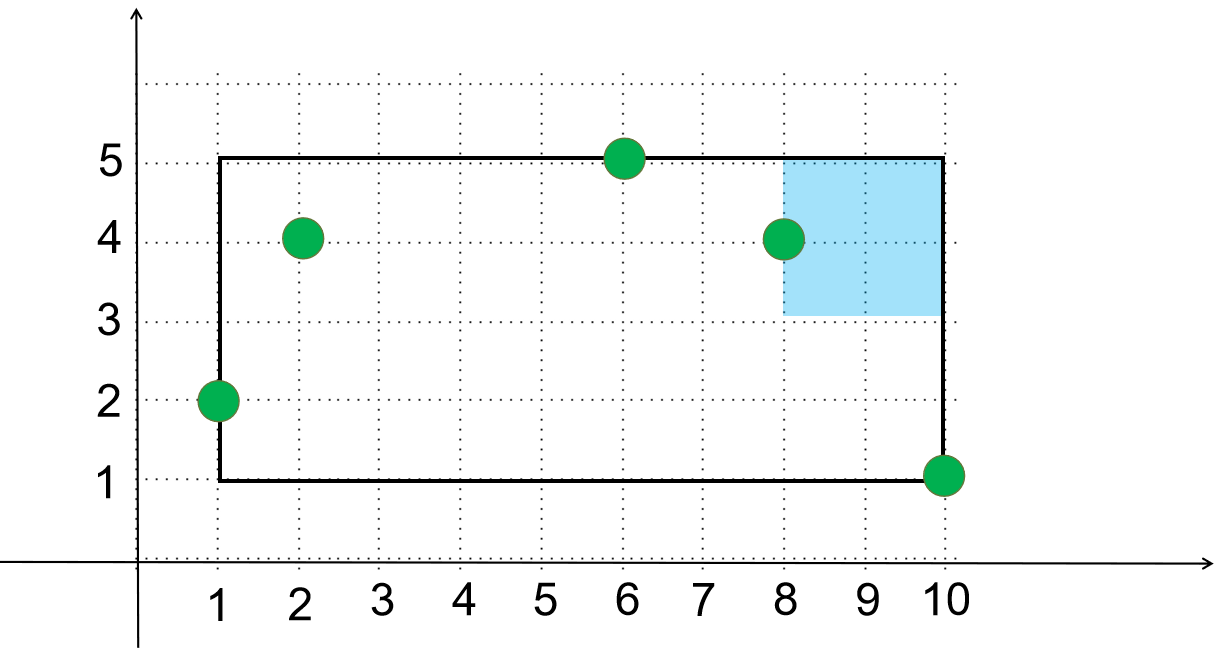
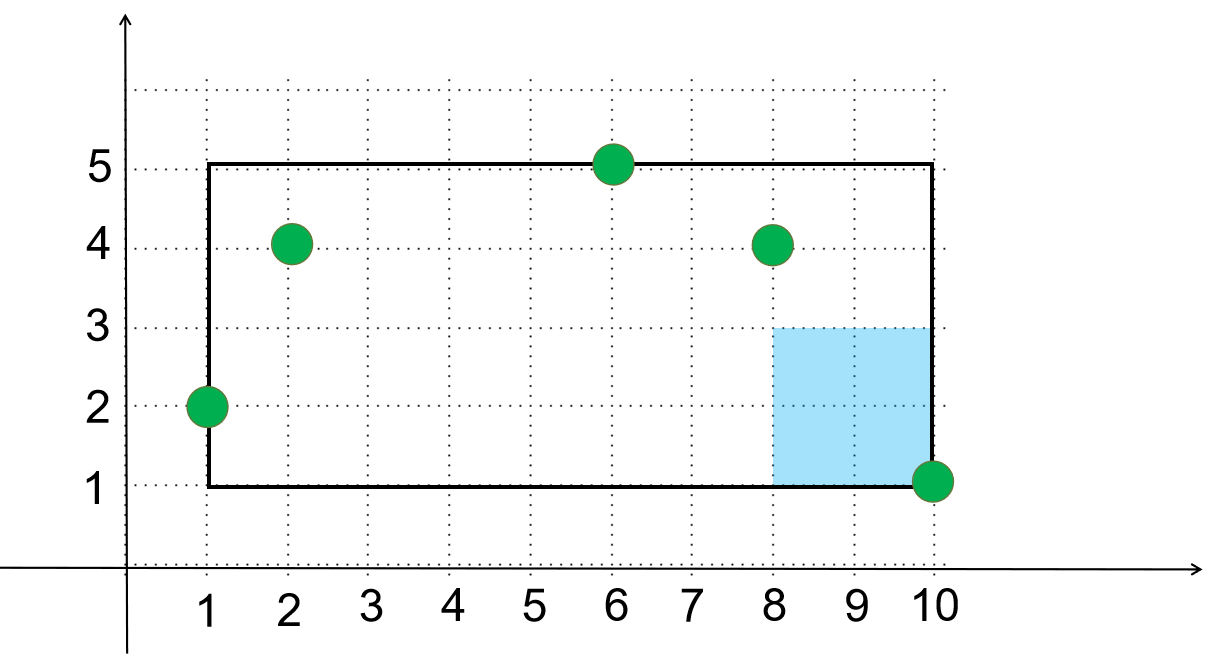
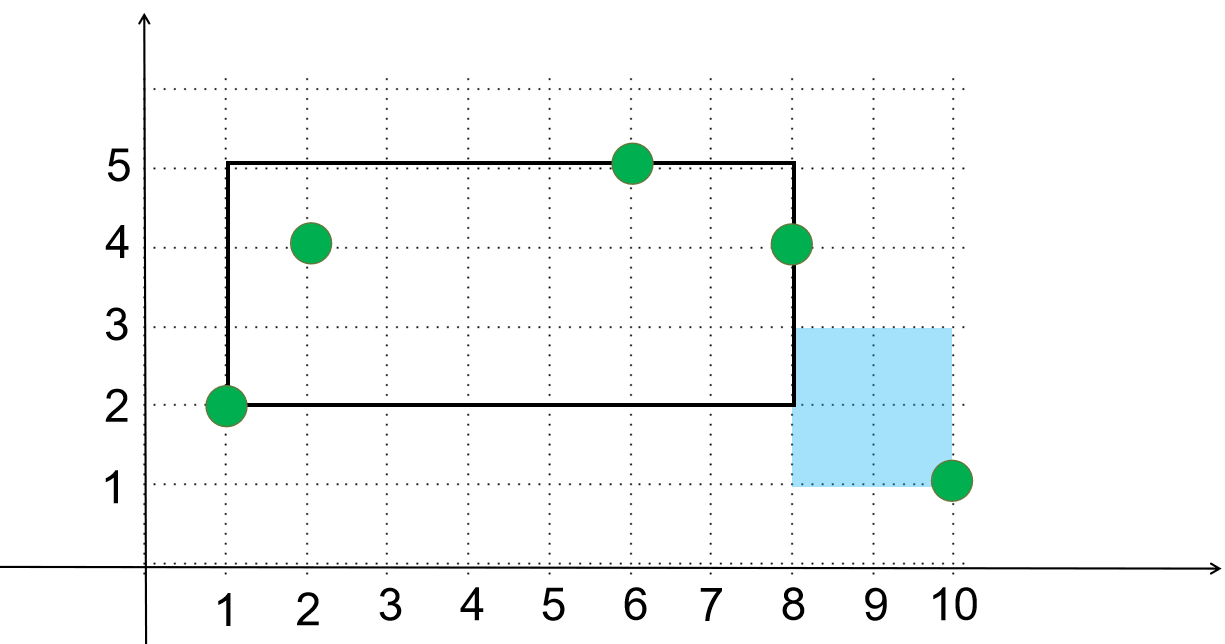
题目1312 [HAOI 2007]覆盖问题
 8
评论 8
评论
2022-10-30 22:56:53
|
|
|
这题实际上相当于在一条 $1$ ~ $n$ 的路径,找到两个点 $a, b$(先经过 $a$),使得 $w(b) - w(a)$ 最大。 可以用 SPFA 算法维护从节点 $1$ 到其它节点的点权值的最小值,以及节点 $n$ 到该节点的点权值的最大值,具体实现时候,用 $\min(min(u), w(v))$ 代替 $min(u) + w(v)$ 进行松弛就可以了。 最后枚举所有的节点,找到 $\displaystyle \max_{1 \le i \le n}(max(i) - min(i))$ 。
题目406 [NOIP 2009]最优贸易
AAAAAAAAAA
 7
评论 7
评论
2022-10-27 15:06:15
|
|
|
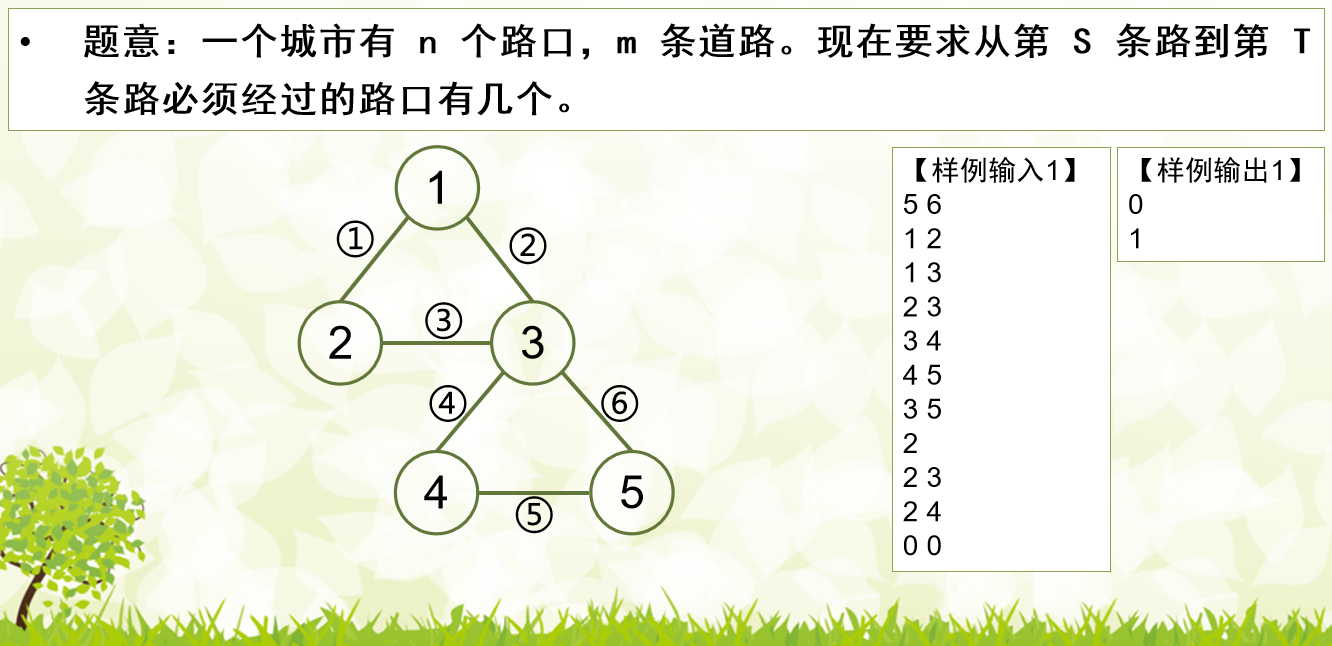
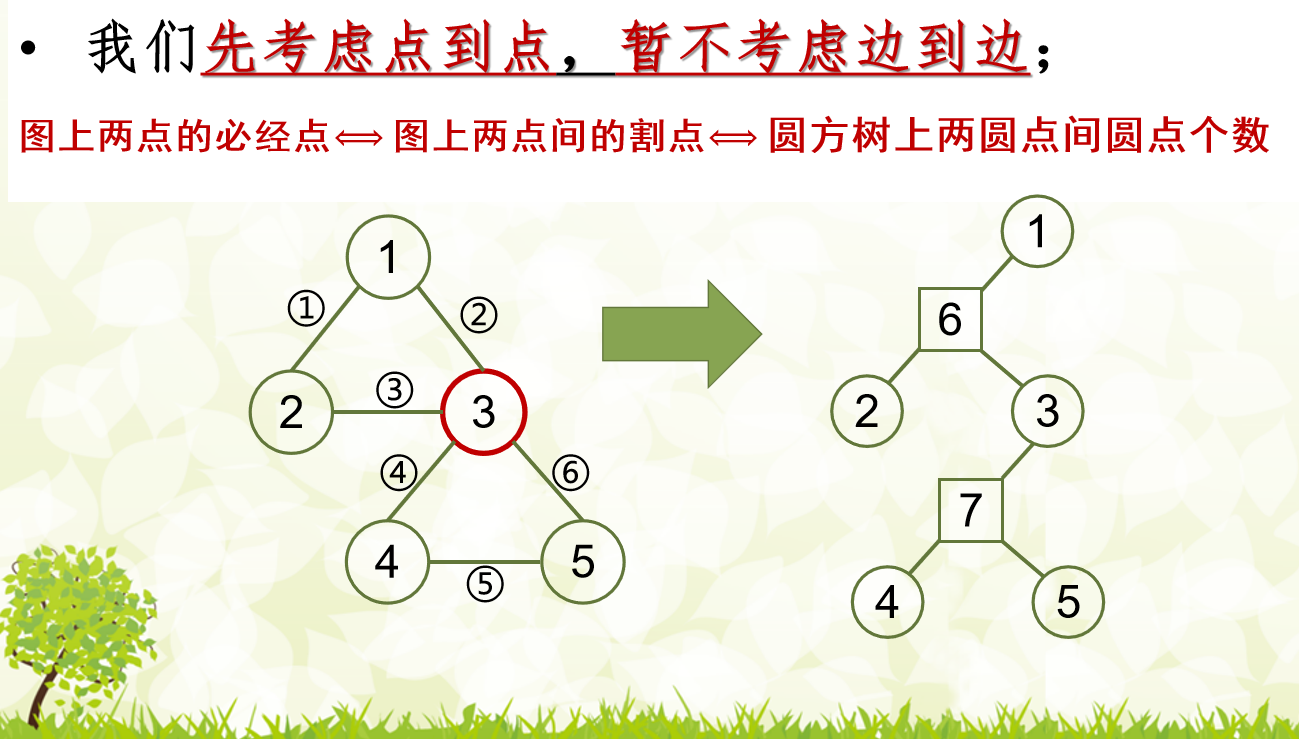
题目3642 [HDOJ 3686]交通实时查询系统
 6
评论 6
评论
2022-10-27 11:47:13
|
|
|
上述题目实际可以简化为:求一个节点 $1$ 到节点 $n$ 的路径,第 $k + 1$ 大的边权最小。是一个贪心的思想,很容易得出。 我们用 $f[u, k]$ 表示在节点 $1$ 到节点 $u$ 的路径中,用了 $k$ 次免费机会时,路径上最大的边权的最小值。 那么对于一个边 $u \to v$ 有以下状态转移:
这个状态转移显然有后效性,因为题目给出的并不一定是 DAG,确定不了遍历顺序。对于这种情况,我们使用 SPFA 来进行状态的转移。这样的最短路问题被称为 分层图最短路。用 SPFA 算法的时间复杂度是 $O(tNP)$,其中 $t$ 应该是一个比较小的常数,实际可以 AC 这一题。
题目147 [USACO Jan08] 架设电话线
AAAAAAAAAAAAA
 8
评论 8
评论
2022-10-27 11:21:43
|
|
|
算法一特殊样例: 1、长度小于 $5$ 的字符串不折叠, 因为压缩的话至少长度为 $4$; 例如:AAAA->4(A) 折叠前后相等 A->1(A) 不折叠更优 2、长度大于等于 $5$ 时,只包含一个字母; 例如:AAAAAAAAA->9(A)
算法二区间DP 设 $dp[i][j]$ 表示把区间 $[l, r]$ 内的字符压缩之后的最短长度,考虑两种操作: 1、合并两个小区间后变为一个大区间; 这显然就是区间 $dp$ 的套路方法,即: for (int k = l;k < r;++k) dp[l][r] = min (dp[l][r],dp[l][k] + dp[k + 1][r]); 2、将某个区间进行折叠; 对于 $[l,r]$ 字符串,若要被折叠成循环节长度为 $k$ 的字符串,需要满足 $1≤k≤r−l+1$ 且 $k ∣(r−l+1)$ 且 $∀i∈[l,r−k]$ $s[i]==s[i+k]$,若符合要求,则 $dp[l][r] = min (dp[l][r] , 2 + nums ((r - l + 1) / k) + dp[l][l + k - 1])$。其中的 $2$ 是两个括号的长度,$nums (x)$ 表示重复次数 $x$ 的位数,$dp[l][l + k - 1]$ 即循环节。
在得到最小长度后,由于需要输出合法的方案,所以我们在此基础上还要记录一些断点的信息,从而进行搜索。 用两个数组分别记录第一和第二种的操作的断点,第一种操作记录断点位置,第二种操作记录循环节的长度。 由于一个区间的处理只进行一种操作,所以在标记时要把另外一种操作的断点设为 0。
在递归时,对于一个区间若两种断点均不存在,则直接输出这段区间; 若是第一种操作的断点 k,则分别递归处理区间 [l,k] 和 [k+1,r]; 若是第二种,则先输出左括号和重复的次数,递归循环节的区间,再输出右括号即可。
//参考程序1:dp[][]记录最优长度,额外记录断点,递归输出方案
#include<bits/stdc++.h>
#define init(x,y) memset(x,y,sizeof(x))
#define INF 0x3f3f3f3f
using namespace std;
const int N = 105;
char str[N];
int n,dp[N][N],cut[N][N],fold[N][N];
int nums (int num)
{
int cnt = 0;
while (num) num /= 10,++cnt;
return cnt;
}
void check (int l,int r,int k)
{//[l,r]字符串是否可以折叠为长度为k的字符串
if ((r - l + 1) % k) return ;
for (int i = l;i <= r - k;++i)
if (str[i] != str[i + k]) return ;//不合法
int s = 2 + nums((r - l + 1) / k) + dp[l][l + k - 1];
if (s < dp[l][r])
{
dp[l][r] = s;
cut[l][r] = 0;
fold[l][r] = k;//区间可直接折叠
}
}
void dfs (int l,int r)
{//递归输出折叠方案
if (!cut[l][r] && !fold[l][r])//不能折叠,原样输出
for (int i = l;i <= r;++i) printf ("%c",str[i]);
else
if (cut[l][r])//有断点,分别递归两个区间
dfs (l,cut[l][r]),dfs (cut[l][r] + 1,r);
else//区间可直接折叠
{
printf ("%d(",(r - l + 1) / fold[l][r]);
dfs (l,l + fold[l][r] - 1);//继续递归循环节
printf (")");
}
}
int main ()
{
freopen ("folding.in","r",stdin);
freopen ("folding.out","w",stdout);
while (scanf ("%s",str + 1) != EOF)
{
n = strlen (str + 1);//从下标1开始存储
init (dp,INF);init (cut,0);init (fold,0);
for (int i = 1;i <= n;++i) dp[1][i] = i,dp[i][i] = 1;//初始化
for (int len = 1;len <= n;++len)
{//枚举区间长度
for (int l = 1;l <= n - len + 1;++l)
{//枚举区间左边界
int r = l + len-1;//右边界
//情况2:区间可直接折叠
for (int k = 1;k <= (r - l + 1) / 2;++k)
check(l,r,k);
//情况1:枚举断点,分别折叠左右区间后再合并
for (int k = l;k < r;++k)
{//枚举断点
if (dp[l][k] + dp[k + 1][r] < dp[l][r])//区间合并
{
dp[l][r] = dp[l][k] + dp[k + 1][r];
cut[l][r] = k;//记录断点
fold[l][r] = 0;
}
}
}
}
//printf ("%d\n",dp[1][n]);// 最小操作次数
dfs (1,n);//递归输出最优方案
puts ("\n");
}
return 0;
}
-----------------------------------------------------------------------------------------------------------------------------
//参考程序2:dp[l][r]直接存最优方案;
#include <bits/stdc++.h>
using namespace std;
string dp[110][110], s;
string _to_string(int num) {
string ans;
while(num) {
ans += num % 10 + '0';
num /= 10;
}
reverse(ans.begin(), ans.end());
return ans;
}
int main() {
freopen("folding.in","r",stdin);
freopen("folding.out","w",stdout);
int n;
while(cin >> s) {
n = s.length();
for (int i = 0; i < n; i++) {
dp[i][i] = s[i];//初始化
}
for (int len = 2; len <= n; len++)
{//枚举区间长度
for (int lt = 0; lt < n - len + 1; lt++)
{//枚举区间左边界
int rt = lt + len - 1;//枚举区间右边界
dp[lt][rt] = s.substr(lt, rt - lt + 1);//初始化
for (int loop = 1; loop <= len / 2; loop++)
{//枚举循环节长度,检测区间是否可以直接折叠
if(len % loop) continue;
int l = lt, r = lt + loop;
while(s[l] == s[r] && r <= rt) l++, r++;
if(r > rt)
{
int num = len / loop;//循环次数
dp[lt][rt] = _to_string(num);
dp[lt][rt] += "(";
dp[lt][rt] += dp[lt][lt + loop - 1];
dp[lt][rt] += ")";
//cout<< dp[lt][rt] <<endl;
break;
}
}
for (int k = lt; k < rt; k++)//区间DP
{//枚举断点,分别折叠左右子区间后再合并
if(dp[lt][rt].length() > dp[lt][k].length() + dp[k + 1][rt].length() || dp[lt][rt].length() == 0)
{
dp[lt][rt] = dp[lt][k] + dp[k + 1][rt];
}
}
}
}
cout << dp[0][n - 1] <<endl;
}
return 0;
}
题目2996 [POJ 2176]折叠字符串(Folding)
 8
评论 8
评论
2022-10-27 10:58:33
|
|
|
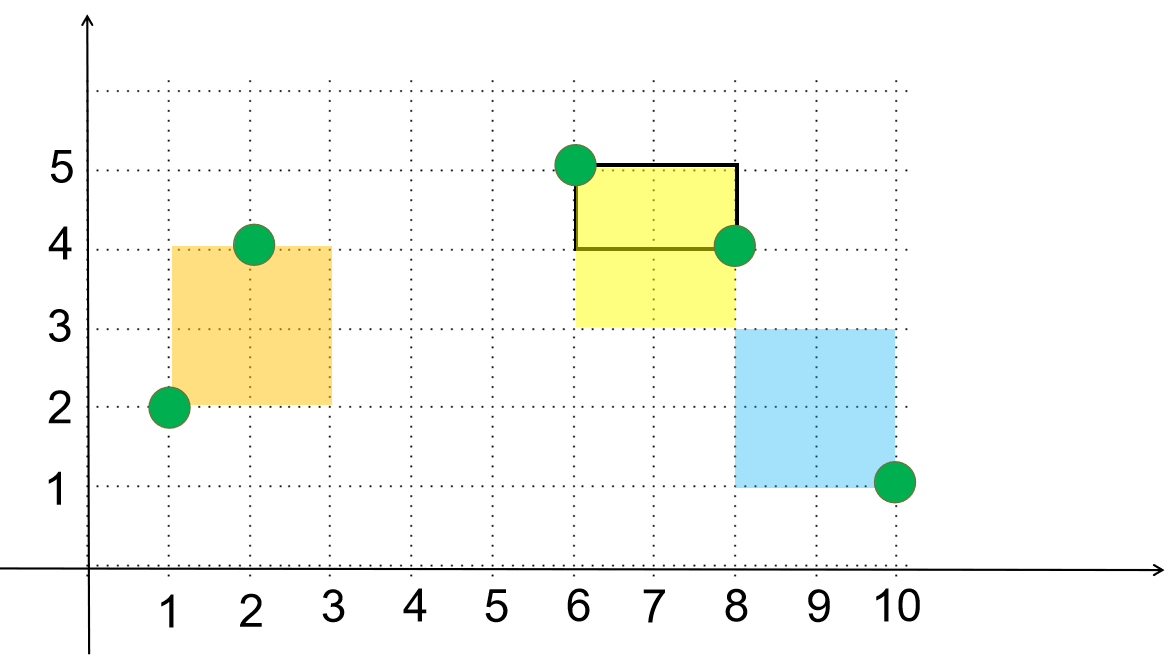
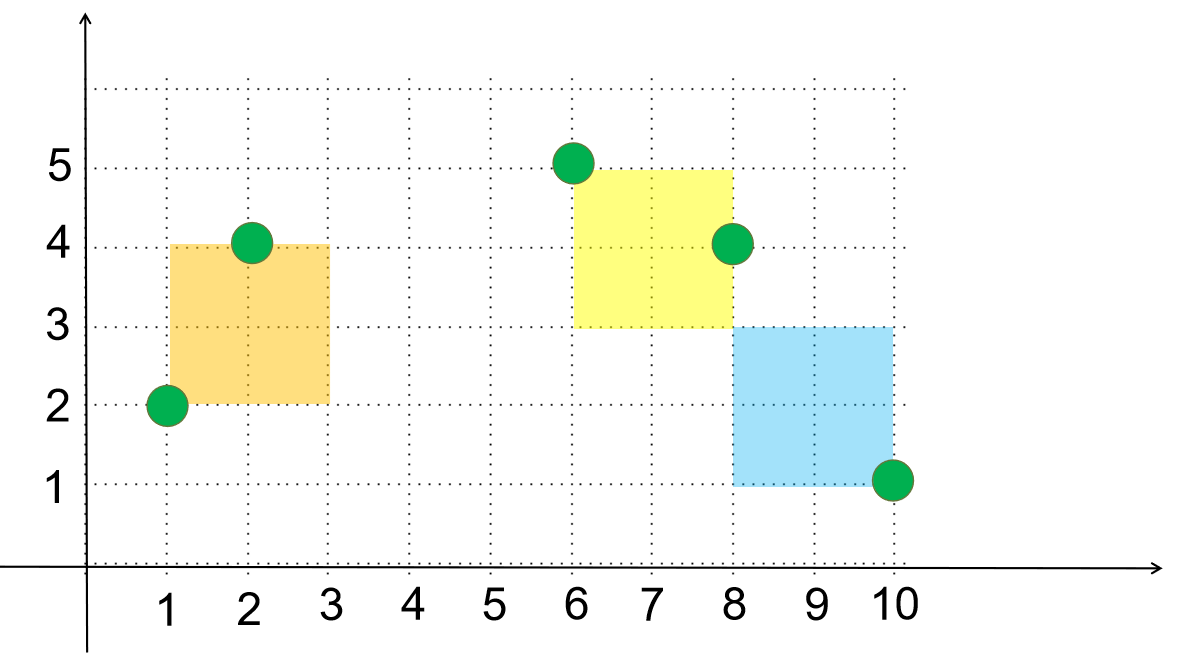
(实际上是我比赛时的草稿,可能会有些跳跃,不过总体应该还算清晰) $y$ 表示扩大后的长减去 $\Delta y$,$x$ 同理 下面是思路:
最小情况: 所有三角形的斜边作为向量相加为对角线(斜边为路线),则三角形最小时直角顶点为 $ (x_i, y_i) $ 相似 => $\displaystyle\frac{y}{\Delta x} = \frac{a_i}{b_i}, \frac{x}{\Delta y} = \frac{b_i}{a_i} $ => $ \displaystyle{ a_i \Delta x + b_i \Delta y = k }$ 故 k 的最小值大于等于左式 $ \displaystyle{ a_i \times (x_i - x_{i - 1}) + b_i \times (y_i - y_{i - 1}) \leq k }$ 移项,得 $ \displaystyle{ y_i \le \frac{k - a_i \times (x_i - x_{i - 1})}{b_i} + y_{i - 1} }$ 观察三角形,易得(画出来的话可能会直观一点) $ \displaystyle{ \frac{k}{a_i} \ge \Delta x = x_i - x_{i - 1} \\ \text{于是有} \\ x_{i - 1} \ge x_i - \frac{k}{a_i} }$ 又 $ \displaystyle{ x_i - x_{i - 1} \ge 0 } $ 所以 $ \displaystyle{ x_i \ge x_{i - 1} \ge x_i - \frac{k}{a_i} } $ 接下来,由得到的这两组不等式就可以求得答案了,即枚举除定值外的 $i, x_i, x_{i - 1}, k$ 如果因变量 $y_i$ 大于等于 $m$,就满足题目要求。 具体来说,最外面枚举 $k$,然后枚举积木,横坐标,得到 $y_n$ 的最大值,然后和 $m$ 比较,找到最小的 $k$。 根据上面的描述,不难想到状态表示:$f[i, j]$ 表示枚举到第 $i$ 个积木,横坐标枚举到 $j$ 时纵坐标的最大值,最后和 $m$ 比较的是 $f[n, m]$。 最后,只是简单的枚举其实还不能通过这一题,因为我们并不知道答案的具体取值范围,如果是 $1 \times 10^9$ 的级别,枚举一万年也算不出来,因为我们是要找最小的满足条件的 $k$(大于这个值的都满足条件),所以对于 $k$,我们用二分来找到答案。 最后的时间复杂度应该是 $O(nm^2 \log r) \ (r \text{ 取你取的二分边界})$
题目3629 [LOJ β Round]ZQC 的拼图
AAAAAAAAAA
 8
评论 8
评论
2022-10-24 23:49:43
|