|
|
2156. [BZOJ 4407] 于神之怒加强版 - 题解题意给定 $n, m, k$,求 $\sum_{i=1}^n\sum_{j=1}^m\gcd(i,j)^k$ 模 $10^9+7$ 的结果。$T$ 组数据。($n,m,k\sim5\times10^6$,$T\sim2\times10^3$) 推导过程令 $n\le m$ $$\begin{aligned}&\quad\sum_{i=1}^n\sum_{j=1}^m\gcd(i,j)^k\\&=\sum_{d=1}^n\sum_{i=1}^{\lfloor\frac n d\rfloor}\sum_{j=1}^{\lfloor\frac m d\rfloor}d^k\cdot[\gcd(i,j)=1]\\&=\sum_{d=1}^n\sum_{i=1}^{\lfloor\frac n d\rfloor}\sum_{j=1}^{\lfloor\frac m d\rfloor}d^k\sum_{p\mid i,j}\mu(p)\\&=\sum_{d=1}^nd^k\sum_{i=1}^{\lfloor\frac n d\rfloor}\sum_{j=1}^{\lfloor\frac m d\rfloor}\sum_{p\mid i,j}\mu(p)\\&=\sum_{d=1}^nd^k\sum_{p=1}^{\lfloor\frac n d\rfloor}\mu(p)\left\lfloor\frac n{dp}\right\rfloor\left\lfloor\frac m{dp}\right\rfloor\\&\text{令}D=dp\\&=\sum_{D=1}^n\left\lfloor\frac n D\right\rfloor\left\lfloor\frac m D\right\rfloor\sum_{d\mid D}d^k\mu\left(\frac D d\right)\end{aligned}$$ 前面的 $\displaystyle\sum_{D=1}^n\left\lfloor\frac n D\right\rfloor\left\lfloor\frac m D\right\rfloor$ 使用整除分块,仅需求后面 $\displaystyle\sum_{d\mid D}d^k\mu\left(\frac D d\right)$;设 $f(D)=\displaystyle\sum_{d\mid D}d^k\mu\left(\frac D d\right)$,显然 $f(D)$ 是积性函数,设 $D=\prod p_i^{c_i}$,则有: $$\begin{aligned}f(D)&=f\left(\prod p_i^{c_i}\right)\\&=\prod f\left(p_i^{c_i}\right)\\&=\prod\left[1^k\mu(p_i^{c_i})+p_i^k\mu(p_i^{c_i-1})+p_i^{2k}\mu(p_i^{c_i-2})+\cdots+p_i^{(c_i-1)k}\mu(p_i)+p_i^{c_ik}\mu(1)\right]\\&=\prod\left[p_i^{c_ik}-p_i^{(c_i-1)k}\right]\\&=\prod\left[p_i^{(c_i-1)k}(p_i^k-1)\right]\end{aligned}$$ 线性筛即可。 详细解释原式如下: $$\sum_{i=1}^n\sum_{j=1}^m\gcd(i,j)^k$$ 可令 $n\le m$,若 $n>m$ 直接交换即可。 首先枚举 $\gcd(i,j)$ 可能等于的数,即 $1$ 到 $n$(因为 $n\le m$)。也就是枚举 $d$,当 $\gcd(i,j)=d$ 时才会产生贡献,即: $$\sum_{d=1}^n\sum_{i=1}^n\sum_{j=1}^md^k[\gcd(i,j)=d]$$ 因为 $i$ 是从 $1$ 到 $n$ 的数字,$d$ 也是从 $1$ 到 $n$ 的数字,所以可以用 $d$ 乘上一个 $1$ 到 $n/d$ 的数来表示 $1$ 到 $n$ 的数,$m$ 同理: $$\sum_{d=1}^n\sum_{i=1}^{\lfloor\frac n d\rfloor}\sum_{j=1}^{\lfloor\frac m d\rfloor}d^k[\gcd(i\times d,j\times d)=d]$$ 既然 $i\times d$ 与 $j\times d$ 已经有了公共的因数 $d$,那么要使这俩最大公约数为 $d$ 的话,一定有 $\gcd(i,j)=1$: $$\sum_{d=1}^n\sum_{i=1}^{\lfloor\frac n d\rfloor}\sum_{j=1}^{\lfloor\frac m d\rfloor}d^k[\gcd(i,j)=1]$$ 因为 $\mu*1=\varepsilon$,即 $\sum_{d\mid n}\mu(d)=[n=1]$,替换掉上式的艾弗森括号: $$\sum_{d=1}^n\sum_{i=1}^{\lfloor\frac n d\rfloor}\sum_{j=1}^{\lfloor\frac m d\rfloor}d^k\sum_{p\mid i,j}\mu(d)$$ $d$ 的取值至于第一层求和有关,与第二、三层求和无关,故可以把 $d^k$ 提到前面: $$\sum_{d=1}^nd^k\sum_{i=1}^{\lfloor\frac n d\rfloor}\sum_{j=1}^{\lfloor\frac m d\rfloor}\sum_{p\mid i,j}\mu(p)$$ 与其枚举 $i,j$,不如只枚举 $\mu(p)$ 会出现多少次,如果固定了 $p$,那么在 $i$ 在遍历 $1$ 到 $\lfloor\frac n d\rfloor$ 时,会出现 $\lfloor\frac n{dp}\rfloor$ 次 $p$,或者说 $1$ 到 $\lfloor\frac n d\rfloor$ 中有 $\lfloor\frac n{dp}\rfloor$ 个数是 $p$ 的倍数($j$ 同理)。因为 $p$ 是 $i,j$ 的因数且 $i$ 的枚举范围小于 $j$ 的枚举范围(因为 $n\le m$),所以 $p$ 的枚举范围和 $i$ 相同: $$\sum_{d=1}^nd^k\sum_{p=1}^{\lfloor\frac n d\rfloor}\mu(p)\sum_{i=1}^{\lfloor\frac n{dp}\rfloor}\sum_{j=1}^{\lfloor\frac m{dp}\rfloor}1$$ 后面两个求和已经能直接算出来了: $$\sum_{d=1}^nd^k\sum_{p=1}^{\lfloor\frac n d\rfloor}\mu(p)\left\lfloor\frac n{dp}\right\rfloor\left\lfloor\frac m{dp}\right\rfloor$$ 令 $D=dp$,转为枚举 $D$ 之后 $\lfloor\frac n{dp}\rfloor\lfloor\frac m{dp}\rfloor$ 就可以直接提出来;$p=D/d$,所以 $\mu(p)$ 被替换成 $\mu(D/d)$;第二层循环与 $d$ 无关,所以 $d^k$ 可以提到第二层循环;此时第二层循环里面就变成了 $d^k\mu(D/d)$,因为 $d=D/p$,所以 $d$ 的枚举范围就是 $d\mid D$: $$\sum_{D=1}^n\left\lfloor\frac n D\right\rfloor\left\lfloor\frac m D\right\rfloor\sum_{d\mid D}d^k\mu\left(\frac D d\right)$$ 观察前面的 $\sum_{D=1}^n\lfloor\frac n D\rfloor\lfloor\frac m D\rfloor$ 可以想到用整除分块做,但是想要用整除分块,需要知道后面 $\sum_{d\mid D}d^k\mu(\frac D d)$ 的前缀和(整体的,指在 $D$ 取 $1,2,3\cdots$ 时整个求和结果的前缀和),那就单独来研究它。 令 $$f(D)=\sum_{d\mid D}d^k\mu\left(\frac D d\right)$$ $d^k$ 其实就是恒等函数 $\text{id}_k(d)$,$\mu(\frac D d)$ 就是欧拉函数 $\mu(\frac D d)$,那 $f(D)$ 不就是 $\text{id}_k$ 和 $\mu$ 的狄利克雷卷积嘛! $$f(D)=\sum_{d\mid D}d^k\mu\left(\frac D d\right)=(\text{id}_k*\mu)(D)$$ 狄利克雷卷积具有积性保持性(狄利克雷生成函数 - OI Wiki),所以 $f(D)$ 也是积性函数!那就好办了!如果想求 $F(D)$ 的话(注意!上面那个式子 $f(D)$ 表示一个关于 $D$ 的函数,$D$ 是变量,而现在说的 $D$ 是一个给定的常数!),不妨设 $D=\prod p_i^{c_i}$,则根据积性函数的定义: $$f(D)=f\left(\prod p_i^{c_i}\right)=\prod f(p_i^{c_i})$$ 把 $f(p_i^{c_i})$ 都带入 $f(D)=\sum_{d\mid D}d^k\mu(\frac D d)$(同样,这里的 $D$ 只是一个函数中的自变量,与上面那个式子中的 $D$ 含义不同!): $$\prod\left[1^k\mu(p_i^{c_i})+p_i^k\mu(p_i^{c_i-1})+p_i^{2k}\mu(p_i^{c_i-2})+\cdots+p_i^{(c_i-1)k}\mu(p_i)+p_i^{c_ik}\mu(1)\right]$$ 因为 $p_i$ 是质数,根据莫比乌斯函数的定义([莫比乌斯反演 - OI Wiki](https://oiwiki.com/math/number-theory/mobius/#定义)),当 $x$ 含有平方因子时 $\mu(x)=0$,那么 $\mu(p_i^{c_i}),\mu(p_i^{c_i-1}),\mu(p_i^{c_i-2})\cdots\mu(p_i^2)$ 都等于 $0$!带入到上式: $$\prod\left[p_i^{c_ik}-p_i^{(c_i-1)k}\right]$$ 居然只剩这么两项了!镇棒!把 $p_i^{(c_i-1)k}$ 给提出来: $$\prod\left[p_i^{(c_i-1)k}(p_i^k-1)\right]$$ 所以,我们得到了函数 $f(D)$ 的表达式: $$f(D)=\prod\left[p_i^{(c_i-1)k}(p_i^k-1)\right]$$ 哇哇!这样不就可以线性筛了嘛!为什么呢?看看线性筛的代码: void solve(int n) {
for (int i = 2; i <= n; ++i) {
if (!vis[i]) {
primes.push_back(i);
// 更新 f[i] 值
}
for (int p : primes) {
if (i * p > n) break;
vis[i * p] = 1;
if (i % p == 0) {
// 更新 f[i] 值
break;
} else {
// 更新 f[i] 值
}
}
}
}
假如说现在 $i$ 是质数,程序运行到第 5 行,根据上面得到的式子:$f(D)=\prod[p_i^{(c_i-1)k}(p_i^k-1)]$,这个时候 $p_i=i$ 且 $c_i=1$,那 $f(i)$ 就等于 $p_i^k-1$ 也就是 $i^k-1$。
if (!vis[i]) {
primes.push_back(i);
f[i] = (kasumi(i, k) - 1 + MOD) % MOD;
}
到了下面筛 $i\times p$ 时,假如 $i\bmod p\neq0$,也就是 $p$ 不是 $i$ 的因数,$i$ 乘上 $p$ 之后为 $i$ 多添加了一个全新的因数,而且这个因数还是个质数(根据线性筛的定义,每个数只被它最小的质因数筛去(筛法 - OI Wiki)),那么根据刚才的式子:$f(D)=\prod[p_i^{(c_i-1)k}(p_i^k-1)]$,乘积中多添加了 $p^{(c-1)k}(p^k-1)$ 这一项。因为 $p$ 是新添加的因数,所以 $c=1$,那 $p^{(c-1)k}=1$,相当于在乘积中只多添加了 $p^k-1$ 这一项(又或者说是添加了 $f(p)$ 这一项,因为 $p$ 是质数,则 $f(p)=p^k-1$;另一种解释是 $\gcd(i,p)=1$,所以根据积性函数的定义也能得证。),则 $f(i\times p)=f(i)(p^k-1)$(或 $f(i\times p)=f(i)f(p)$)。
if (i % p == 0) {
// ...
break;
} else {
f[i * p] = f[i] * (kasumi(p, k) - 1 + MOD) % MOD; // 或 f[i * p] = f[i] * f[p] % MOD;
}
那如果 $i\bmod p=0$ 呢?也就是 $p\mid i$,$p$ 在 $i$ 的质因数中已经出现过了,$i$ 乘上 $p$ 之后相当于把 $p$ 这个质因数的指数加了 $1$,那么根据上式 $f(D)=\prod[p_i^{(c_i-1)k}(p_i^k-1)]$,$i$ 乘 $p$ 相当于把 $c_i$ 加 $1$,相当于在乘积中添加了 $p_i^k$ 这一项($\displaystyle\frac{p_i^{(c_i+1-1)k}(p_i^k-1)}{p_i^{(c_i-1)k}(p_i^k-1)}=p_i^k$),则 $f(i\times p)=f(i)p_i^k$。 if (i % p == 0) {
f[i * p] = f[i] * kasumi(p, k) % MOD;
break;
} else {
// ...
}
终于解决完 $f(D)$ 的问题啦,回到原来的答案式: $$\sum_{D=1}^n\left\lfloor\frac n D\right\rfloor\left\lfloor\frac m D\right\rfloor f(D)$$ 因为线性筛时涉及到快速幂,那么只能用 $O(n\log_2k)$ 的时间复杂度求出 $f(D)$ 即其前缀和,加上整除分块,可以用 $O(\sqrt n)$ 的时间复杂度求出答案式。那么整体的时间复杂度就是 $\Theta(n\log_2k+T\sqrt n)$,$\Omega(n\log_2k)$。 代码#include <cstdio>
#include <vector>
#include <algorithm>
typedef long long ll;
const int MAXN = 5e6 + 10;
const int MOD = 1e9 + 7;
ll kasumi(ll x, ll y) {
ll res = 1;
while (y) {
if (y & 1) res = res * x % MOD;
y >>= 1;
x = x * x % MOD;
}
return res;
}
ll k;
bool vis[MAXN];
ll f[MAXN];
::std::vector <ll> primes, mi;
void solve(ll n) {
f[1] = 1;
for (ll i = 2; i <= n; ++i) {
if (!vis[i]) {
primes.push_back(i);
f[i] = (kasumi(i, k) - 1 + MOD) % MOD;
}
for (ll p : primes) {
if (i * p > n) break;
vis[i * p] = 1;
if (i % p == 0) {
f[i * p] = f[i] * kasumi(p, k) % MOD;
break;
} else {
f[i * p] = f[i] * f[p] % MOD; /* kasumi(p, k) - 1*/
}
}
}
for (ll i = 1; i <= n; ++i) {
f[i] = (f[i] + f[i - 1]) % MOD;
}
}
int T;
ll n, m;
ll ans;
int main() {
freopen("bzoj_4407.in", "r", stdin);
freopen("bzoj_4407.out", "w", stdout);
scanf("%d %lld", &T, &k);
solve(MAXN - 10);
while (T--) {
scanf("%lld %lld", &n, &m);
if (n > m) n ^= m ^= n ^= m;
ans = 0;
for (ll i = 1, ed; i <= n; i = ed + 1) {
ed = ::std::min(n / (n / i), m / (m / i));
ans = (ans + (n / i) * (m / i) % MOD * (f[ed] - f[i - 1] + MOD) % MOD) % MOD;
}
printf("%lld\n", ans);
}
return 0;
}
Update
题目2156 [BZOJ 4407] 于神之怒加强版
AAAAAAAAAA
 5
1 条 评论 5
1 条 评论
2025-06-20 20:19:20
|
|
|
Pro4034 罚站 题解
×
…提示!该题解未通过审核,建议分享者本着启发他人,照亮自己的初衷以图文并茂形式完善之,请勿粘贴代码。........................................................................ 该题解等待再次审核........................................................................(剩余 0 个中英字符)
题目4034 罚站
AAAAAAAAAA
2025-06-02 18:24:29
|
|
|
$题目大意$ ${求}\sum_{i=1}^{n}\sum _{j=1}^{m}{lcm(i,j)} {且} 1\le n,m\le 1e7$ ${正解:}$ ${有}{lcm(i,j)=\frac{i\cdot j}{\gcd(i,j)}}$ ${所以原式为:}$ $ans(n,m)=\sum_{i=1}^{n}\sum _{j=1}^{m}{\frac{i\cdot j}{\gcd(i,j)}}$ $~\qquad\qquad =\sum_{i=1}^{n}\sum _{j=1}^{m}{ \sum_{d\mid i,d\mid j,\gcd(\frac{i}{d},\frac{j}{d})}{}{\frac{i\cdot j}{d}}}$ ${现在需要将d给提出来,默认}{n\le m,}{我们设}i=i'\cdot d,j=j'\cdot d,{则}i'=\frac{i}{d},j'=\frac{j}{d},将i,j替换进上式得:$ $ans(n,m)=\sum_{d=1}^{\min(n,m)}{\sum_{i'=1}^{\left \lfloor \frac{n}{d} \right \rfloor}{\sum_{j'=1}^{\left \lfloor \frac{m}{d} \right \rfloor}{[\gcd(i',j')=1]\cdot d\cdot i'\cdot j'}}}$ $~\qquad\qquad=\sum_{d=1}^{n}{d\cdot\sum_{i=1}^{\left \lfloor \frac{n}{d} \right \rfloor}{\sum_{j=1}^{\left \lfloor \frac{m}{d} \right \rfloor}{[\gcd(i,j)=1]\cdot i\cdot j}}}$ ${接着将d后面的部分再提出来考虑,化简枚举约数,运用莫比乌斯反演:} [\gcd(i,j)=1]=\sum_{d\mid gcd}{\mu{(d)}}:$ ${设} \ {g(n,m)}=\sum_{i=1}^{n}{\sum_{j=1}^{m}{[\gcd(i,j)=1]\cdot i\cdot j}}$ $~\qquad\qquad=\sum_{d=1}^{n}{\sum_{d\mid i}^{n}{\sum_{d\mid j}^{m}{\mu(d)\cdot i\cdot j}}}$ ${再设}\ i=i' \cdot d,j=j' \cdot d \ {带入,将}\mu{提出来}$ ${即}\ g(n,m)=\sum_{d=1}^{n}{\mu(d)}\cdot{d^{2}\cdot{\sum_{i=1}^{\left\lfloor \frac{n}{d} \right \rfloor}{\sum_{j=1}^{\left \lfloor \frac{m}{d} \right \rfloor}{i\cdot j}}}}$ $~\qquad\qquad = \sum_{d=1}^{n}{\mu(d)}\cdot{d^{2}}\cdot\frac{{\left \lfloor \frac{n}{d} \right \rfloor}\cdot ({\left \lfloor \frac{n}{d} \right \rfloor}+1)\cdot {\left \lfloor \frac{m}{d} \right \rfloor}\cdot({\left \lfloor \frac{m}{d} \right \rfloor}+1)}{4}$ ${最后将g(n,m)带入ans(n,m)中得:}$ $ans(n,m)=\sum_{d=1}^{n}{d}\cdot{g(\left\lfloor \frac{n}{d}\right\rfloor,\left\lfloor \frac{m}{d}\right\rfloor)}$ ${用数论分块求出来}~{g(n,m)}~{再用数论分块求出来}~{ans(n,m),}~{就在{\Theta(n+m)内}}{得到答案了}~{(∠・ω< )⌒★}$
题目1886 [国家集训队 2011] Crash的数字表格
AAAAAAAAAAAAAAAAAAAA
 3
1 条 评论 3
1 条 评论
2025-05-24 21:56:25
|
|
|
Pro896 圈奶牛 题解896. 圈奶牛 题解题意描述给定有 n 头奶牛,要把这些奶牛用栅栏围起来,栅栏的总长度即为花费,求花费的最小值。 题解例如有这么几头牛:
显然,一个想法是用一个圈把这些牛全部围起来:
但是这样显然不是花费最小的,那我们就让这个椭圆一直缩小,直到和边缘上的点碰触就停止缩小:
这样就是花费最小的啦! 如果再往里缩小的话,花费就会反而变长!
如图,在 $\triangle GHI$ 中,根据三边关系显然有 $GI + IH \gt GH$,所以 $GH$ 就是 $G$ 到 $H$ 花费最小的连接方式。
注意到这个连接方式的顶点连线的斜率是递减的 即: $$k_{HG} > k_{GE} > k_{ED} > k_{HD}$$ 那么,我们如何找到这个连接方式呢? 首先找到一个 $x$ 坐标或 $y$ 坐标最大/最小的点,例如图中的点 $H$、点 $G$、点 $E$、点 $D$。 我们以点 $H$ 为例,将这些点排序,按照其他点与点 $H$ 的连线的斜率降序排序(从小到大也可以,只不过实现略有不同):
struct NODE {
double x, y;
} node[MAXN];
double getk(NODE x, NODE y) {
return (x.y - y.y) / (x.x - y.x);
}
int main() {
... // 读入
sort(node + 1, node + n + 1, [](NODE x, NODE y) {
if (x.x != y.x) return x.x < y.x;
return x.y > y.y;
}); // 先进行一个排序,按照 x 坐标为第一关键字升序
// y 坐标为第二关键字降序,也就是要把最左上角的点放到第一个
sort(node + 2, node + n + 1, [](NODE x, NODE y) {
return getk(x, node[1]) > getk(y, node[1]);
});
}
但是 [code](x.x - y.x)[\code] 容易等于零,除数等于零就错误了!那我们就将除法比较改成乘法叭 也就是: $$\frac{a_{1,y} - a_{2,y}}{a_{1,x} - a_{2.x}} \le \frac{b_{1,y} - b_{2,y}}{b_{1,x} - b_{2,x}} \\ \Downarrow \\ (a_{1,y} - a_{2,y})(b_{1,x} - b_{2,x}) \le (b_{1,y} - b_{2,y})(a_{1,x} - a_{2.x})$$
struct NODE {
double x, y;
} node[MAXN];
bool check(NODE a1, NODE a2, NODE b1, NODE b2) {
return (a1.y - a2.y) * (b1.x - b2.x) <= (b1.y - b2.y) * (a1.x - a2.x);
}
double dis(NODE x, NODE y) {
return sqrt(pow(x.x - y.x, 2) + pow(x.y - y.y, 2));
}
int main() {
...
// 找到左上角的点
sort(node + 1, node + n + 1, [](NODE x, NODE y) {
if (x.x != y.x) return x.x < y.x;
return x.y > y.y;
});
// 其余点按照与左上角的点连线的斜率降序排列
sort(node + 2, node + n + 1, [](NODE x, NODE y) {
return !check(x, node[1], y, node[1]);
});
...
}
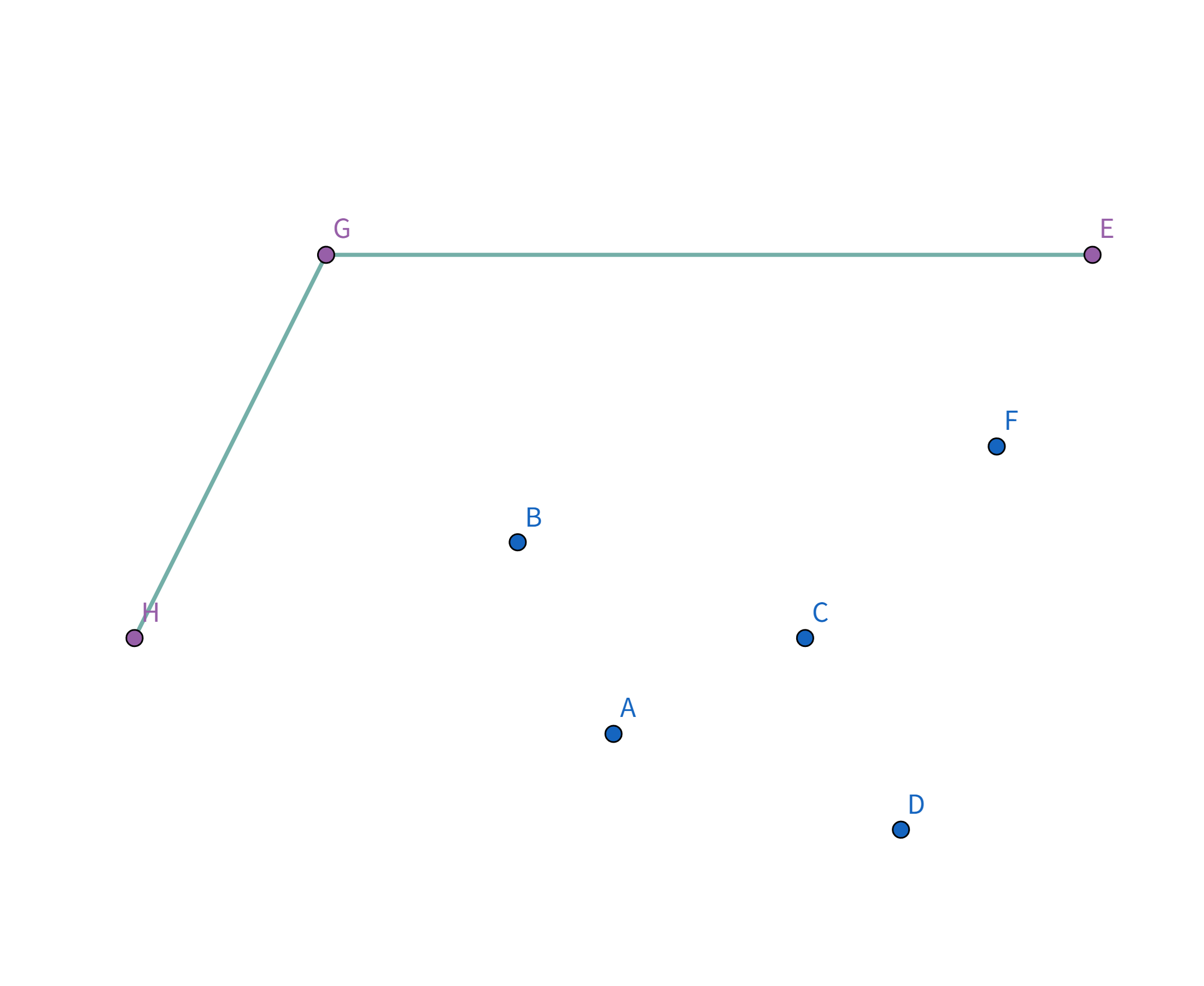
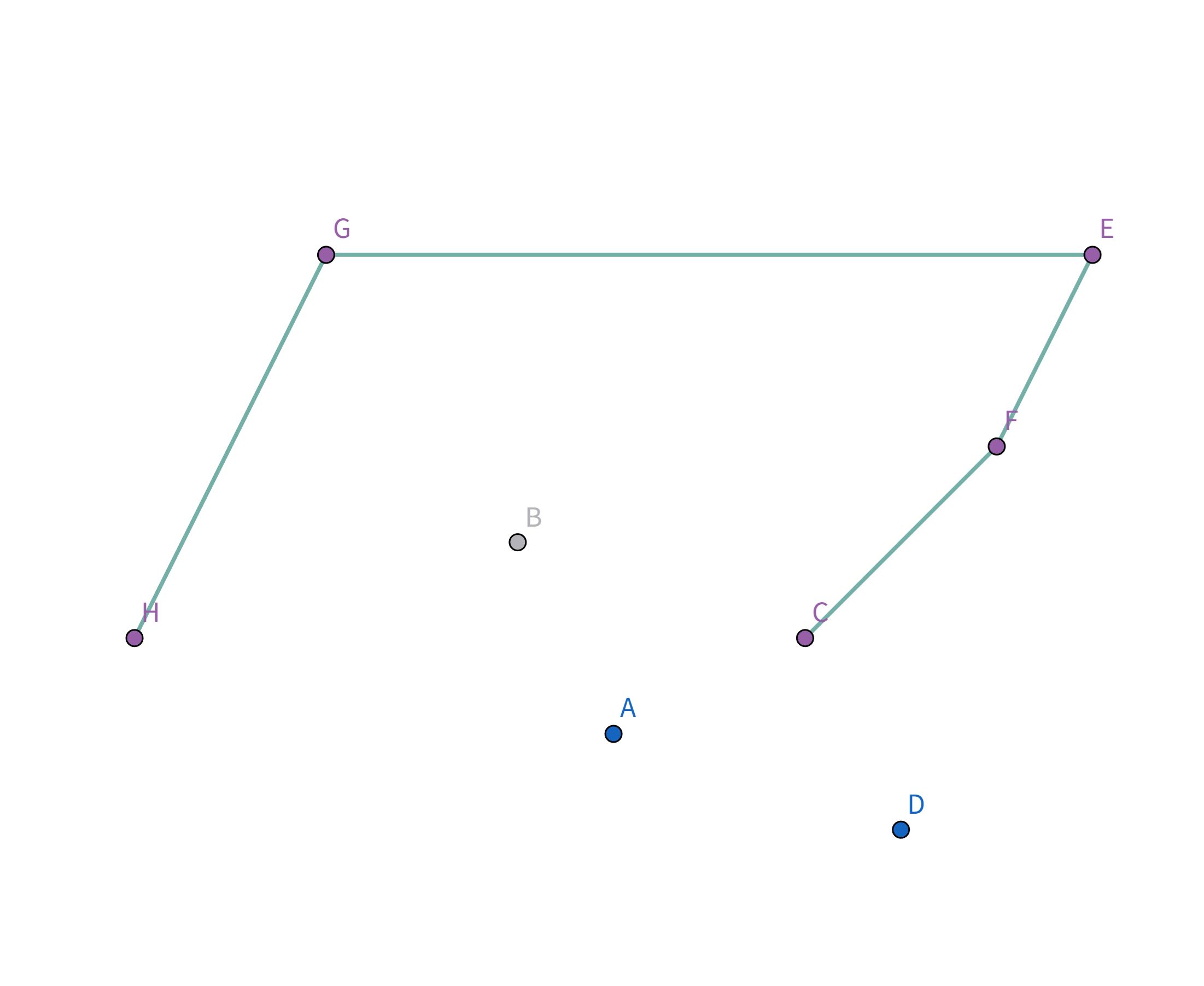
接下来就是考虑怎么样把 $G,H,D,E$ 四个点选中啦! 我们用一个栈来维护选中的点。 首先点集是这样的:
按照排序后的顺序取扫描,首先扫描到点 $H$,此时栈为空,直接把点 $H$ 加入栈:
接着扫描到点 $G$,站内只有一个元素,直接把点 $G$ 加入栈:
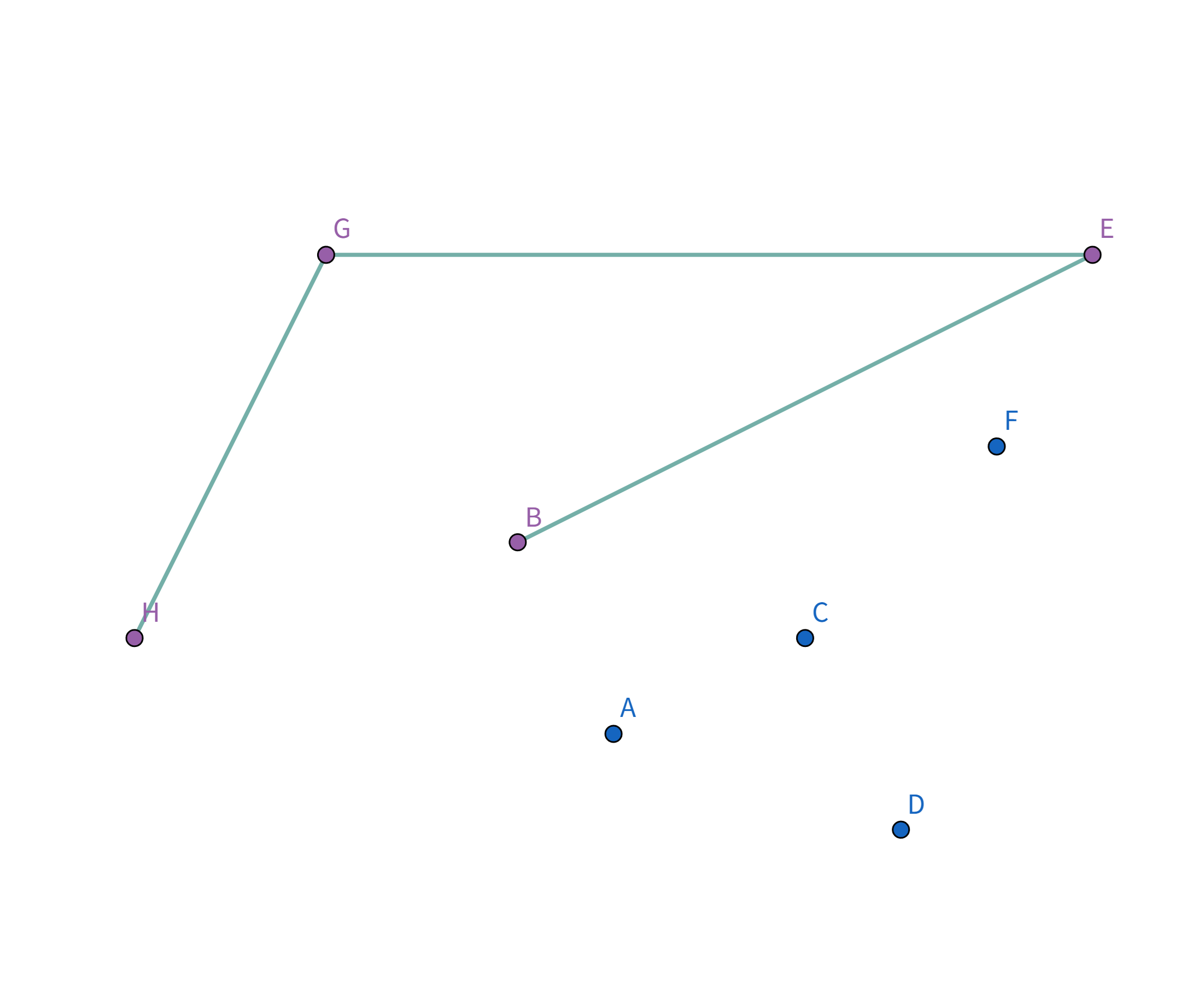
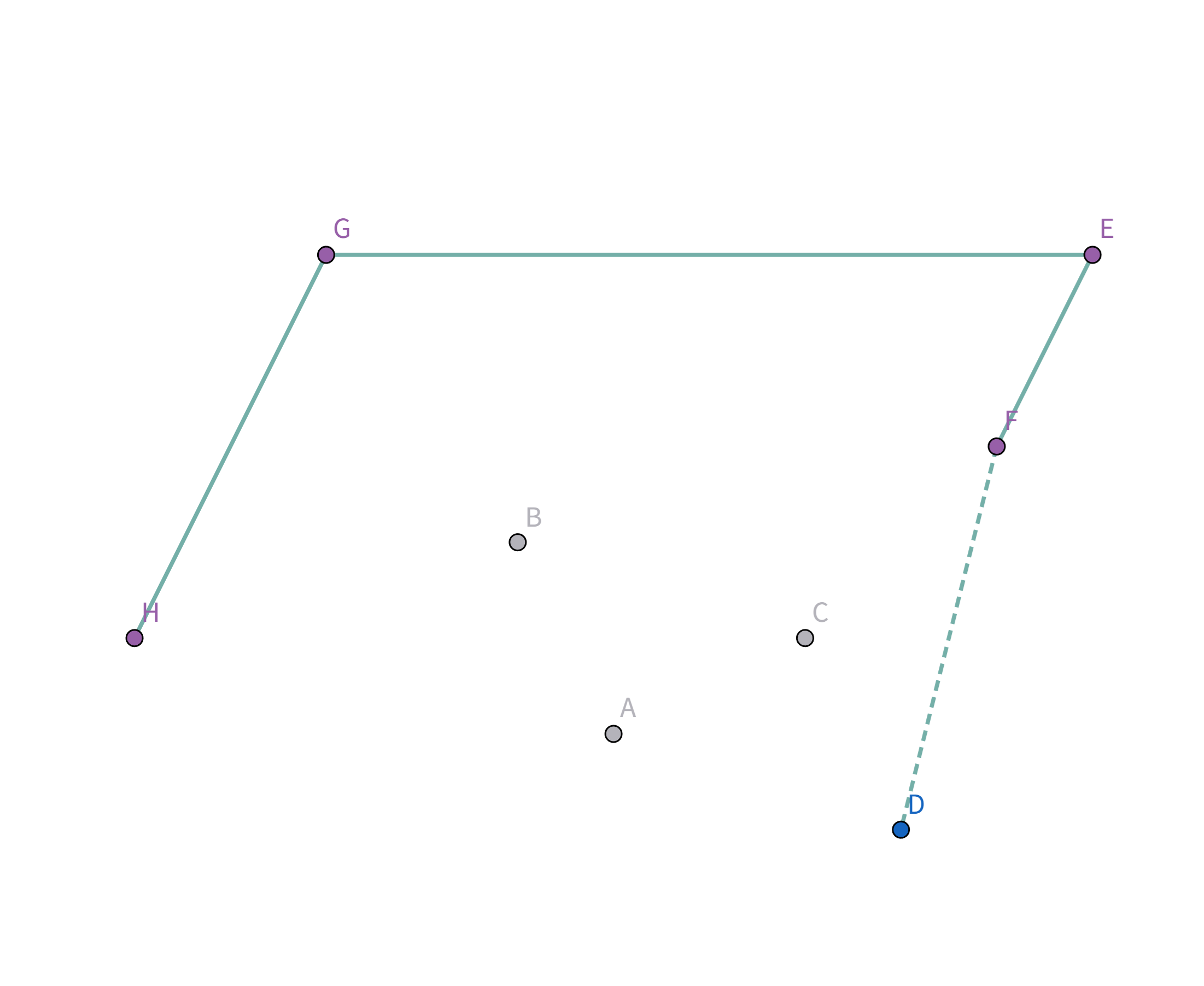
接着扫描到点 $E$,发现其与栈顶的点 $G$ 连线的斜率 与之前的所有连线的斜率 满足递减关系,直接入栈:
接着扫描到点 $B$,发现其与栈顶的点 $E$ 连线的斜率 与之前的所有连线的斜率 满足递减关系,直接入栈:
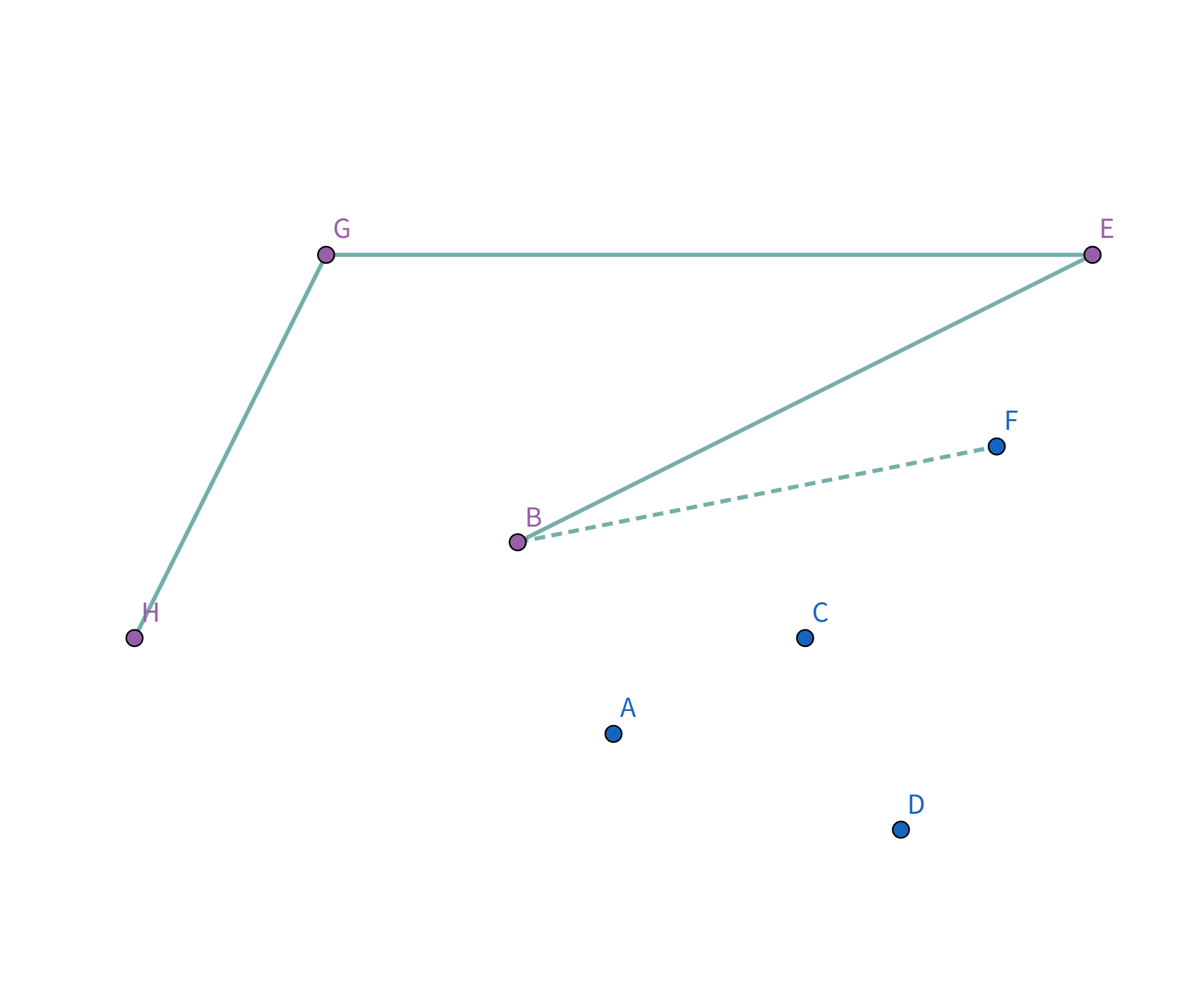
接着扫描到点 $F$!它与栈顶的点 $B$ 的连线斜率比之前大了!
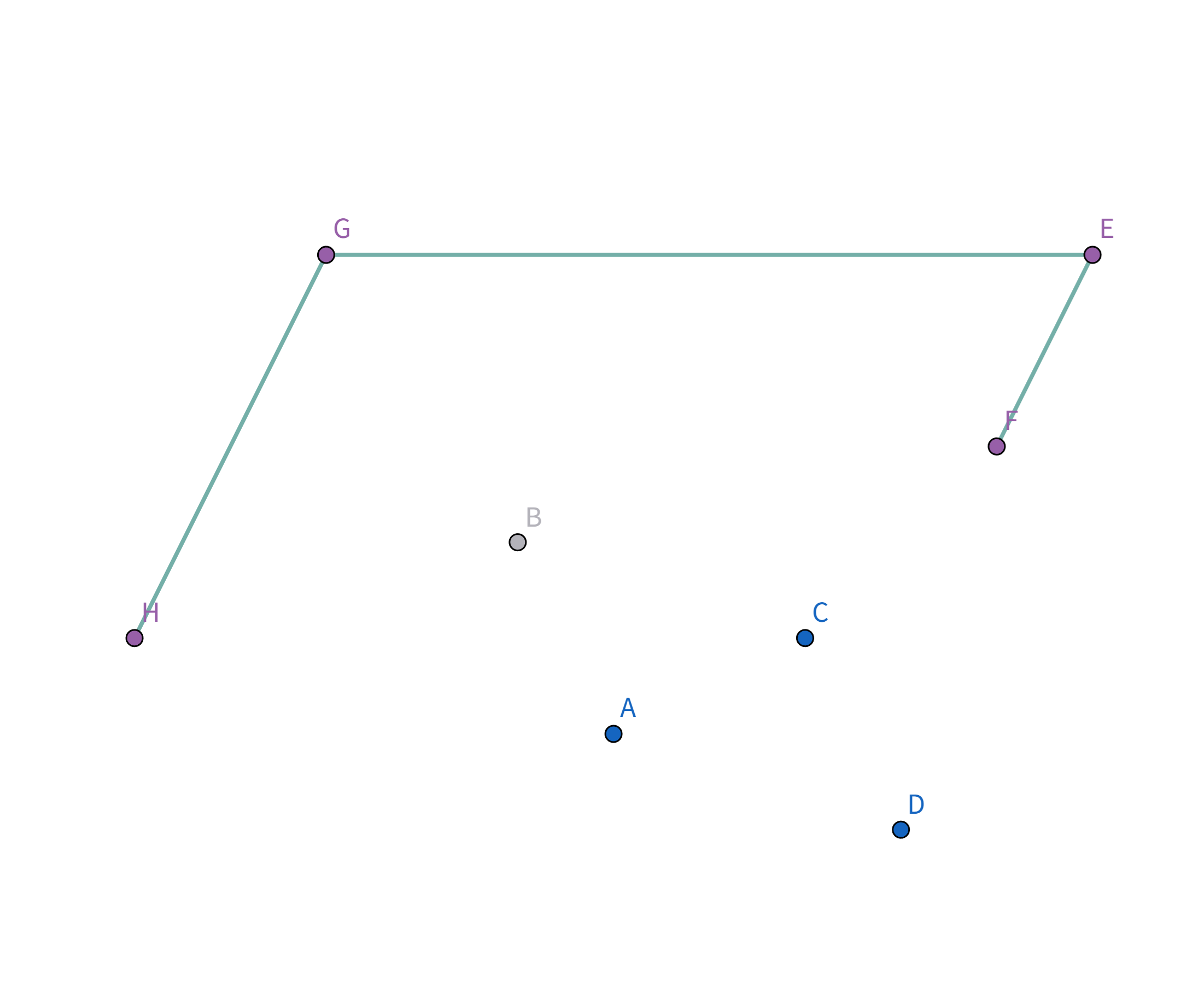
所以把点 $B$ 踢出栈,重复检查点 $F$ 和点 $E$ 的连线是否符合要求。发现其与栈顶的点 $E$ 连线的斜率 与之前的所有连线的斜率 满足递减关系,直接入栈:
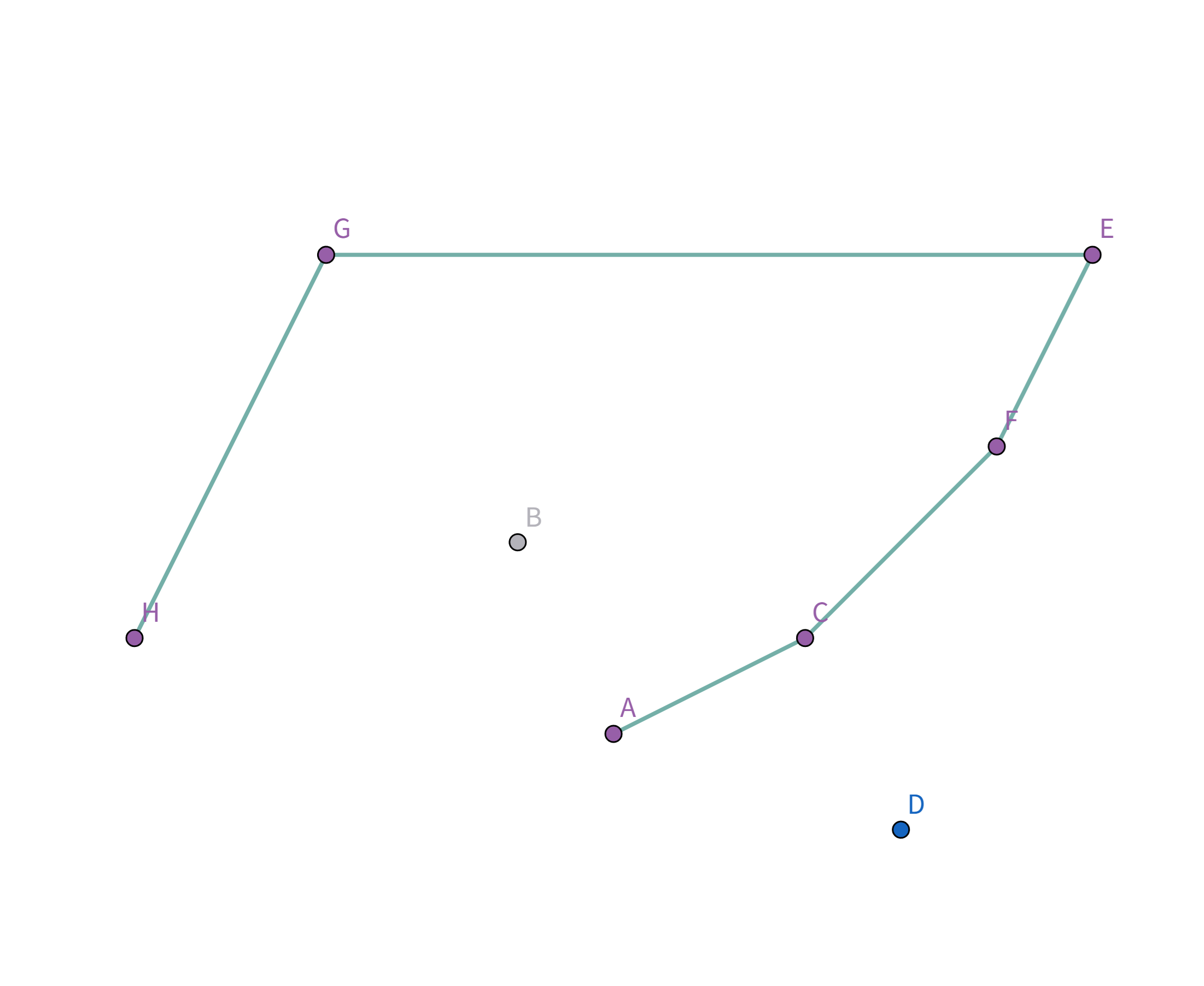
接着扫描到点 $C$,发现其与栈顶的点 $F$ 连线的斜率 与之前的所有连线的斜率 满足递减关系,直接入栈:
接着扫描到点 $A$,发现其与栈顶的点 $C$ 连线的斜率 与之前的所有连线的斜率 满足递减关系,直接入栈:
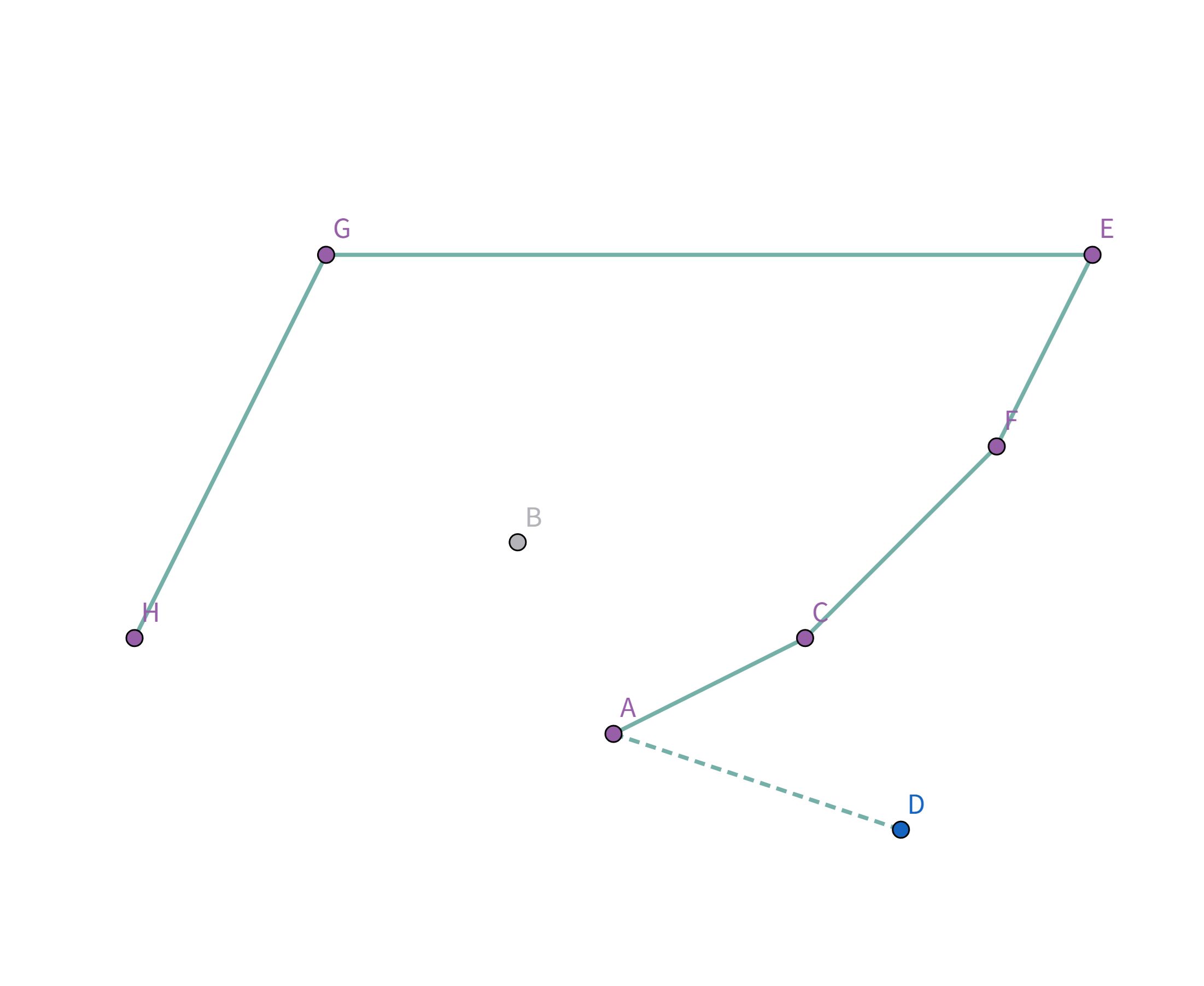
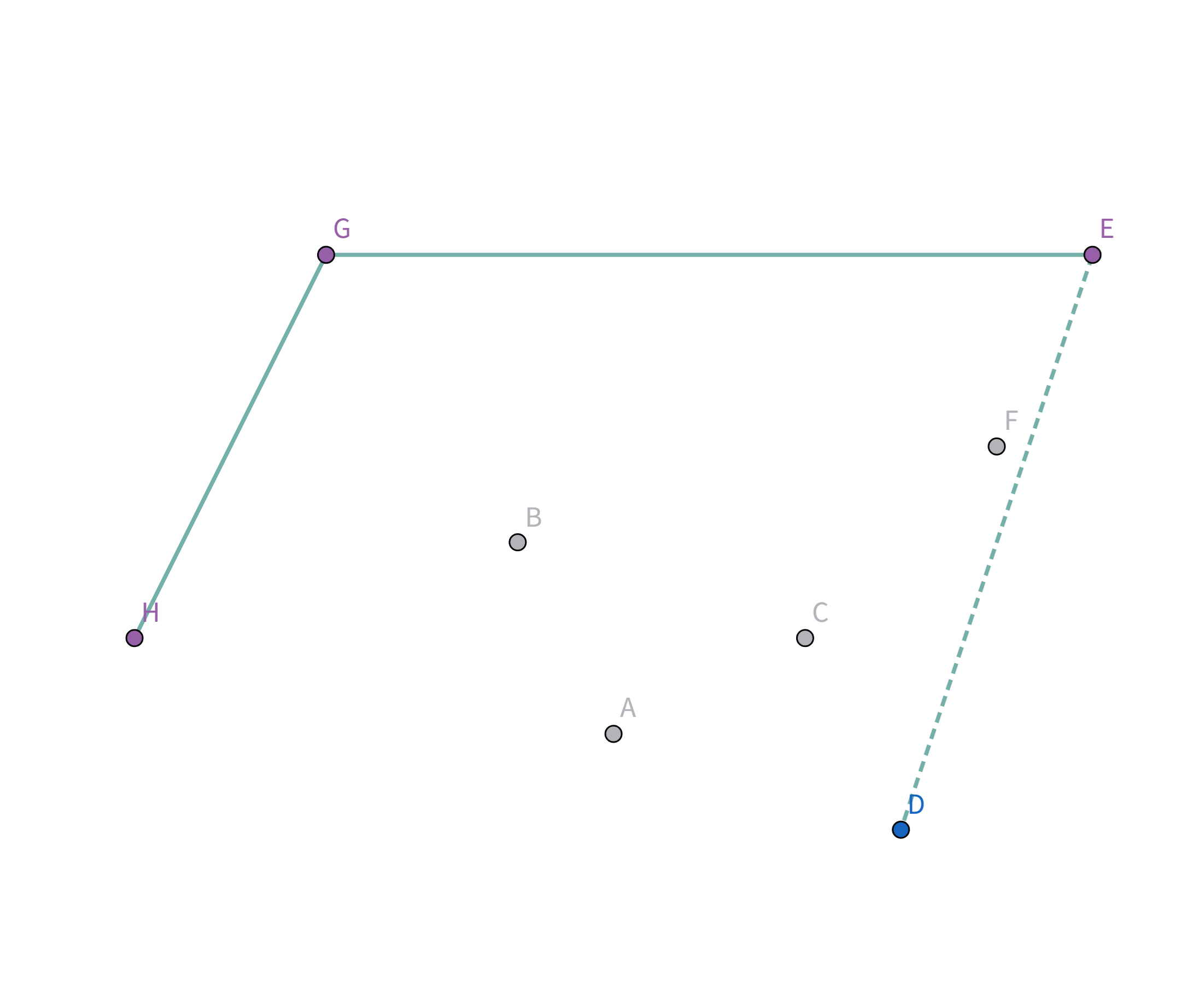
接着扫描到点 $D$!它与栈顶的点 $A$ 连线斜率比之前大!
所以把点 $A$ 踢出栈,重复检查点 $D$ 与栈顶点 $C$ 的连线,发现斜率仍然比之前大!
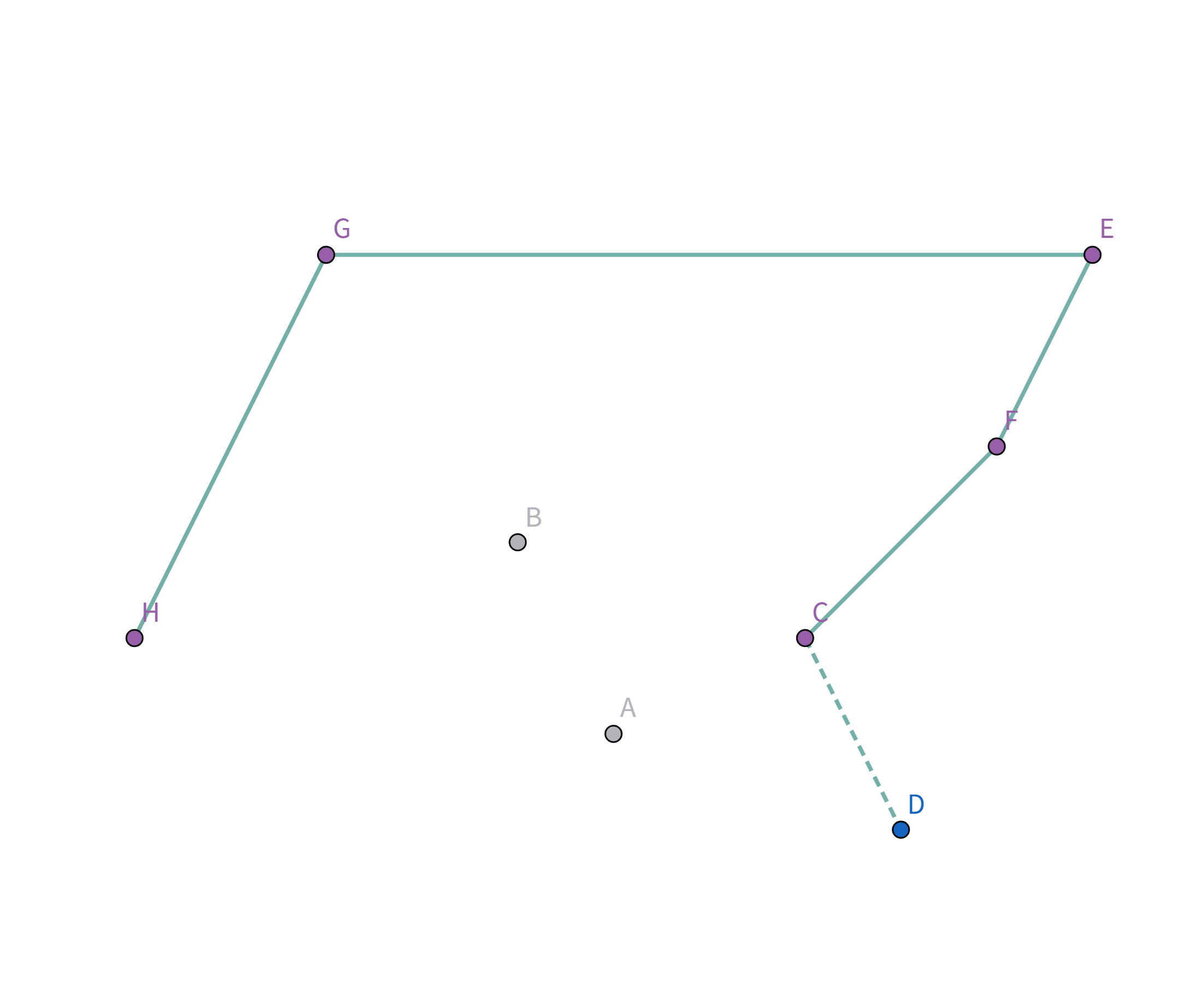
所以把点 $C$ 踢出栈,重复检查点 $D$ 与栈顶点 $F$ 的连线,发现斜率仍然比之前大!
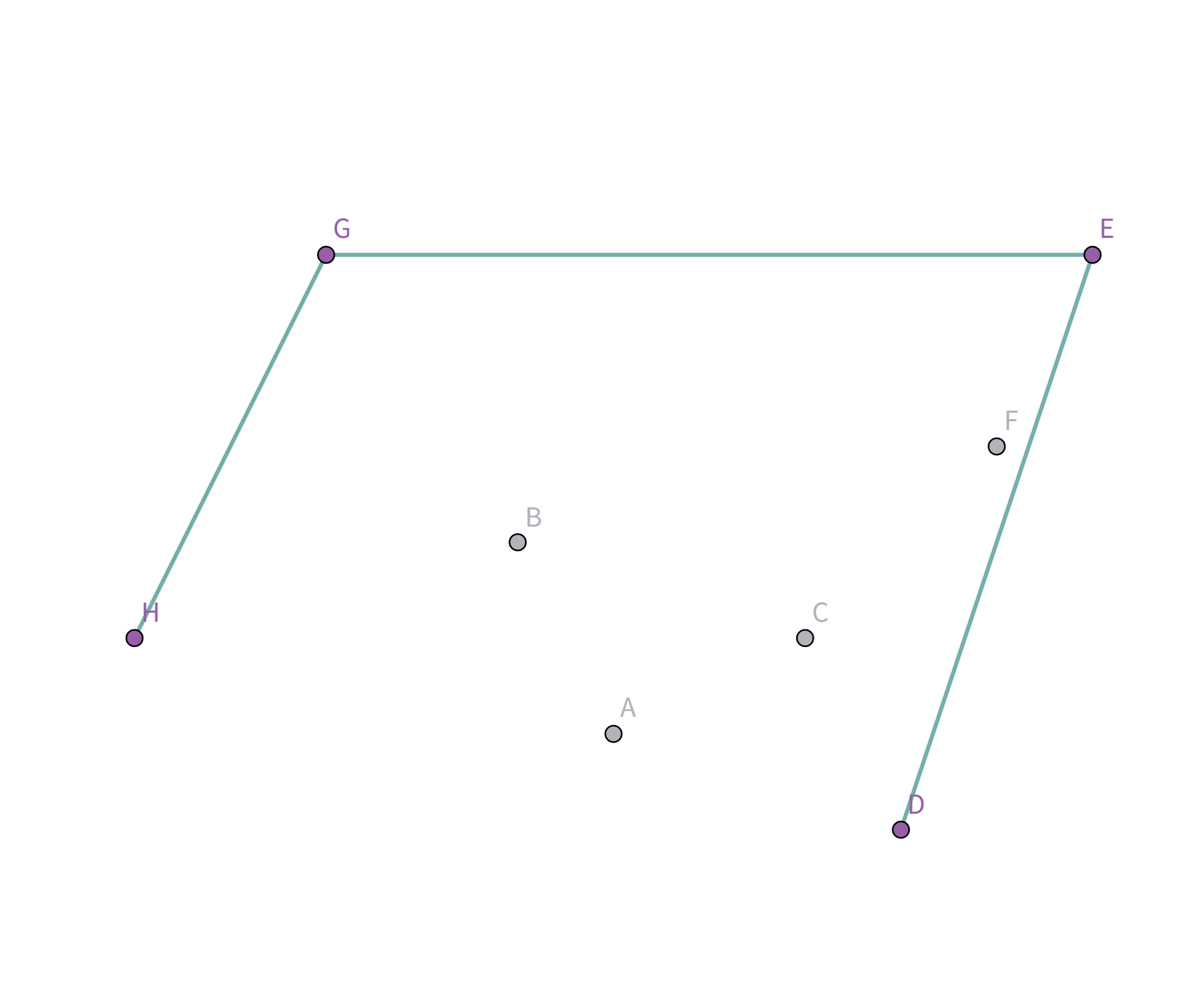
所以把点 $F$ 踢出栈,重复检查点 $D$ 与栈顶点 $E$ 的连线:
终于满足条件了!点 $D$ 与栈顶点 $E$ 连线的斜率 与之前所有连线的斜率 满足递减关系,所以入栈:
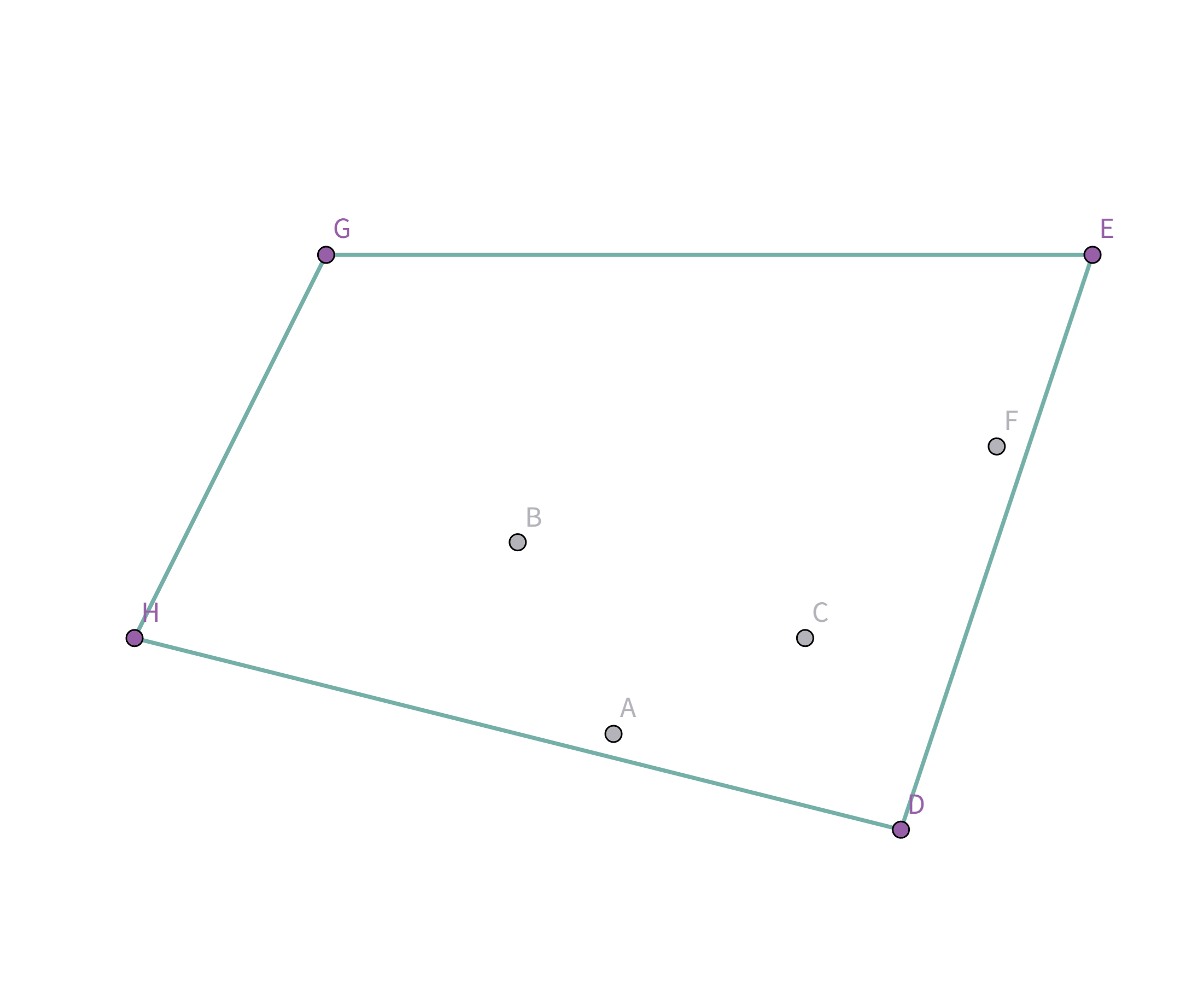
所有的点都扫描完啦!所以把最后的点 $D$ 和第一个点 $H$ 连上就好啦!
和前面的图一模一样哦!这个过程模拟就好啦! (其实判断斜率是否满足要求就看这些线段是不是一直在右转就好嘿嘿) NODE sta[MAXN]; int top;
int main() {
...
sta[++top] = node[1];
for (int i = 2; i <= n; ++i) {
while (top > 1 && !check(node[i], sta[top], sta[top], sta[top - 1])) top--;
sta[++top] = node[i];
}
...
}
此时,栈里面的元素就是要求的点集啦! 最后求花费不是难事: double dis(NODE x, NODE y) {
return sqrt(pow(x.x - y.x, 2) + pow(x.y - y.y, 2));
}
double ans;
int main() {
...
for (int i = 2; i <= top; ++i) {
ans += dis(sta[i], sta[i - 1]);
}
ans += dis(sta[top], sta[1]);
...
}
最终代码:
#include <cstdio>
#include <algorithm>
#include <cmath>
using ::std::sort;
using ::std::pow;
using ::std::sqrt;
const int MAXN = 1e5 + 10;
struct NODE {
double x, y;
} node[MAXN];
bool check(NODE a1, NODE a2, NODE b1, NODE b2) {
return (a1.y - a2.y) * (b1.x - b2.x) <= (b1.y - b2.y) * (a1.x - a2.x);
}
double dis(NODE x, NODE y) {
return sqrt(pow(x.x - y.x, 2) + pow(x.y - y.y, 2));
}
int n;
NODE sta[MAXN];
int top;
double ans;
int main() {
freopen("fc.in", "r", stdin);
freopen("fc.out", "w", stdout);
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%lf %lf", &node[i].x, &node[i].y);
}
sort(node + 1, node + n + 1, [](NODE x, NODE y) {
if (x.x != y.x) return x.x < y.x;
return x.y > y.y;
});
sort(node + 2, node + n + 1, [](NODE x, NODE y) {
return !check(x, node[1], y, node[1]);
});
sta[++top] = node[1];
for (int i = 2; i <= n; ++i) {
while (top > 1 && !check(node[i], sta[top], sta[top], sta[top - 1])) top--;
sta[++top] = node[i];
}
for (int i = 2; i <= top; ++i) {
ans += dis(sta[i], sta[i - 1]);
}
ans += dis(sta[top], sta[1]);
printf("%.2lf\n", ans);
return 0;
}
这个代码交到 COGS 上就能过啦!但是是错误的! HACK输入: 18 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 0 10 0 11 0 12 0 13 0 14 0 15 0 16 0 17 0 18输出: 48.00正确答案: 34.00出现这个问题的原因是所有的点出现在了同一条竖直的线上,数据范围超出了阈值,[code]::std::sort[/code] 函数选择使用快速排序,那么这些点原来按 $y$ 坐标降序的顺序就无法被保证,而这些点传入 [code]check[/code] 函数总是会返回 [code]true[/code],因为 [code]b1.x - b2.x[/code] 和 [code]a1.x - a2.x[/code] 都为 0。最终导致花费计算过多。
解决的办法是排序的时候加上特判。对于在同一条水平的线上的点也用同样的方法就好啦!
sort(node + 2, node + n + 1, [](NODE x, NODE y) {
if (x.x == node[1].x && y.x == node[1].x) return x.y > y.y; // 特判 x 坐标都一样
if (x.y == node[1].y && y.y == node[1].y) return x.x < y.x; // 特判 y 坐标都一样
return !check(x, node[1], y, node[1]);
});
最最终代码:
#include <cstdio>
#include <algorithm>
#include <cmath>
using ::std::sort;
using ::std::pow;
using ::std::sqrt;
const int MAXN = 1e5 + 10;
struct NODE {
double x, y;
} node[MAXN];
bool check(NODE a1, NODE a2, NODE b1, NODE b2) {
return (a1.y - a2.y) * (b1.x - b2.x) <= (b1.y - b2.y) * (a1.x - a2.x);
}
double dis(NODE x, NODE y) {
return sqrt(pow(x.x - y.x, 2) + pow(x.y - y.y, 2));
}
int n;
NODE sta[MAXN];
int top;
double ans;
int main() {
freopen("fc.in", "r", stdin);
freopen("fc.out", "w", stdout);
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%lf %lf", &node[i].x, &node[i].y);
}
sort(node + 1, node + n + 1, [](NODE x, NODE y) {
if (x.x != y.x) return x.x < y.x;
return x.y > y.y;
});
sort(node + 2, node + n + 1, [](NODE x, NODE y) {
if (x.x == node[1].x && y.x == node[1].x) return x.y > y.y;
if (x.y == node[1].y && y.y == node[1].y) return x.x < y.x;
return !check(x, node[1], y, node[1]);
});
sta[++top] = node[1];
for (int i = 2; i <= n; ++i) {
while (top > 1 && !check(node[i], sta[top], sta[top], sta[top - 1])) top--;
sta[++top] = node[i];
}
for (int i = 2; i <= top; ++i) {
ans += dis(sta[i], sta[i - 1]);
}
ans += dis(sta[top], sta[1]);
printf("%.2lf\n", ans);
return 0;
}
时间复杂度:$O(n \log{n} + n)$,瓶颈在排序。
|
|
|
Pro7 通信线路 题解通信线路 题解题目描述见 通信线路 整体思路只是一个最小生成树的模板题,数据量也没有很大 第一种方法:kruskal算法
两种实现:边集数组:时间复杂度$O(M log M + M(N + M))$; 第二种方法:Prim算法时间复杂度:$O(N^2)$(heap优化$O(M long M)$) 读者可以自行实现 代码实现最小生成树的两个主要算法都可以在讲义中找到,点击这个 本题解采用并查集 + kruskal 好孩子不可以抄代码哦 #include <bits/stdc++.h> // 万能头
using namespace std;
int n; // n是城市数
const int N = 1510,M = 1e4 + 10; // N是最大城市数,M是最大边数
struct Edge // 将边的参数定义到结构体里
{
int x,y,w; // x起点,y终点,w是权重
}e[M];
bool cmp(Edge &a,Edge &b) // 排序按照权重从小到大
{
return a.w < b.w;
}
int f[N]; // 并查集数组
void init()
{ // 并查集初始化
for(int i = 1; i <= N; ++i) f[i] = i;
}
int get(int x)
{ // 递归地查询x属于哪个集
if(x == f[x]) return x;
return f[x] = get(f[x]);
}
void merge(int x,int y)
{ // 将两个集合并
int fx = get(x),fy = get(y);
if(fx != fy) f[fy] = fx;
}
void kruskal()
{ // kruskal本体
init(); // 初始化
int ans = 0;
for(int i = 1;i <= M;i++)
{
int x = e[i].x,y = e[i].y,w = e[i].w; // 每次从边集中取出一个权重较小的
if(get(x) != get(y)) // 如果这条边的两个顶点不属于同一个集(就是不相连的意思)
{
merge(x,y); // 合并,即采用这条边
ans += w; // 总和记得加哦O(∩_∩)O
}
}
cout << ans << endl; // 输出就好乐,也可以返回ans在主函数里输出
}
int main()
{
freopen("mcst.in","r",stdin); // 文件输入输出
freopen("mcst.out","w",stdout);
cin >> n; // 输入城市数
int ind = 0;
for(int i = 0;i < n;i++)
{
for(int j = 0;j < n;j++)
{
int op; // 双重循环读入输入的矩阵(确信
cin >> op; // 第i+1个顶点到第j+1顶点之间边的权重
if(op != -1) e[ind].x = i + 1,e[ind].y = j + 1,e[ind].w = op,ind++;
// 如果两个顶点可以有边相连,就放在边集数组
}
}
sort(e,e+M,cmp); // 用cmp来排序
kruskal(); // kruskal,启动!
return 0; // 记得return是美德
}
|
|
|
×
提示!该题解未通过审核,建议分享者本着启发他人,照亮自己的初衷以图文并茂形式完善之,请勿粘贴代码。#include<iostream> using namespace std; int find(int x,int y,int n){ int num=x;
if(n-x+1<num) n 该题解等待再次审核........................................................................(剩余 790 个中英字符)
题目1811 [NOIP 2014PJ]螺旋矩阵
2025-05-10 07:27:49
|